
Previous in Relation and Functions Next in Relation and Functions
Question Number 42781 by maxmathsup by imad last updated on 02/Sep/18
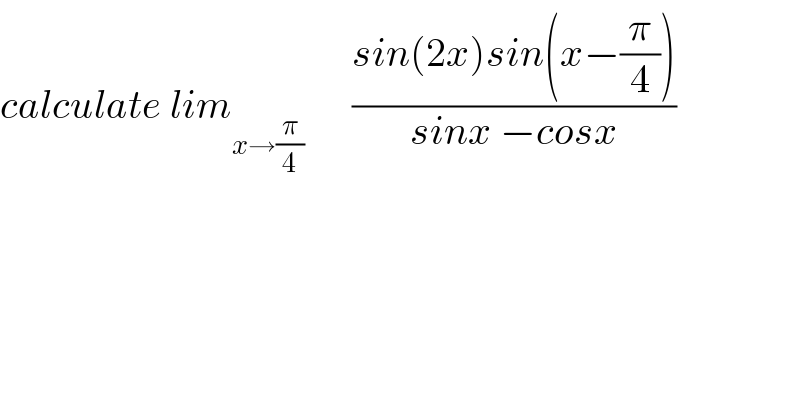
$${calculate}\:{lim}_{{x}\rightarrow\frac{\pi}{\mathrm{4}}} \:\:\:\:\:\:\frac{{sin}\left(\mathrm{2}{x}\right){sin}\left({x}−\frac{\pi}{\mathrm{4}}\right)}{{sinx}\:−{cosx}} \\ $$
Commented by maxmathsup by imad last updated on 04/Oct/18
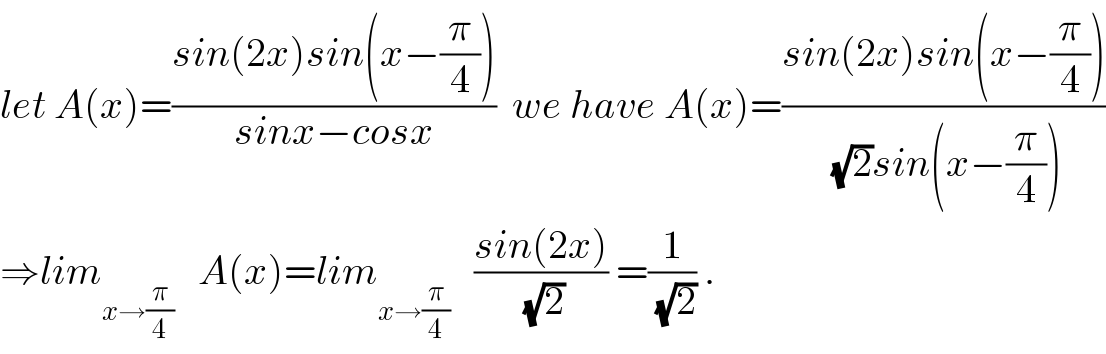
$${let}\:{A}\left({x}\right)=\frac{{sin}\left(\mathrm{2}{x}\right){sin}\left({x}−\frac{\pi}{\mathrm{4}}\right)}{{sinx}−{cosx}}\:\:{we}\:{have}\:{A}\left({x}\right)=\frac{{sin}\left(\mathrm{2}{x}\right){sin}\left({x}−\frac{\pi}{\mathrm{4}}\right)}{\sqrt{\mathrm{2}}{sin}\left({x}−\frac{\pi}{\mathrm{4}}\right)} \\ $$$$\Rightarrow{lim}_{{x}\rightarrow\frac{\pi}{\mathrm{4}}} \:\:\:{A}\left({x}\right)={lim}_{{x}\rightarrow\frac{\pi}{\mathrm{4}}} \:\:\:\frac{{sin}\left(\mathrm{2}{x}\right)}{\sqrt{\mathrm{2}}}\:=\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\:. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 03/Sep/18
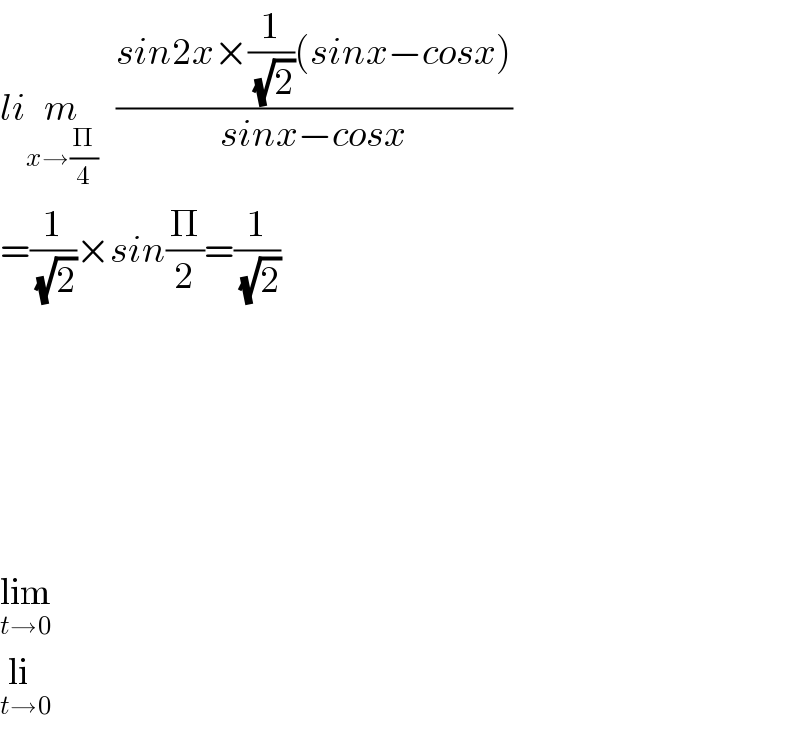
$${li}\underset{{x}\rightarrow\frac{\Pi}{\mathrm{4}}} {{m}}\:\:\:\frac{{sin}\mathrm{2}{x}×\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\left({sinx}−{cosx}\right)}{{sinx}−{cosx}} \\ $$$$=\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}×{sin}\frac{\Pi}{\mathrm{2}}=\frac{\mathrm{1}}{\sqrt{\mathrm{2}}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}} \\ $$$$\underset{{t}\rightarrow\mathrm{0}} {\mathrm{li}} \\ $$
