
Previous in Relation and Functions Next in Relation and Functions
Question Number 38641 by maxmathsup by imad last updated on 27/Jun/18
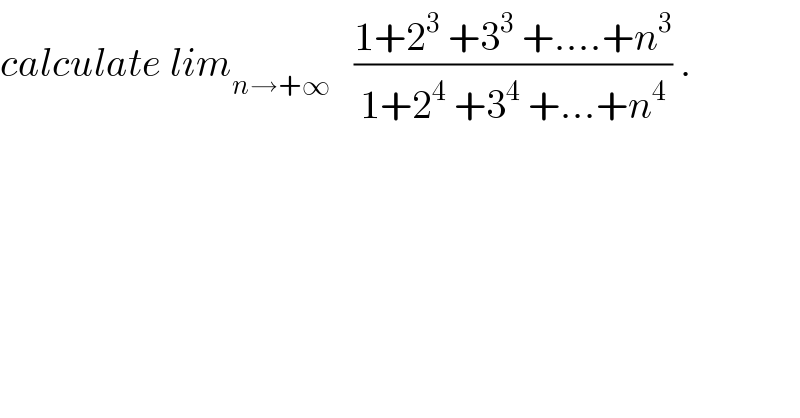
$${calculate}\:{lim}_{{n}\rightarrow+\infty} \:\:\:\frac{\mathrm{1}+\mathrm{2}^{\mathrm{3}} \:+\mathrm{3}^{\mathrm{3}} \:+....+{n}^{\mathrm{3}} }{\mathrm{1}+\mathrm{2}^{\mathrm{4}} \:+\mathrm{3}^{\mathrm{4}} \:+...+{n}^{\mathrm{4}} }\:. \\ $$
Commented by abdo mathsup 649 cc last updated on 28/Jun/18
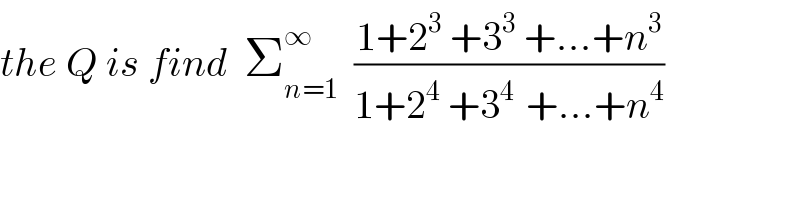
$${the}\:{Q}\:{is}\:{find}\:\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\mathrm{1}+\mathrm{2}^{\mathrm{3}} \:+\mathrm{3}^{\mathrm{3}} \:+...+{n}^{\mathrm{3}} }{\mathrm{1}+\mathrm{2}^{\mathrm{4}} \:+\mathrm{3}^{\mathrm{4}\:} \:+...+{n}^{\mathrm{4}} } \\ $$
