
Previous in Relation and Functions Next in Relation and Functions
Question Number 38642 by maxmathsup by imad last updated on 27/Jun/18
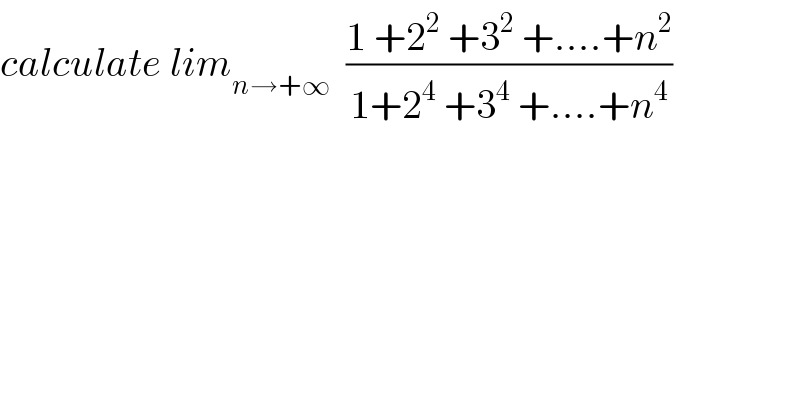
$${calculate}\:{lim}_{{n}\rightarrow+\infty} \:\:\frac{\mathrm{1}\:+\mathrm{2}^{\mathrm{2}} \:+\mathrm{3}^{\mathrm{2}} \:+....+{n}^{\mathrm{2}} }{\mathrm{1}+\mathrm{2}^{\mathrm{4}} \:+\mathrm{3}^{\mathrm{4}} \:+....+{n}^{\mathrm{4}} } \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 28/Jun/18
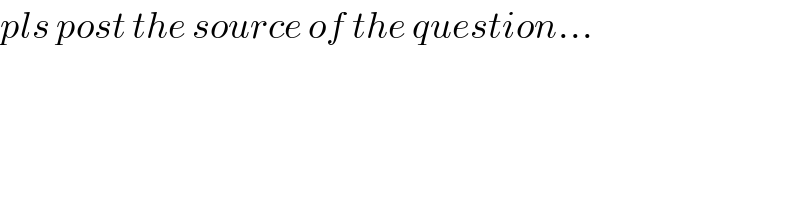
$${pls}\:{post}\:{the}\:{source}\:{of}\:{the}\:{question}... \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 28/Jun/18

$${i}\:{am}\:{not}\:{solving}\:{the}\:{question}\:{but}\:{putting} \\ $$$${simple}\:{logic} \\ $$$$\mathrm{2}^{\mathrm{4}} >\mathrm{2}^{\mathrm{2}} \\ $$$$\mathrm{3}^{\mathrm{4}} >\mathrm{3}^{\mathrm{2}} \\ $$$${thus}\:\underset{\mathrm{1}} {\overset{{n}} {\sum}}{r}^{\mathrm{4}} \:>\underset{\mathrm{1}} {\overset{{n}} {\sum}}{r}^{\mathrm{2}} \\ $$$${so}\:{D}_{{r}} >>{N}_{{r}} \\ $$$${when}\:\:{n}\rightarrow\infty\:\:{i}\:{think}\:\:{limit}\:{value}\:\rightarrow\mathrm{0} \\ $$$${so}\:{pls}\:{comment}\:{whether}\:{i}\:{am}\:{right}\:{or}\:{wrong} \\ $$$${also}\:{solve}\:{atleast}\:{one}\:{question}\:{to}\:{KNOW} \\ $$$${THE}\:{UNKNOWN}... \\ $$
Commented by abdo mathsup 649 cc last updated on 28/Jun/18
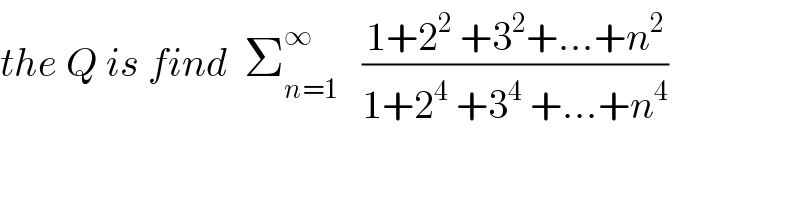
$${the}\:{Q}\:{is}\:{find}\:\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\frac{\mathrm{1}+\mathrm{2}^{\mathrm{2}} \:+\mathrm{3}^{\mathrm{2}} +...+{n}^{\mathrm{2}} }{\mathrm{1}+\mathrm{2}^{\mathrm{4}} \:+\mathrm{3}^{\mathrm{4}} \:+...+{n}^{\mathrm{4}} } \\ $$
