
Question Number 62412 by mathmax by abdo last updated on 20/Jun/19
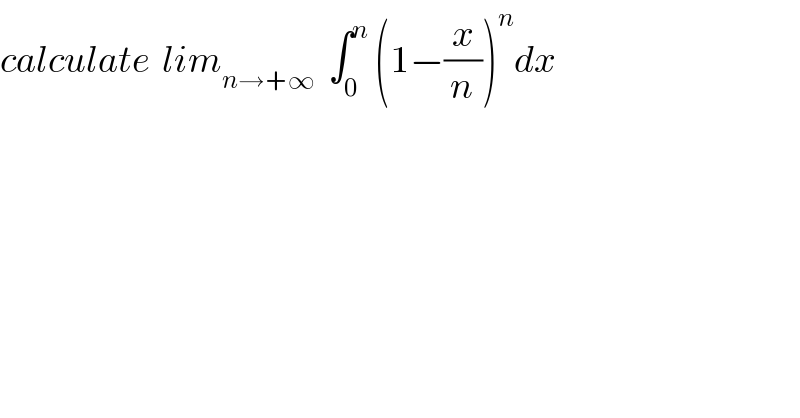
$${calculate}\:\:{lim}_{{n}\rightarrow+\infty} \:\:\int_{\mathrm{0}} ^{{n}} \:\left(\mathrm{1}−\frac{{x}}{{n}}\right)^{{n}} {dx} \\ $$
Commented by mathmax by abdo last updated on 03/Jul/19
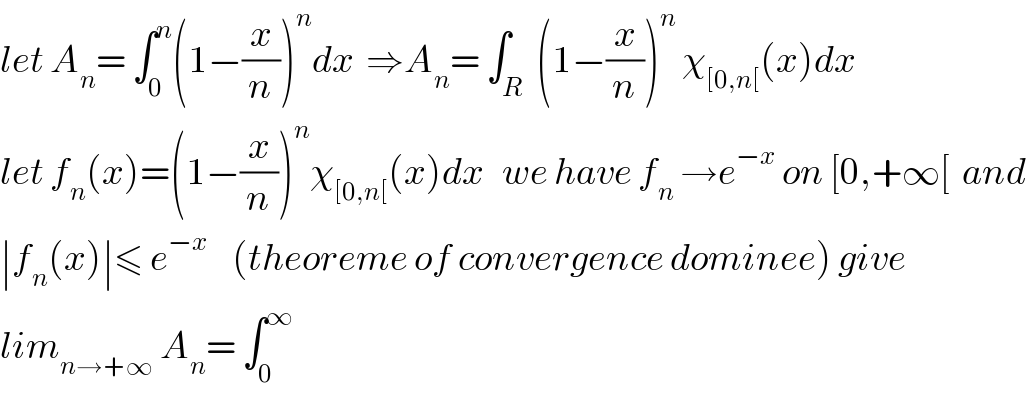
$${let}\:{A}_{{n}} =\:\int_{\mathrm{0}} ^{{n}} \left(\mathrm{1}−\frac{{x}}{{n}}\right)^{{n}} {dx}\:\:\Rightarrow{A}_{{n}} =\:\int_{{R}} \:\left(\mathrm{1}−\frac{{x}}{{n}}\right)^{{n}} \:\chi_{\left[\mathrm{0},{n}\left[\right.\right.} \left({x}\right){dx} \\ $$$${let}\:{f}_{{n}} \left({x}\right)=\left(\mathrm{1}−\frac{{x}}{{n}}\right)^{{n}} \chi_{\left[\mathrm{0},{n}\left[\right.\right.} \left({x}\right){dx}\:\:\:{we}\:{have}\:{f}_{{n}} \:\rightarrow{e}^{−{x}} \:{on}\:\left[\mathrm{0},+\infty\left[\:\:{and}\right.\right. \\ $$$$\mid{f}_{{n}} \left({x}\right)\mid\leqslant\:{e}^{−{x}} \:\:\:\:\left({theoreme}\:{of}\:{convergence}\:{dominee}\right)\:{give} \\ $$$${lim}_{{n}\rightarrow+\infty} \:{A}_{{n}} =\:\int_{\mathrm{0}} ^{\infty} \\ $$
Commented by mathmax by abdo last updated on 03/Jul/19
![lim_(n→+∞) A_n =∫_R lim_(n→+∞) f_n (x)dx =∫_0 ^∞ e^(−x) dx =[−e^(−x) ]_0 ^(+∞) =1](Q63402.png)
$${lim}_{{n}\rightarrow+\infty} \:{A}_{{n}} =\int_{{R}} {lim}_{{n}\rightarrow+\infty} \:{f}_{{n}} \left({x}\right){dx}\:=\int_{\mathrm{0}} ^{\infty} \:{e}^{−{x}} {dx}\:=\left[−{e}^{−{x}} \right]_{\mathrm{0}} ^{+\infty} \:=\mathrm{1} \\ $$
