Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 46607 by maxmathsup by imad last updated on 29/Oct/18

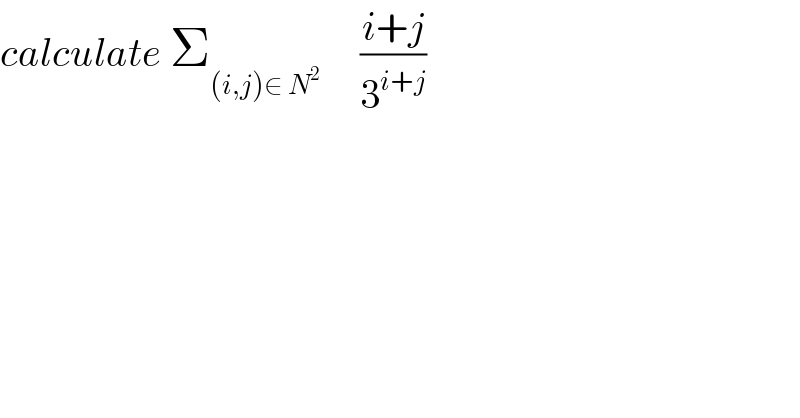
calculate Σ_((i,j)∈ N^2 ) ((i+j)/3^(i+j) )

$${calculate}\:\sum_{\left({i},{j}\right)\in\:{N}^{\mathrm{2}} } \:\:\:\:\:\frac{{i}+{j}}{\mathrm{3}^{{i}+{j}} } \\ $$

Commented by maxmathsup by imad last updated on 30/Oct/18

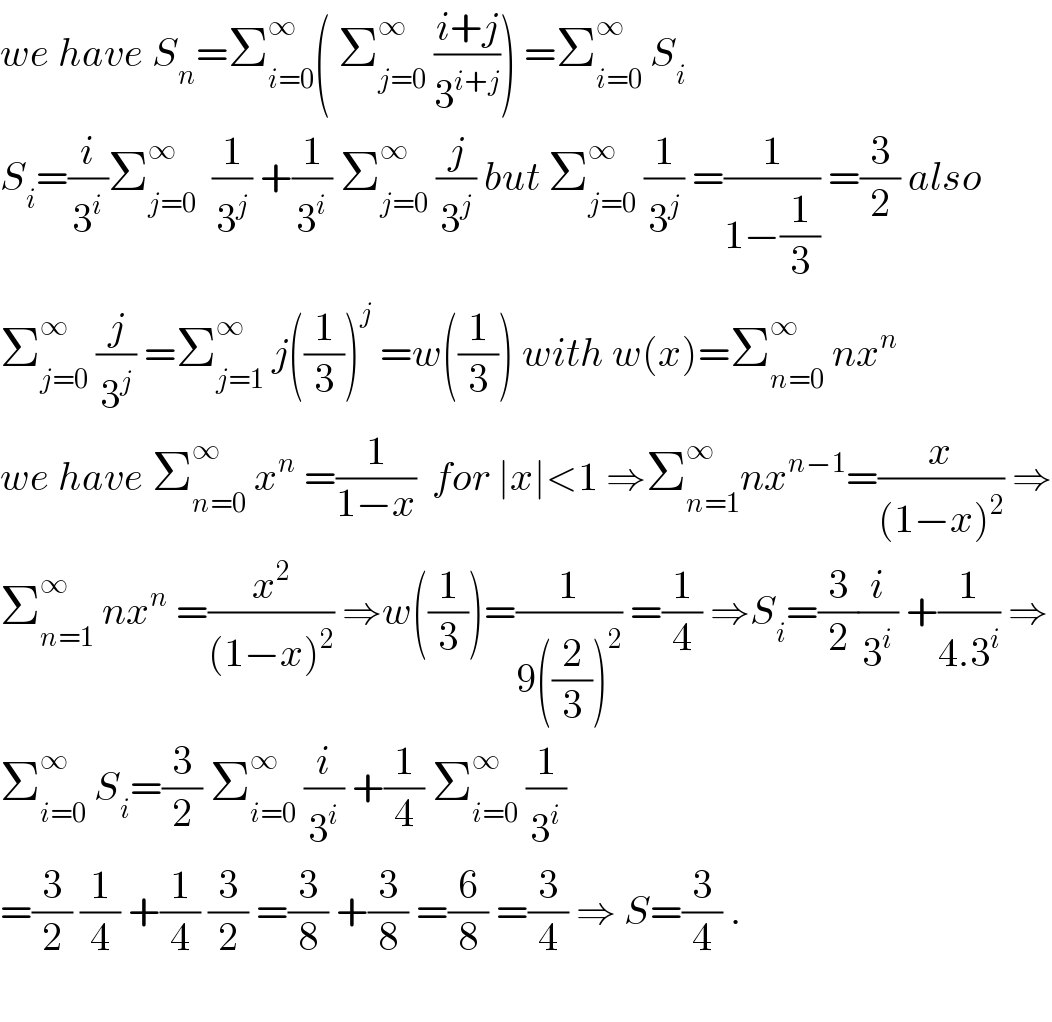
we have S_n =Σ_(i=0) ^∞ ( Σ_(j=0) ^∞ ((i+j)/3^(i+j) )) =Σ_(i=0) ^∞ S_i S_i =(i/3^i )Σ_(j=0) ^∞ (1/3^j ) +(1/3^i ) Σ_(j=0) ^∞ (j/3^j ) but Σ_(j=0) ^∞ (1/3^j ) =(1/(1−(1/3))) =(3/2) also Σ_(j=0) ^∞ (j/3^j ) =Σ_(j=1) ^∞ j((1/3))^j =w((1/3)) with w(x)=Σ_(n=0) ^∞ nx^n we have Σ_(n=0) ^∞ x^n =(1/(1−x)) for ∣x∣<1 ⇒Σ_(n=1) ^∞ nx^(n−1) =(x/((1−x)^2 )) ⇒ Σ_(n=1) ^∞ nx^n =(x^2 /((1−x)^2 )) ⇒w((1/3))=(1/(9((2/3))^2 )) =(1/4) ⇒S_i =(3/2)(i/3^i ) +(1/(4.3^i )) ⇒ Σ_(i=0) ^∞ S_i =(3/2) Σ_(i=0) ^∞ (i/3^i ) +(1/4) Σ_(i=0) ^∞ (1/3^i ) =(3/2) (1/4) +(1/4) (3/2) =(3/8) +(3/8) =(6/8) =(3/4) ⇒ S=(3/4) .

$${we}\:{have}\:{S}_{{n}} =\sum_{{i}=\mathrm{0}} ^{\infty} \left(\:\sum_{{j}=\mathrm{0}} ^{\infty} \:\frac{{i}+{j}}{\mathrm{3}^{{i}+{j}} }\right)\:=\sum_{{i}=\mathrm{0}} ^{\infty} \:{S}_{{i}} \\ $$$${S}_{{i}} =\frac{{i}}{\mathrm{3}^{{i}} }\sum_{{j}=\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}}{\mathrm{3}^{{j}} }\:+\frac{\mathrm{1}}{\mathrm{3}^{{i}} }\:\sum_{{j}=\mathrm{0}} ^{\infty} \:\frac{{j}}{\mathrm{3}^{{j}} }\:{but}\:\sum_{{j}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{3}^{{j}} }\:=\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}}\:=\frac{\mathrm{3}}{\mathrm{2}}\:{also} \\ $$$$\sum_{{j}=\mathrm{0}} ^{\infty} \:\frac{{j}}{\mathrm{3}^{{j}} }\:=\sum_{{j}=\mathrm{1}} ^{\infty} \:{j}\left(\frac{\mathrm{1}}{\mathrm{3}}\right)^{{j}} \:={w}\left(\frac{\mathrm{1}}{\mathrm{3}}\right)\:{with}\:{w}\left({x}\right)=\sum_{{n}=\mathrm{0}} ^{\infty} \:{nx}^{{n}} \\ $$$${we}\:{have}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:{x}^{{n}} \:=\frac{\mathrm{1}}{\mathrm{1}−{x}}\:\:{for}\:\mid{x}\mid<\mathrm{1}\:\Rightarrow\sum_{{n}=\mathrm{1}} ^{\infty} {nx}^{{n}−\mathrm{1}} =\frac{{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:{nx}^{{n}} \:=\frac{{x}^{\mathrm{2}} }{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }\:\Rightarrow{w}\left(\frac{\mathrm{1}}{\mathrm{3}}\right)=\frac{\mathrm{1}}{\mathrm{9}\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow{S}_{{i}} =\frac{\mathrm{3}}{\mathrm{2}}\frac{{i}}{\mathrm{3}^{{i}} }\:+\frac{\mathrm{1}}{\mathrm{4}.\mathrm{3}^{{i}} }\:\Rightarrow \\ $$$$\sum_{{i}=\mathrm{0}} ^{\infty} \:{S}_{{i}} =\frac{\mathrm{3}}{\mathrm{2}}\:\sum_{{i}=\mathrm{0}} ^{\infty} \:\frac{{i}}{\mathrm{3}^{{i}} }\:+\frac{\mathrm{1}}{\mathrm{4}}\:\sum_{{i}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{3}^{{i}} } \\ $$$$=\frac{\mathrm{3}}{\mathrm{2}}\:\frac{\mathrm{1}}{\mathrm{4}}\:+\frac{\mathrm{1}}{\mathrm{4}}\:\frac{\mathrm{3}}{\mathrm{2}}\:=\frac{\mathrm{3}}{\mathrm{8}}\:+\frac{\mathrm{3}}{\mathrm{8}}\:=\frac{\mathrm{6}}{\mathrm{8}}\:=\frac{\mathrm{3}}{\mathrm{4}}\:\Rightarrow\:{S}=\frac{\mathrm{3}}{\mathrm{4}}\:. \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com