
Question Number 67850 by mathmax by abdo last updated on 01/Sep/19
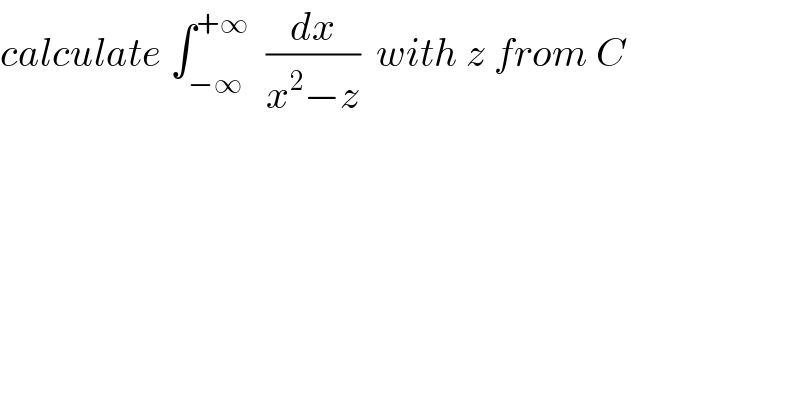
$${calculate}\:\int_{−\infty} ^{+\infty} \:\:\frac{{dx}}{{x}^{\mathrm{2}} −{z}}\:\:{with}\:{z}\:{from}\:{C} \\ $$
Commented by mathmax by abdo last updated on 01/Sep/19

$${let}\:{I}\:=\int_{−\infty} ^{+\infty} \:\frac{{dx}}{{x}^{\mathrm{2}} −{z}}\:\:{let}\:{z}\:={re}^{{i}\theta} \:\Rightarrow{I}\:=\int_{−\infty} ^{+\infty} \:\frac{{dx}}{{x}^{\mathrm{2}} −\left(\sqrt{{r}}{e}^{\frac{{i}\theta}{\mathrm{2}}} \right)^{\mathrm{2}} } \\ $$$$=\int_{−\infty} ^{+\infty} \:\:\frac{{dx}}{\left({x}−\sqrt{{r}}{e}^{\frac{{i}\theta}{\mathrm{2}}} \right)\left({x}+\sqrt{{r}}{e}^{\frac{{i}\theta}{\mathrm{2}}} \right)}\:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{{r}}{e}^{\frac{{i}\theta}{\mathrm{2}}} }\int_{−\infty} ^{+\infty} \left\{\frac{\mathrm{1}}{{x}−\sqrt{{r}}{e}^{\frac{{i}\theta}{\mathrm{2}}} }−\frac{\mathrm{1}}{{x}+\sqrt{{r}}{e}^{\frac{{i}\theta}{\mathrm{2}}} }\right\}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{{r}}{e}^{\frac{{i}\theta}{\mathrm{2}}} }\left\{\:\int_{−\infty} ^{+\infty} \:\frac{{dx}}{{x}−\sqrt{{r}}{e}^{\frac{{i}\theta}{\mathrm{2}}} }\:−\int_{−\infty} ^{+\infty} \:\frac{{dx}}{{x}−\left(−\sqrt{{r}}{e}^{\frac{{i}\theta}{\mathrm{2}}} \right)}\right\} \\ $$$${we}\:{have}\:{proved}\:{that}\:{for}\:{a}\:\in{C}\:\:\int_{−\infty} ^{+\infty} \:\frac{{dx}}{{x}−{a}}\:={i}\pi\:{if}\:{Im}\left({a}\right)>\mathrm{0}\:{and} \\ $$$$−{i}\pi\:{if}\:{Im}\left({a}\right)<\mathrm{0}\:{so}\:\:{if}\:\theta>\mathrm{0}\:\Rightarrow \\ $$$${I}\:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{{r}}{e}^{\frac{{i}\theta}{\mathrm{2}}} }\left\{{i}\pi−\left(−{i}\pi\right)\right\}\:=\frac{\mathrm{2}{i}\pi}{\mathrm{2}\sqrt{{r}}{e}^{\frac{{i}\theta}{\mathrm{2}}} }\:=\frac{{i}\pi}{\sqrt{{r}}{e}^{\frac{{i}\theta}{\mathrm{2}}} } \\ $$$${if}\:\theta<\mathrm{0}\:\:{weget}\:\:{I}\:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{{r}}{e}^{\frac{{i}\theta}{\mathrm{2}}} }\left\{−{i}\pi−\left({i}\pi\right)\right\}\:=−\frac{{i}\pi}{\sqrt{{r}}{e}^{\frac{{i}\theta}{\mathrm{2}}} } \\ $$
