
Question Number 64150 by mathmax by abdo last updated on 14/Jul/19
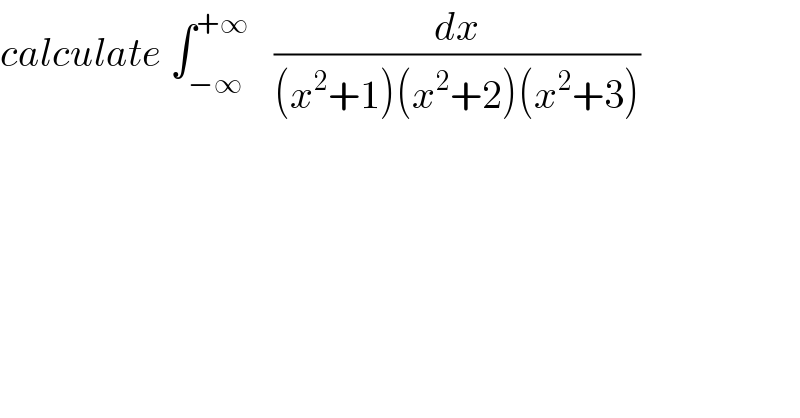
$${calculate}\:\int_{−\infty} ^{+\infty} \:\:\:\frac{{dx}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{2}\right)\left({x}^{\mathrm{2}} +\mathrm{3}\right)} \\ $$
Commented by mathmax by abdo last updated on 14/Jul/19

$${residus}\:{method}\:{let}\:{f}\left({z}\right)=\frac{\mathrm{1}}{\left({z}^{\mathrm{2}} +\mathrm{1}\right)\left({z}^{\mathrm{2}} \:+\mathrm{2}\right)\left({z}^{\mathrm{2}} \:+\mathrm{3}\right)} \\ $$$${we}\:{have}\:{f}\left({z}\right)\:=\frac{\mathrm{1}}{\left({z}−{i}\right)\left({z}+{i}\right)\left({z}−{i}\sqrt{\mathrm{2}}\right)\left({z}+{i}\sqrt{\mathrm{2}}\right)\left({z}−{i}\sqrt{\mathrm{3}}\right)\left({z}+{i}\sqrt{\mathrm{3}}\right)} \\ $$$${so}\:{the}\:{poles}\:{of}\:{f}\:{are}\:\overset{−} {+}{i}\:,\overset{−} {+}{i}\sqrt{\mathrm{2}}{and}\:\overset{−} {+}{i}\sqrt{\mathrm{3}}\:\:\:{residus}\:{theorem}\:{give} \\ $$$$\left.\int_{−\infty} ^{+\infty} {f}−{z}\right){dz}\:=\mathrm{2}{i}\pi\:\left\{{Res}\left({f},{i}\right)+{Res}\left({f},{i}\sqrt{\mathrm{2}}\right)\:+{Res}\left({f},{i}\sqrt{\mathrm{3}}\right)\right\} \\ $$$${Res}\left({f},{i}\right)\:={lim}_{{z}\rightarrow{i}} \left({z}−{i}\right){f}\left({z}\right)\:=\frac{\mathrm{1}}{\mathrm{2}{i}\left(−\mathrm{1}+\mathrm{2}\right)\left(−\mathrm{1}+\mathrm{3}\right)}\:=\frac{\mathrm{1}}{\mathrm{4}{i}} \\ $$$${Res}\left({f},{i}\sqrt{\mathrm{2}}\right)={lim}_{{z}\rightarrow{i}\sqrt{\mathrm{2}}} \:\:\left({z}−{i}\sqrt{\mathrm{2}}\right){f}\left({z}\right)\:=\frac{\mathrm{1}}{\mathrm{2}{i}\sqrt{\mathrm{2}}\left(−\mathrm{2}+\mathrm{1}\right)\left(−\mathrm{2}+\mathrm{3}\right)} \\ $$$$=\frac{\mathrm{1}}{−\mathrm{2}{i}\sqrt{\mathrm{2}}} \\ $$$${Res}\left({f},{i}\sqrt{\mathrm{3}}\right)\:={lim}_{{z}\rightarrow{i}\sqrt{\mathrm{3}}} \:\:\:\left({z}−{i}\sqrt{\mathrm{3}}\right){f}\left({z}\right)=\frac{\mathrm{1}}{\mathrm{2}{i}\sqrt{\mathrm{3}}\left(−\mathrm{3}+\mathrm{1}\right)\left(−\mathrm{3}+\mathrm{2}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}{i}\sqrt{\mathrm{3}}}\:\Rightarrow\int_{−\infty} ^{+\infty} {f}\left({z}\right){dz}\:=\mathrm{2}{i}\pi\left\{\frac{\mathrm{1}}{\mathrm{4}{i}}\:−\frac{\mathrm{1}}{\mathrm{2}{i}\sqrt{\mathrm{2}}}\:+\frac{\mathrm{1}}{\mathrm{4}{i}\sqrt{\mathrm{3}}}\right\} \\ $$$$=\frac{\pi}{\mathrm{2}}\:−\frac{\pi}{\sqrt{\mathrm{2}}}\:+\frac{\pi}{\mathrm{2}\sqrt{\mathrm{3}}}\:\:\Rightarrow\:{I}\:=\frac{\pi}{\mathrm{2}}\:−\frac{\pi}{\sqrt{\mathrm{2}}}\:+\frac{\pi}{\sqrt{\mathrm{3}}}\:. \\ $$
Commented by mathmax by abdo last updated on 14/Jul/19
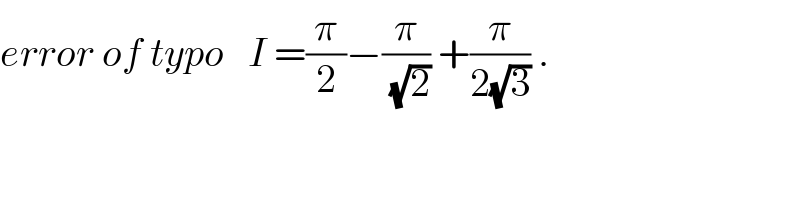
$${error}\:{of}\:{typo}\:\:\:{I}\:=\frac{\pi}{\mathrm{2}}−\frac{\pi}{\sqrt{\mathrm{2}}}\:+\frac{\pi}{\mathrm{2}\sqrt{\mathrm{3}}}\:. \\ $$
Answered by ajfour last updated on 14/Jul/19
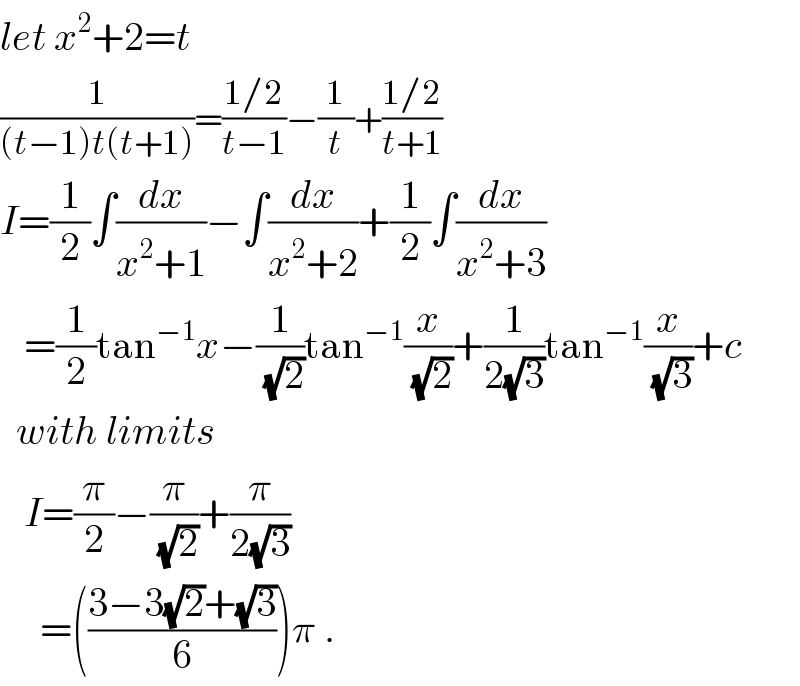
$${let}\:{x}^{\mathrm{2}} +\mathrm{2}={t} \\ $$$$\frac{\mathrm{1}}{\left({t}−\mathrm{1}\right){t}\left({t}+\mathrm{1}\right)}=\frac{\mathrm{1}/\mathrm{2}}{{t}−\mathrm{1}}−\frac{\mathrm{1}}{{t}}+\frac{\mathrm{1}/\mathrm{2}}{{t}+\mathrm{1}} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dx}}{{x}^{\mathrm{2}} +\mathrm{1}}−\int\frac{{dx}}{{x}^{\mathrm{2}} +\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dx}}{{x}^{\mathrm{2}} +\mathrm{3}} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{tan}^{−\mathrm{1}} {x}−\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\mathrm{tan}^{−\mathrm{1}} \frac{{x}}{\sqrt{\mathrm{2}}}+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}\mathrm{tan}^{−\mathrm{1}} \frac{{x}}{\sqrt{\mathrm{3}}}+{c} \\ $$$$\:\:{with}\:{limits} \\ $$$$\:\:\:{I}=\frac{\pi}{\mathrm{2}}−\frac{\pi}{\sqrt{\mathrm{2}}}+\frac{\pi}{\mathrm{2}\sqrt{\mathrm{3}}} \\ $$$$\:\:\:\:\:=\left(\frac{\mathrm{3}−\mathrm{3}\sqrt{\mathrm{2}}+\sqrt{\mathrm{3}}}{\mathrm{6}}\right)\pi\:. \\ $$
Commented by mathmax by abdo last updated on 14/Jul/19
$${thank}\:{you}\:{sir}\:{ajfour}\:{your}\:{answer}\:{is}\:{correct}. \\ $$
