Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 63721 by mathmax by abdo last updated on 08/Jul/19

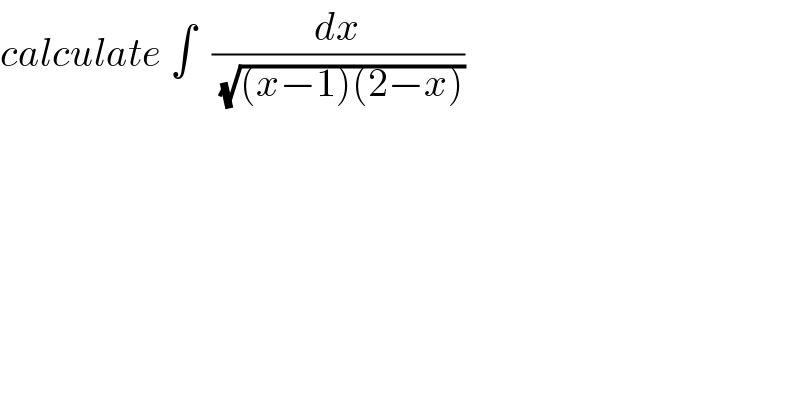
calculate ∫ (dx/(√((x−1)(2−x))))

$${calculate}\:\int\:\:\frac{{dx}}{\sqrt{\left({x}−\mathrm{1}\right)\left(\mathrm{2}−{x}\right)}} \\ $$

Commented by Prithwish sen last updated on 08/Jul/19

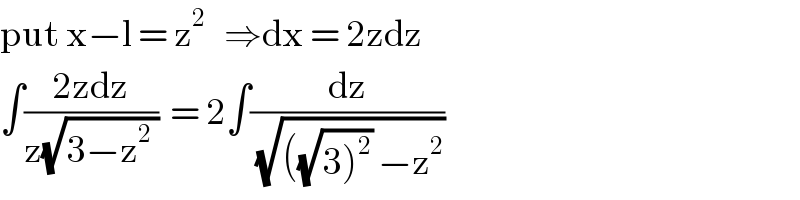
put x−l = z^2 ⇒dx = 2zdz ∫((2zdz)/(z(√(3−z^2 )))) = 2∫(dz/(√(((√(3)^2 )) −z^2 )))

$$\mathrm{put}\:\mathrm{x}−\mathrm{l}\:=\:\mathrm{z}^{\mathrm{2}} \:\:\:\Rightarrow\mathrm{dx}\:=\:\mathrm{2zdz} \\ $$$$\int\frac{\mathrm{2zdz}}{\mathrm{z}\sqrt{\mathrm{3}−\mathrm{z}^{\mathrm{2}} \:}}\:\:=\:\mathrm{2}\int\frac{\mathrm{dz}}{\sqrt{\left(\sqrt{\left.\mathrm{3}\right)^{\mathrm{2}} }\:−\mathrm{z}^{\mathrm{2}} \right.}}\:\:\:\: \\ $$

Commented by mathmax by abdo last updated on 08/Jul/19

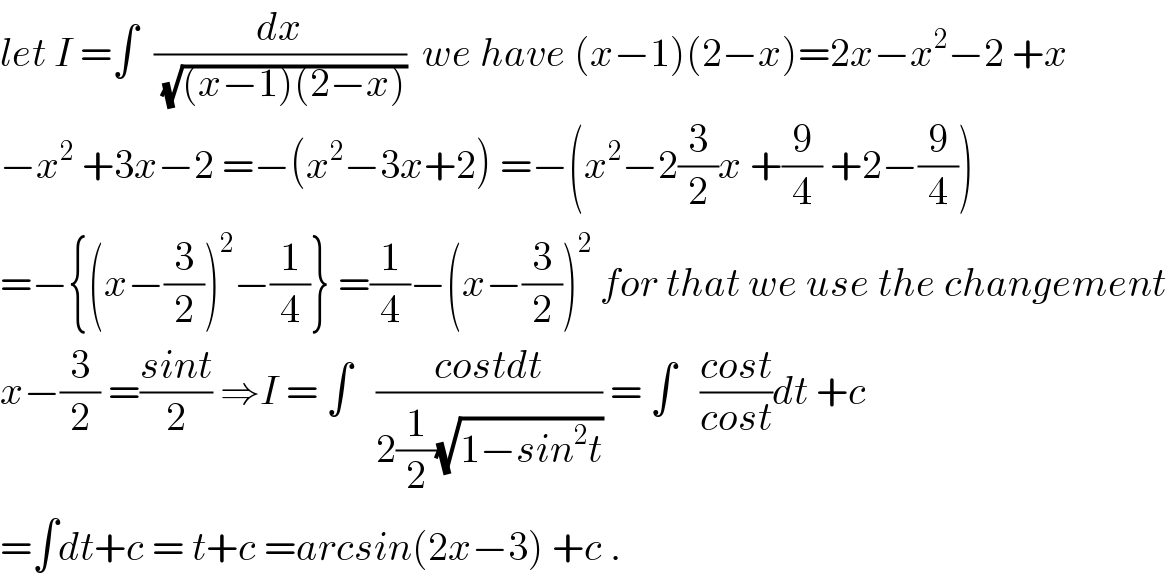
let I =∫ (dx/(√((x−1)(2−x)))) we have (x−1)(2−x)=2x−x^2 −2 +x −x^2 +3x−2 =−(x^2 −3x+2) =−(x^2 −2(3/2)x +(9/4) +2−(9/4)) =−{(x−(3/2))^2 −(1/4)} =(1/4)−(x−(3/2))^2 for that we use the changement x−(3/2) =((sint)/2) ⇒I = ∫ ((costdt)/(2(1/2)(√(1−sin^2 t)))) = ∫ ((cost)/(cost))dt +c =∫dt+c = t+c =arcsin(2x−3) +c .

$${let}\:{I}\:=\int\:\:\frac{{dx}}{\sqrt{\left({x}−\mathrm{1}\right)\left(\mathrm{2}−{x}\right)}}\:\:{we}\:{have}\:\left({x}−\mathrm{1}\right)\left(\mathrm{2}−{x}\right)=\mathrm{2}{x}−{x}^{\mathrm{2}} −\mathrm{2}\:+{x} \\ $$$$−{x}^{\mathrm{2}} \:+\mathrm{3}{x}−\mathrm{2}\:=−\left({x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{2}\right)\:=−\left({x}^{\mathrm{2}} −\mathrm{2}\frac{\mathrm{3}}{\mathrm{2}}{x}\:+\frac{\mathrm{9}}{\mathrm{4}}\:+\mathrm{2}−\frac{\mathrm{9}}{\mathrm{4}}\right) \\ $$$$=−\left\{\left({x}−\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}\right\}\:=\frac{\mathrm{1}}{\mathrm{4}}−\left({x}−\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} \:{for}\:{that}\:{we}\:{use}\:{the}\:{changement} \\ $$$${x}−\frac{\mathrm{3}}{\mathrm{2}}\:=\frac{{sint}}{\mathrm{2}}\:\Rightarrow{I}\:=\:\int\:\:\:\frac{{costdt}}{\mathrm{2}\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{1}−{sin}^{\mathrm{2}} {t}}}\:=\:\int\:\:\:\frac{{cost}}{{cost}}{dt}\:+{c} \\ $$$$=\int{dt}+{c}\:=\:{t}+{c}\:={arcsin}\left(\mathrm{2}{x}−\mathrm{3}\right)\:+{c}\:. \\ $$

Answered by MJS last updated on 08/Jul/19

∫(dx/(√((x−1)(2−x))))= [t=arccos (2x−3) → dx=−(√((x−1)(2−x)))dt] =−∫dt=−t=−arccos (2x−3) +C

$$\int\frac{{dx}}{\sqrt{\left({x}−\mathrm{1}\right)\left(\mathrm{2}−{x}\right)}}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{arccos}\:\left(\mathrm{2}{x}−\mathrm{3}\right)\:\rightarrow\:{dx}=−\sqrt{\left({x}−\mathrm{1}\right)\left(\mathrm{2}−{x}\right)}{dt}\right] \\ $$$$=−\int{dt}=−{t}=−\mathrm{arccos}\:\left(\mathrm{2}{x}−\mathrm{3}\right)\:+{C} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com