Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 32715 by caravan msup abdo. last updated on 31/Mar/18

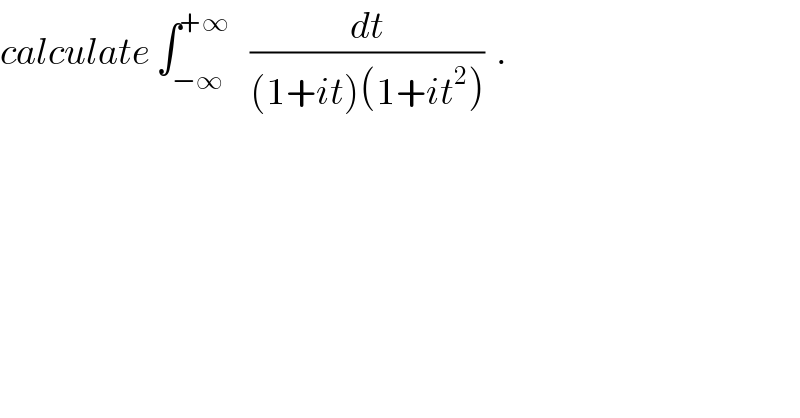
calculate ∫_(−∞) ^(+∞) (dt/((1+it)(1+it^2 ))) .

$${calculate}\:\int_{−\infty} ^{+\infty} \:\:\:\frac{{dt}}{\left(\mathrm{1}+{it}\right)\left(\mathrm{1}+{it}^{\mathrm{2}} \right)}\:\:. \\ $$

Commented by abdo imad last updated on 03/Apr/18

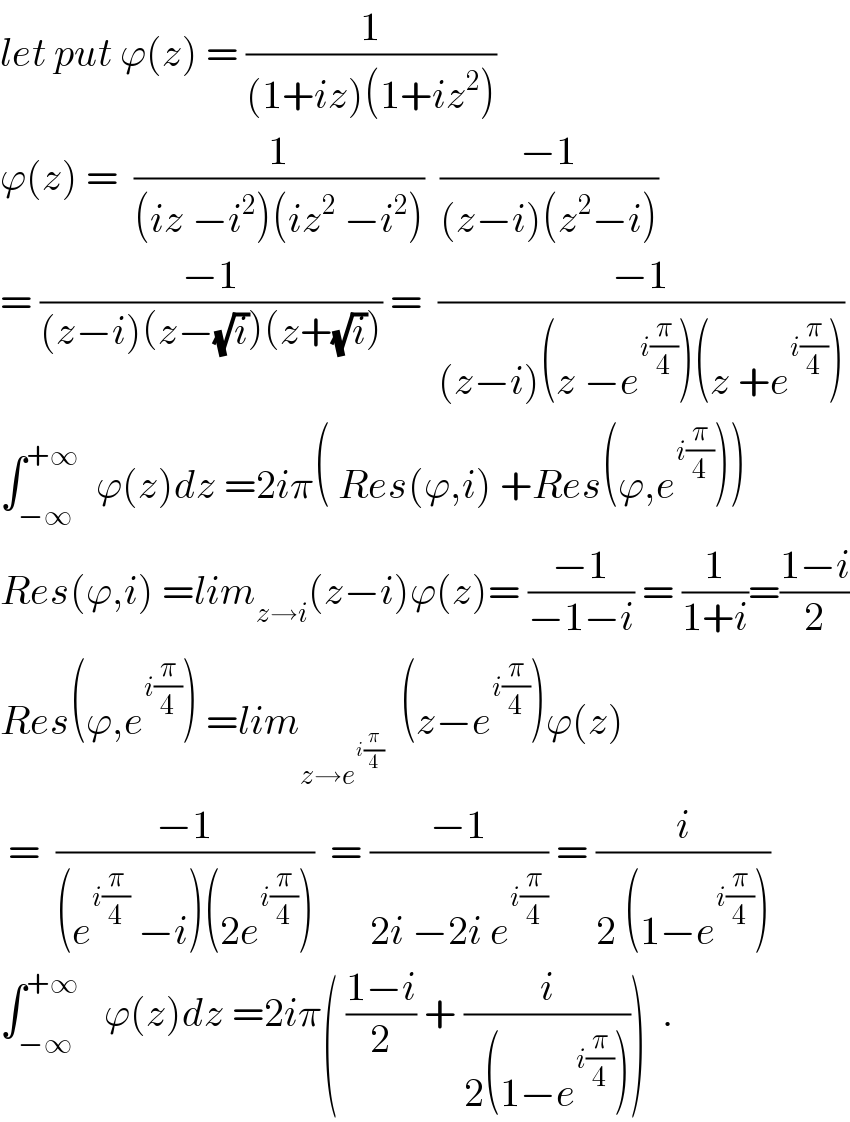
let put ϕ(z) = (1/((1+iz)(1+iz^2 ))) ϕ(z) = (1/((iz −i^2 )(iz^2 −i^2 ))) ((−1)/((z−i)(z^2 −i))) = ((−1)/((z−i)(z−(√i))(z+(√i)))) = ((−1)/((z−i)(z −e^(i(π/4)) )(z +e^(i(π/4)) ))) ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ( Res(ϕ,i) +Res(ϕ,e^(i(π/4)) )) Res(ϕ,i) =lim_(z→i) (z−i)ϕ(z)= ((−1)/(−1−i)) = (1/(1+i))=((1−i)/2) Res(ϕ,e^(i(π/4)) ) =lim_(z→e^(i(π/4)) ) (z−e^(i(π/4)) )ϕ(z) = ((−1)/((e^(i(π/4)) −i)(2e^(i(π/4)) ))) = ((−1)/(2i −2i e^(i(π/4)) )) = (i/(2 (1−e^(i(π/4)) ))) ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ( ((1−i)/2) + (i/(2(1−e^(i(π/4)) )))) .

$${let}\:{put}\:\varphi\left({z}\right)\:=\:\frac{\mathrm{1}}{\left(\mathrm{1}+{iz}\right)\left(\mathrm{1}+{iz}^{\mathrm{2}} \right)} \\ $$$$\varphi\left({z}\right)\:=\:\:\frac{\mathrm{1}}{\left({iz}\:−{i}^{\mathrm{2}} \right)\left({iz}^{\mathrm{2}} \:−{i}^{\mathrm{2}} \right)}\:\:\frac{−\mathrm{1}}{\left({z}−{i}\right)\left({z}^{\mathrm{2}} −{i}\right)} \\ $$$$=\:\frac{−\mathrm{1}}{\left({z}−{i}\right)\left({z}−\sqrt{{i}}\right)\left({z}+\sqrt{{i}}\right)}\:=\:\:\frac{−\mathrm{1}}{\left({z}−{i}\right)\left({z}\:−{e}^{{i}\frac{\pi}{\mathrm{4}}} \right)\left({z}\:+{e}^{{i}\frac{\pi}{\mathrm{4}}} \right)} \\ $$$$\int_{−\infty} ^{+\infty} \:\:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\left(\:{Res}\left(\varphi,{i}\right)\:+{Res}\left(\varphi,{e}^{{i}\frac{\pi}{\mathrm{4}}} \right)\right) \\ $$$${Res}\left(\varphi,{i}\right)\:={lim}_{{z}\rightarrow{i}} \left({z}−{i}\right)\varphi\left({z}\right)=\:\frac{−\mathrm{1}}{−\mathrm{1}−{i}}\:=\:\frac{\mathrm{1}}{\mathrm{1}+{i}}=\frac{\mathrm{1}−{i}}{\mathrm{2}} \\ $$$${Res}\left(\varphi,{e}^{{i}\frac{\pi}{\mathrm{4}}} \right)\:={lim}_{{z}\rightarrow{e}^{{i}\frac{\pi}{\mathrm{4}}} } \:\:\left({z}−{e}^{{i}\frac{\pi}{\mathrm{4}}} \right)\varphi\left({z}\right) \\ $$$$\:=\:\:\frac{−\mathrm{1}}{\left({e}^{{i}\frac{\pi}{\mathrm{4}}} \:−{i}\right)\left(\mathrm{2}{e}^{{i}\frac{\pi}{\mathrm{4}}} \right)}\:\:=\:\frac{−\mathrm{1}}{\mathrm{2}{i}\:−\mathrm{2}{i}\:{e}^{{i}\frac{\pi}{\mathrm{4}}} }\:=\:\frac{{i}}{\mathrm{2}\:\left(\mathrm{1}−{e}^{{i}\frac{\pi}{\mathrm{4}}} \right)} \\ $$$$\int_{−\infty} ^{+\infty} \:\:\:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\left(\:\frac{\mathrm{1}−{i}}{\mathrm{2}}\:+\:\frac{{i}}{\mathrm{2}\left(\mathrm{1}−{e}^{{i}\frac{\pi}{\mathrm{4}}} \right)}\right)\:\:. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com