
Question Number 217219 by mnjuly1970 last updated on 06/Mar/25
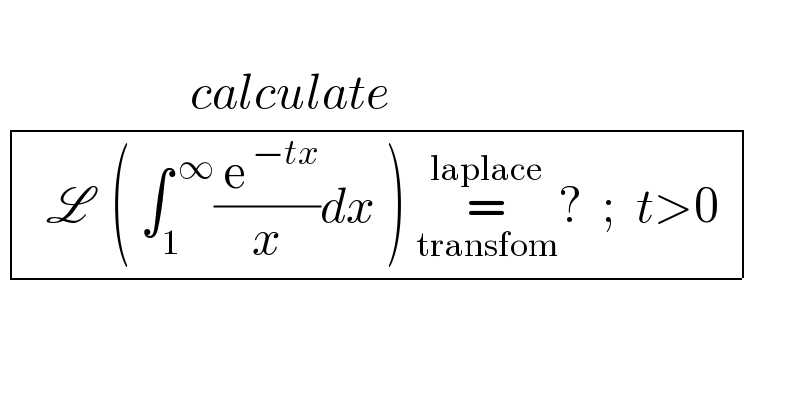
$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{calculate} \\ $$$$\begin{array}{|c|}{\:\:\mathscr{L}\:\:\left(\:\int_{\mathrm{1}} ^{\:\infty} \frac{\:\mathrm{e}^{\:−{tx}} }{{x}}{dx}\:\right)\:\underset{\mathrm{transfom}} {\overset{\mathrm{laplace}} {=}}?\:\:;\:\:{t}>\mathrm{0}\:}\\\hline\end{array} \\ $$$$ \\ $$$$\:\:\: \\ $$
Answered by Wuji last updated on 06/Mar/25
![f(t)=∫_1 ^∞ (e^(−tx) /x)dx , t>0 u=tx ⇒dx=(1/t)du ; x=(u/t) f(t)=∫_t ^∞ (e^(−u) /(u/t))•(1/t)du =∫_t ^∞ (e^(−u) /u)du=E_1 (t) f(t)=E_1 (t) L{f}(s) =∫_0 ^∞ e^(−st) E_1 (t) L{f}(s)=∫_0 ^∞ e^(−st) [∫_0 ^∞ (e^(−tx) /x)dx]dt =∫_1 ^∞ (1/x)[∫_0 ^∞ e^(−t(s+x)) dt]dx ∫_0 ^∞ e^(−t(s+x)) dt=(1/(s+x)) {∀R(s+x) >0} L{f}(s)=∫_1 ^∞ (1/(x(s+x)))dx (1/(x(s+x)))=(1/s)((1/x)−(1/(s+x))) L{f}(s)=(1/s)∫_1 ^∞ (1/x)dx−∫_1 ^∞ (1/(s+x))dx ∫_1 ^R (1/x)dx =ln(R) ; ∫^R _1 (2/(s+x))dx=∫_(s+1) ^(s+R) (1/u)du=ln(s+R)−ln(s+1) ∫_1 ^R (1/x)dx−∫_1 ^R (1/(s+x))dx=ln(R)−[ln(s+R)−ln(s+1)]=ln(((R(s+1))/((s+R)))) ((R(s+1))/((s+R))) → s+1 ln(s+1) ∴L{f}(s)=(1/s)ln(s+1) f(t)=∫_0 ^∞ (e^(−tx) /x)dt=(1/s)ln(s+1)](Q217231.png)
$$\mathrm{f}\left(\mathrm{t}\right)=\overset{\infty} {\int}_{\mathrm{1}} \frac{\mathrm{e}^{−\mathrm{tx}} }{\mathrm{x}}\mathrm{dx}\:\:\:\:\:\:\:,\:\mathrm{t}>\mathrm{0} \\ $$$$\mathrm{u}=\mathrm{tx}\:\:\Rightarrow\mathrm{dx}=\frac{\mathrm{1}}{\mathrm{t}}\mathrm{du}\:\:;\:\mathrm{x}=\frac{\mathrm{u}}{\mathrm{t}} \\ $$$$\mathrm{f}\left(\mathrm{t}\right)=\int_{\mathrm{t}} ^{\infty} \frac{\mathrm{e}^{−\mathrm{u}} }{\frac{\mathrm{u}}{\mathrm{t}}}\bullet\frac{\mathrm{1}}{\mathrm{t}}\mathrm{du}\:=\int_{\mathrm{t}} ^{\infty} \frac{\mathrm{e}^{−\mathrm{u}} }{\mathrm{u}}\mathrm{du}=\mathrm{E}_{\mathrm{1}} \left(\mathrm{t}\right) \\ $$$$\mathrm{f}\left(\mathrm{t}\right)=\mathrm{E}_{\mathrm{1}} \left(\mathrm{t}\right) \\ $$$$\mathscr{L}\left\{\mathrm{f}\right\}\left(\mathrm{s}\right)\:=\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\mathrm{st}} \mathrm{E}_{\mathrm{1}} \left(\mathrm{t}\right) \\ $$$$\mathscr{L}\left\{\mathrm{f}\right\}\left(\mathrm{s}\right)=\underset{\mathrm{0}} {\overset{\infty} {\int}}\mathrm{e}^{−\mathrm{st}} \left[\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{\mathrm{e}^{−\mathrm{tx}} }{\mathrm{x}}\mathrm{dx}\right]\mathrm{dt} \\ $$$$=\underset{\mathrm{1}} {\overset{\infty} {\int}}\frac{\mathrm{1}}{\mathrm{x}}\left[\overset{\infty} {\int}_{\mathrm{0}} \mathrm{e}^{−\mathrm{t}\left(\mathrm{s}+\mathrm{x}\right)} \mathrm{dt}\right]\mathrm{dx} \\ $$$$\underset{\mathrm{0}} {\overset{\infty} {\int}}\mathrm{e}^{−\mathrm{t}\left(\mathrm{s}+\mathrm{x}\right)} \mathrm{dt}=\frac{\mathrm{1}}{\mathrm{s}+\mathrm{x}}\:\:\:\:\:\:\left\{\forall\mathbb{R}\left(\mathrm{s}+\mathrm{x}\right)\:\:>\mathrm{0}\right\} \\ $$$$\mathscr{L}\left\{\mathrm{f}\right\}\left(\mathrm{s}\right)=\int_{\mathrm{1}} ^{\infty} \frac{\mathrm{1}}{\mathrm{x}\left(\mathrm{s}+\mathrm{x}\right)}\mathrm{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{x}\left(\mathrm{s}+\mathrm{x}\right)}=\frac{\mathrm{1}}{\mathrm{s}}\left(\frac{\mathrm{1}}{\mathrm{x}}−\frac{\mathrm{1}}{\mathrm{s}+\mathrm{x}}\right) \\ $$$$\mathscr{L}\left\{\mathrm{f}\right\}\left(\mathrm{s}\right)=\frac{\mathrm{1}}{\mathrm{s}}\underset{\mathrm{1}} {\overset{\infty} {\int}}\frac{\mathrm{1}}{\mathrm{x}}\mathrm{dx}−\underset{\mathrm{1}} {\overset{\infty} {\int}}\frac{\mathrm{1}}{\mathrm{s}+\mathrm{x}}\mathrm{dx} \\ $$$$\underset{\mathrm{1}} {\overset{\mathrm{R}} {\int}}\frac{\mathrm{1}}{\mathrm{x}}\mathrm{dx}\:=\mathrm{ln}\left(\mathrm{R}\right)\:\:;\:\underset{\mathrm{1}} {\int}^{\mathrm{R}} \frac{\mathrm{2}}{\mathrm{s}+\mathrm{x}}\mathrm{dx}=\underset{\mathrm{s}+\mathrm{1}} {\overset{\mathrm{s}+\mathrm{R}} {\int}}\frac{\mathrm{1}}{\mathrm{u}}\mathrm{du}=\mathrm{ln}\left(\mathrm{s}+\mathrm{R}\right)−\mathrm{ln}\left(\mathrm{s}+\mathrm{1}\right) \\ $$$$\underset{\mathrm{1}} {\overset{\mathrm{R}} {\int}}\frac{\mathrm{1}}{\mathrm{x}}\mathrm{dx}−\underset{\mathrm{1}} {\overset{\mathrm{R}} {\int}}\frac{\mathrm{1}}{\mathrm{s}+\mathrm{x}}\mathrm{dx}=\mathrm{ln}\left(\mathrm{R}\right)−\left[\mathrm{ln}\left(\mathrm{s}+\mathrm{R}\right)−\mathrm{ln}\left(\mathrm{s}+\mathrm{1}\right)\right]=\mathrm{ln}\left(\frac{\mathrm{R}\left(\mathrm{s}+\mathrm{1}\right)}{\left(\mathrm{s}+\mathrm{R}\right)}\right) \\ $$$$\frac{\mathrm{R}\left(\mathrm{s}+\mathrm{1}\right)}{\left(\mathrm{s}+\mathrm{R}\right)}\:\rightarrow\:\mathrm{s}+\mathrm{1} \\ $$$$\mathrm{ln}\left(\mathrm{s}+\mathrm{1}\right) \\ $$$$\therefore\mathscr{L}\left\{\mathrm{f}\right\}\left(\mathrm{s}\right)=\frac{\mathrm{1}}{\mathrm{s}}\mathrm{ln}\left(\mathrm{s}+\mathrm{1}\right) \\ $$$$\mathrm{f}\left(\mathrm{t}\right)=\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{\mathrm{e}^{−\mathrm{tx}} }{\mathrm{x}}\mathrm{dt}=\frac{\mathrm{1}}{\mathrm{s}}\mathrm{ln}\left(\mathrm{s}+\mathrm{1}\right) \\ $$
Commented by mnjuly1970 last updated on 06/Mar/25

$$\:\cancel{\underline{ }} \\ $$
