
Question Number 86375 by mathmax by abdo last updated on 28/Mar/20
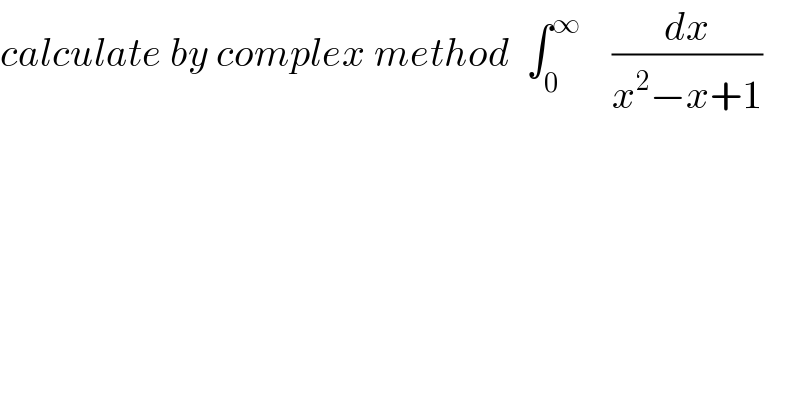
$${calculate}\:{by}\:{complex}\:{method}\:\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{dx}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}} \\ $$
Commented by mathmax by abdo last updated on 30/Mar/20
![first let find the value of this integral we have ∫ (dx/(x^2 −x +1)) =∫ (dx/((x−(1/2))^2 +(3/4))) =_(x−(1/2)=((√3)/2)u) (4/3)∫ (1/(u^2 +1))×((√3)/2)du =(2/(√3)) arctan(u) +c =(2/(√3))arctan(((2x−1)/(√3)))+C ⇒ ∫_0 ^∞ (dx/(x^2 −x+1)) =[(2/(√3))arctan(((2x−1)/(√3)))]_0 ^(+∞) =(2/(√3)){ (π/2) +arctan((1/(√3)))} =(2/(√3)){(π/2) +(π/6)} =(2/(√3)){((4π)/6)} =(2/(√3))×((2π)/3) =((4π)/(3(√3))) now let use complex method the problem come from 0 ! x^2 −x+1 =0 →Δ =−3 ⇒x_1 =((1+i(√3))/2)=e^((iπ)/3) and x_2 =((1−i(√3))/2) =e^(−((iπ)/3)) ⇒∫ (dx/(x^2 −x+1)) =∫ (dx/((x−e^((iπ)/3) )(x−e^(−((iπ)/3)) )))=(1/(2isin((π/3))))∫ ((1/(x−e^((iπ)/3) ))−(1/(x−e^(−((iπ)/3)) )))dx =(1/(i(√3)))ln(((x−e^((iπ)/3) )/(x−e^(−((iπ)/3)) ))) +C ⇒ ∫_0 ^∞ (dx/(x^2 −x+1)) =(1/(i(√3)))[ln(((x−e^((iπ)/3) )/(x−e^(−((iπ)/3)) )))]_0 ^(+∞) =(1/(i(√3))){−ln( e^((2iπ)/3) )} =−(1/(i(√3)))(((2iπ)/3)) =((2π)/(3(√3))) not correct the problem comes from0 let change 0 by 1 ∫_1 ^(+∞) (dx/(x^2 −x+1)) =(2/(√3))[arctan(((2x−1)/(√3)))]_1 ^(+∞) =(2/(√3)){ (π/2) −arctan((1/(√3)))} =(2/(√3)){(π/2)−(π/6)} =(2/(√3)){(π/3)} =((2π)/(3(√3))) complex method→∫_1 ^(+∞) (dx/(x^2 −x+1)) =(1/(i(√3)))[ln(((x−e^((iπ)/3) )/(x−e^(−((iπ)/3)) )))]_1 ^(+∞) =(1/(i(√3)))(−ln(((1−e^((iπ)/3) )/(1−e^(−((iπ)/3)) )))) we have ((1−e^((iπ)/3) )/(1−e^(−((iπ)/3)) )) =((1−(1/2)−i((√3)/2))/(1−(1/2)+i((√3)/2))) =(((1/2)−i((√3)/2))/((1/2)+((i(√3))/2))) =(e^(−((iπ)/3)) /e^((iπ)/3) ) =e^(−((2iπ)/3)) ⇒ ln(...) =−((2iπ)/3) ⇒∫_1 ^(+∞) (dx/(x^2 −x+1)) =(1/(i(√3)))(((−2iπ)/3)) =((−2π)/(3(√3))) (probleme of −) i have 2 remark here dont use complex method if you have 0 in the integral the function x→(1/(x^2 −x+1)) is ≥0 ⇒∫_1 ^(+∞) (dx/(x^2 −x)) ≥0 so you must eradicate − in the value....](Q86754.png)
$${first}\:{let}\:{find}\:{the}\:{value}\:{of}\:{this}\:{integral} \\ $$$${we}\:{have}\:\int\:\:\frac{{dx}}{{x}^{\mathrm{2}} −{x}\:+\mathrm{1}}\:=\int\:\:\frac{{dx}}{\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\frac{\mathrm{3}}{\mathrm{4}}}\:=_{{x}−\frac{\mathrm{1}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{u}} \:\:\frac{\mathrm{4}}{\mathrm{3}}\int\:\:\frac{\mathrm{1}}{{u}^{\mathrm{2}} \:+\mathrm{1}}×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{du} \\ $$$$=\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}\:{arctan}\left({u}\right)\:+{c}\:=\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}{arctan}\left(\frac{\mathrm{2}{x}−\mathrm{1}}{\sqrt{\mathrm{3}}}\right)+{C}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dx}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}\:=\left[\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}{arctan}\left(\frac{\mathrm{2}{x}−\mathrm{1}}{\sqrt{\mathrm{3}}}\right)\right]_{\mathrm{0}} ^{+\infty} \:=\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}\left\{\:\frac{\pi}{\mathrm{2}}\:+{arctan}\left(\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\right)\right\} \\ $$$$=\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}\left\{\frac{\pi}{\mathrm{2}}\:+\frac{\pi}{\mathrm{6}}\right\}\:=\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}\left\{\frac{\mathrm{4}\pi}{\mathrm{6}}\right\}\:=\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}×\frac{\mathrm{2}\pi}{\mathrm{3}}\:=\frac{\mathrm{4}\pi}{\mathrm{3}\sqrt{\mathrm{3}}} \\ $$$${now}\:\:{let}\:{use}\:{complex}\:{method}\:\:{the}\:{problem}\:{come}\:{from}\:\mathrm{0}\:! \\ $$$${x}^{\mathrm{2}} −{x}+\mathrm{1}\:=\mathrm{0}\:\rightarrow\Delta\:=−\mathrm{3}\:\Rightarrow{x}_{\mathrm{1}} =\frac{\mathrm{1}+{i}\sqrt{\mathrm{3}}}{\mathrm{2}}={e}^{\frac{{i}\pi}{\mathrm{3}}} \:{and}\:{x}_{\mathrm{2}} =\frac{\mathrm{1}−{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\:={e}^{−\frac{{i}\pi}{\mathrm{3}}} \\ $$$$\Rightarrow\int\:\:\frac{{dx}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}\:=\int\:\:\frac{{dx}}{\left({x}−{e}^{\frac{{i}\pi}{\mathrm{3}}} \right)\left({x}−{e}^{−\frac{{i}\pi}{\mathrm{3}}} \right)}=\frac{\mathrm{1}}{\mathrm{2}{isin}\left(\frac{\pi}{\mathrm{3}}\right)}\int\:\left(\frac{\mathrm{1}}{{x}−{e}^{\frac{{i}\pi}{\mathrm{3}}} }−\frac{\mathrm{1}}{{x}−{e}^{−\frac{{i}\pi}{\mathrm{3}}} }\right){dx} \\ $$$$=\frac{\mathrm{1}}{{i}\sqrt{\mathrm{3}}}{ln}\left(\frac{{x}−{e}^{\frac{{i}\pi}{\mathrm{3}}} }{{x}−{e}^{−\frac{{i}\pi}{\mathrm{3}}} }\right)\:+{C}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dx}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}\:=\frac{\mathrm{1}}{{i}\sqrt{\mathrm{3}}}\left[{ln}\left(\frac{{x}−{e}^{\frac{{i}\pi}{\mathrm{3}}} }{{x}−{e}^{−\frac{{i}\pi}{\mathrm{3}}} }\right)\right]_{\mathrm{0}} ^{+\infty} \:=\frac{\mathrm{1}}{{i}\sqrt{\mathrm{3}}}\left\{−{ln}\left(\:{e}^{\frac{\mathrm{2}{i}\pi}{\mathrm{3}}} \right)\right\} \\ $$$$=−\frac{\mathrm{1}}{{i}\sqrt{\mathrm{3}}}\left(\frac{\mathrm{2}{i}\pi}{\mathrm{3}}\right)\:=\frac{\mathrm{2}\pi}{\mathrm{3}\sqrt{\mathrm{3}}}\:\:{not}\:{correct}\:{the}\:{problem}\:{comes}\:{from}\mathrm{0} \\ $$$${let}\:{change}\:\mathrm{0}\:{by}\:\mathrm{1} \\ $$$$\int_{\mathrm{1}} ^{+\infty} \:\:\frac{{dx}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}\:=\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}\left[{arctan}\left(\frac{\mathrm{2}{x}−\mathrm{1}}{\sqrt{\mathrm{3}}}\right)\right]_{\mathrm{1}} ^{+\infty} \\ $$$$=\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}\left\{\:\frac{\pi}{\mathrm{2}}\:−{arctan}\left(\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\right)\right\}\:=\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}\left\{\frac{\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{6}}\right\}\:=\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}\left\{\frac{\pi}{\mathrm{3}}\right\}\:=\frac{\mathrm{2}\pi}{\mathrm{3}\sqrt{\mathrm{3}}} \\ $$$${complex}\:{method}\rightarrow\int_{\mathrm{1}} ^{+\infty} \:\frac{{dx}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}\:=\frac{\mathrm{1}}{{i}\sqrt{\mathrm{3}}}\left[{ln}\left(\frac{{x}−{e}^{\frac{{i}\pi}{\mathrm{3}}} }{{x}−{e}^{−\frac{{i}\pi}{\mathrm{3}}} }\right)\right]_{\mathrm{1}} ^{+\infty} \\ $$$$=\frac{\mathrm{1}}{{i}\sqrt{\mathrm{3}}}\left(−{ln}\left(\frac{\mathrm{1}−{e}^{\frac{{i}\pi}{\mathrm{3}}} }{\mathrm{1}−{e}^{−\frac{{i}\pi}{\mathrm{3}}} }\right)\right)\:\:{we}\:{have} \\ $$$$\frac{\mathrm{1}−{e}^{\frac{{i}\pi}{\mathrm{3}}} }{\mathrm{1}−{e}^{−\frac{{i}\pi}{\mathrm{3}}} }\:=\frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}−{i}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}+{i}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}\:=\frac{\frac{\mathrm{1}}{\mathrm{2}}−{i}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}{\frac{\mathrm{1}}{\mathrm{2}}+\frac{{i}\sqrt{\mathrm{3}}}{\mathrm{2}}}\:=\frac{{e}^{−\frac{{i}\pi}{\mathrm{3}}} }{{e}^{\frac{{i}\pi}{\mathrm{3}}} }\:={e}^{−\frac{\mathrm{2}{i}\pi}{\mathrm{3}}} \:\Rightarrow \\ $$$${ln}\left(...\right)\:=−\frac{\mathrm{2}{i}\pi}{\mathrm{3}}\:\Rightarrow\int_{\mathrm{1}} ^{+\infty} \:\frac{{dx}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}\:=\frac{\mathrm{1}}{{i}\sqrt{\mathrm{3}}}\left(\frac{−\mathrm{2}{i}\pi}{\mathrm{3}}\right)\:=\frac{−\mathrm{2}\pi}{\mathrm{3}\sqrt{\mathrm{3}}}\:\:\left({probleme}\:{of}\:−\right) \\ $$$${i}\:{have}\:\mathrm{2}\:{remark}\:{here}\:\: \\ $$$${dont}\:{use}\:{complex}\:{method}\:{if}\:{you}\:{have}\:\mathrm{0}\:{in}\:{the}\:{integral} \\ $$$${the}\:{function}\:{x}\rightarrow\frac{\mathrm{1}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}\:{is}\:\geqslant\mathrm{0}\:\Rightarrow\int_{\mathrm{1}} ^{+\infty} \:\frac{{dx}}{{x}^{\mathrm{2}} −{x}}\:\geqslant\mathrm{0}\:{so} \\ $$$${you}\:{must}\:{eradicate}\:−\:{in}\:{the}\:{value}.... \\ $$$$ \\ $$
Commented by redmiiuser last updated on 31/Mar/20
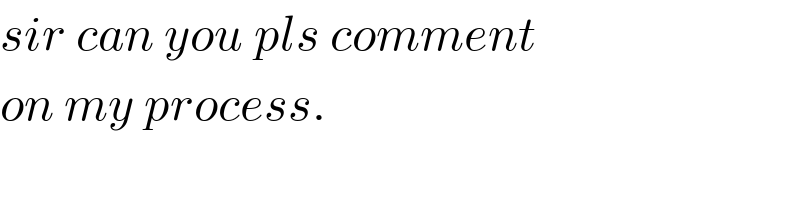
$${sir}\:{can}\:{you}\:{pls}\:{comment} \\ $$$${on}\:{my}\:{process}. \\ $$
Answered by redmiiuser last updated on 30/Mar/20
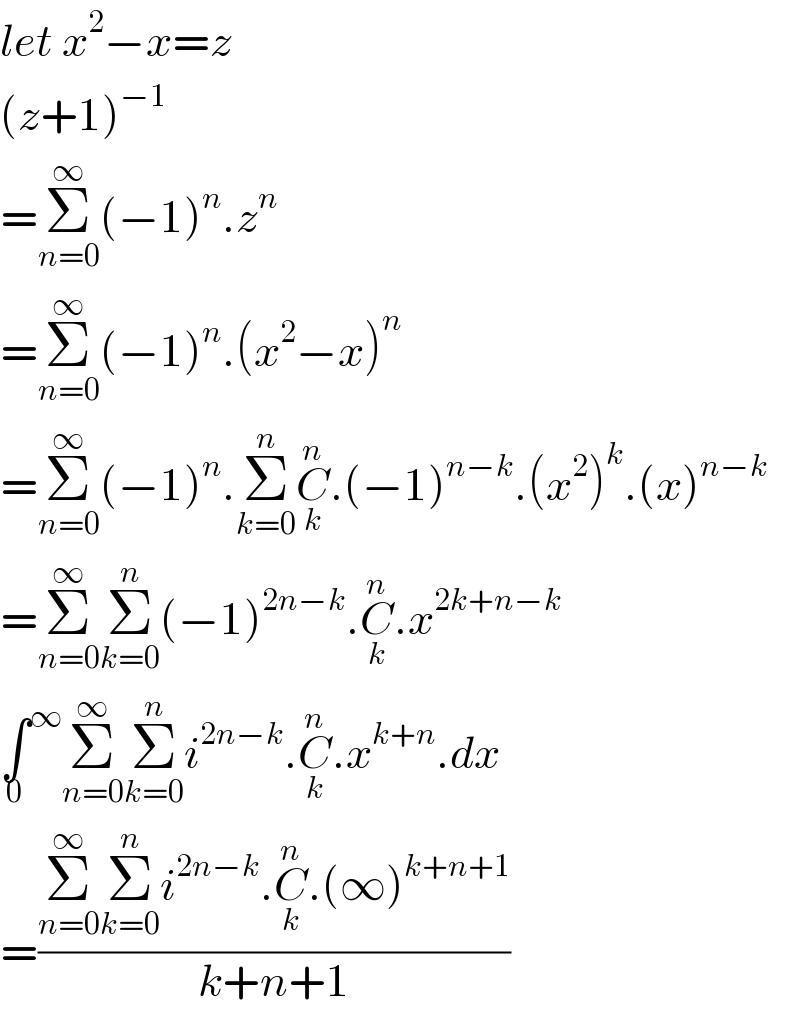
$${let}\:{x}^{\mathrm{2}} −{x}={z} \\ $$$$\left({z}+\mathrm{1}\right)^{−\mathrm{1}} \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} .{z}^{{n}} \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} .\left({x}^{\mathrm{2}} −{x}\right)^{{n}} \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} .\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\underset{{k}} {\overset{{n}} {{C}}}.\left(−\mathrm{1}\right)^{{n}−{k}} .\left({x}^{\mathrm{2}} \right)^{{k}} .\left({x}\right)^{{n}−{k}} \:\:\: \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\left(−\mathrm{1}\right)^{\mathrm{2}{n}−{k}} .\underset{{k}} {\overset{{n}} {{C}}}.{x}^{\mathrm{2}{k}+{n}−{k}} \\ $$$$\underset{\mathrm{0}} {\int}^{\infty} \underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{i}^{\mathrm{2}{n}−{k}} .\underset{{k}} {\overset{{n}} {{C}}}.{x}^{{k}+{n}} .{dx} \\ $$$$=\frac{\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{i}^{\mathrm{2}{n}−{k}} .\underset{{k}} {\overset{{n}} {{C}}}.\left(\infty\right)^{{k}+{n}+\mathrm{1}} }{{k}+{n}+\mathrm{1}} \\ $$
Commented by redmiiuser last updated on 30/Mar/20

$${sir}\:{can}\:{you}\:{pls}\:{check} \\ $$$${the}\:{answer}. \\ $$
Commented by mathmax by abdo last updated on 01/Apr/20
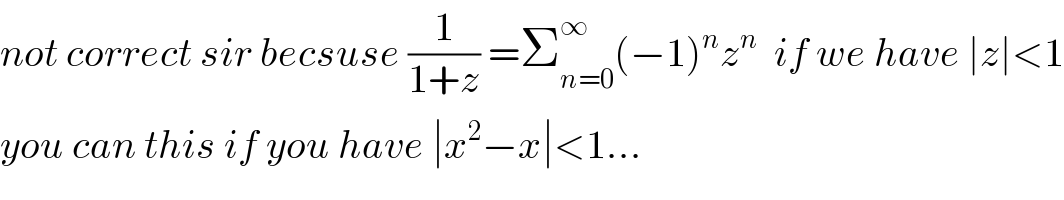
$${not}\:{correct}\:{sir}\:{becsuse}\:\frac{\mathrm{1}}{\mathrm{1}+{z}}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} {z}^{{n}} \:\:{if}\:{we}\:{have}\:\mid{z}\mid<\mathrm{1} \\ $$$${you}\:{can}\:{this}\:{if}\:{you}\:{have}\:\mid{x}^{\mathrm{2}} −{x}\mid<\mathrm{1}... \\ $$
Commented by redmiiuser last updated on 01/Apr/20

$${sir}\:{can}\:{you}\:{pls}\:{check}\: \\ $$$$\frac{\mathrm{1}}{{z}+\mathrm{1}}\:{expansion}\:{by} \\ $$$${Taloyr}'{s}\:\:{formula}. \\ $$
Commented by redmiiuser last updated on 03/Apr/20
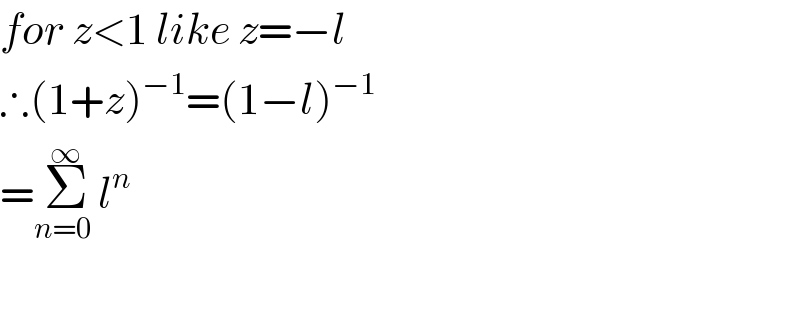
$${for}\:{z}<\mathrm{1}\:{like}\:{z}=−{l} \\ $$$$\therefore\left(\mathrm{1}+{z}\right)^{−\mathrm{1}} =\left(\mathrm{1}−{l}\right)^{−\mathrm{1}} \\ $$$$=\underset{{n}=\mathrm{0}\:} {\overset{\infty} {\sum}}{l}^{{n}} \\ $$$$ \\ $$
