
Question Number 207352 by NasaSara last updated on 12/May/24
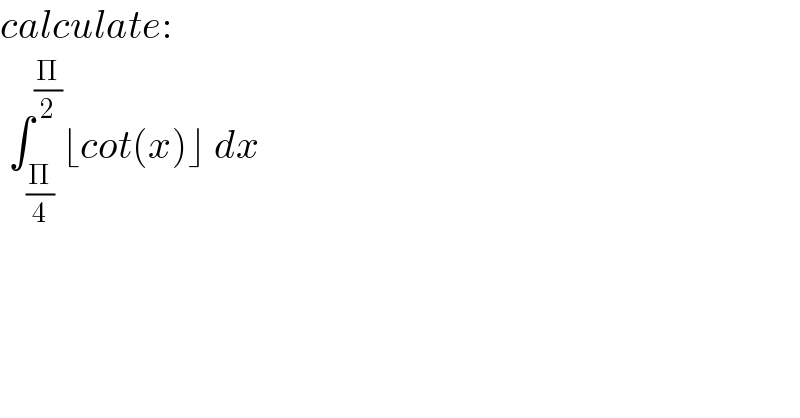
$${calculate}: \\ $$$$\:\int_{\frac{\Pi}{\mathrm{4}}} ^{\frac{\Pi}{\mathrm{2}}} \lfloor{cot}\left({x}\right)\rfloor\:{dx} \\ $$
Commented by NasaSara last updated on 12/May/24

$${thank}\:{you} \\ $$
Commented by Berbere last updated on 12/May/24

$${withe}\:{Pleasur} \\ $$
Commented by Berbere last updated on 12/May/24
;(π/2)]⇒[cot(x)]=0 ∫_(π/4) ^(π/2) [cot(x)]dx=0](Q207355.png)
$$\left.\mathrm{0}\left.\leqslant{cot}\left({x}\right)<\mathrm{1}\:;\forall{x}\in\right]\frac{\pi}{\mathrm{4}};\frac{\pi}{\mathrm{2}}\right]\Rightarrow\left[{cot}\left({x}\right)\right]=\mathrm{0} \\ $$$$\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{2}}} \left[{cot}\left({x}\right)\right]{dx}=\mathrm{0} \\ $$
Answered by MM42 last updated on 12/May/24
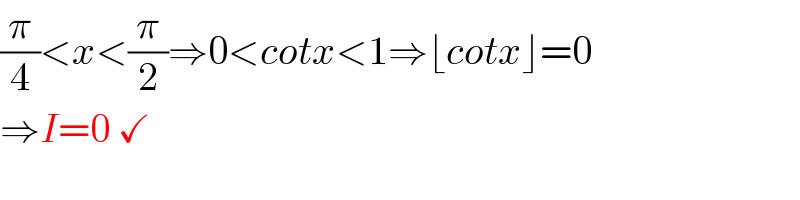
$$\frac{\pi}{\mathrm{4}}<{x}<\frac{\pi}{\mathrm{2}}\Rightarrow\mathrm{0}<{cotx}<\mathrm{1}\Rightarrow\lfloor{cotx}\rfloor=\mathrm{0} \\ $$$$\Rightarrow{I}=\mathrm{0}\:\checkmark \\ $$
