
Question Number 35427 by abdo.msup.com last updated on 18/May/18
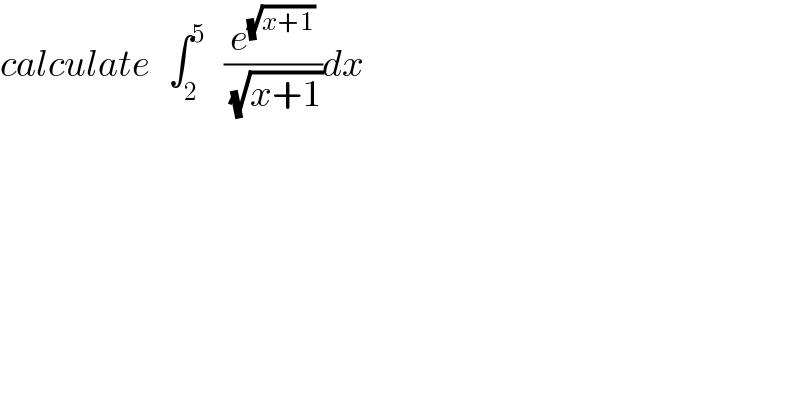
$${calculate}\:\:\:\int_{\mathrm{2}} ^{\mathrm{5}} \:\:\:\frac{{e}^{\sqrt{{x}+\mathrm{1}}} }{\sqrt{{x}+\mathrm{1}}}{dx} \\ $$
Commented by prof Abdo imad last updated on 19/May/18
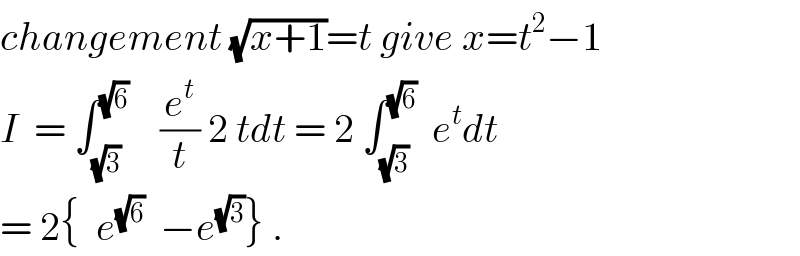
$${changement}\:\sqrt{{x}+\mathrm{1}}={t}\:{give}\:{x}={t}^{\mathrm{2}} −\mathrm{1} \\ $$$${I}\:\:=\:\int_{\sqrt{\mathrm{3}}} ^{\sqrt{\mathrm{6}}} \:\:\:\:\frac{{e}^{{t}} }{{t}}\:\mathrm{2}\:{tdt}\:=\:\mathrm{2}\:\int_{\sqrt{\mathrm{3}}} ^{\sqrt{\mathrm{6}}} \:\:{e}^{{t}} {dt} \\ $$$$=\:\mathrm{2}\left\{\:\:{e}^{\sqrt{\mathrm{6}}} \:\:−{e}^{\sqrt{\mathrm{3}}} \right\}\:. \\ $$
Answered by ajfour last updated on 19/May/18
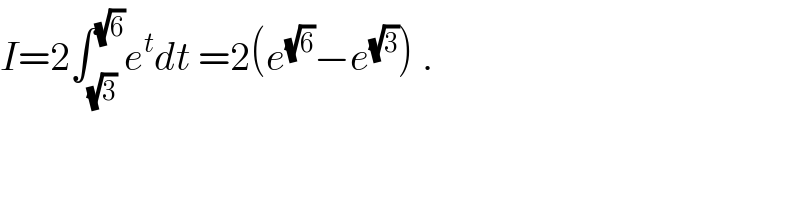
$${I}=\mathrm{2}\int_{\sqrt{\mathrm{3}}} ^{\sqrt{\mathrm{6}}} {e}^{{t}} {dt}\:=\mathrm{2}\left({e}^{\sqrt{\mathrm{6}}} −{e}^{\sqrt{\mathrm{3}}} \right)\:. \\ $$
