
Question Number 67530 by mathmax by abdo last updated on 28/Aug/19
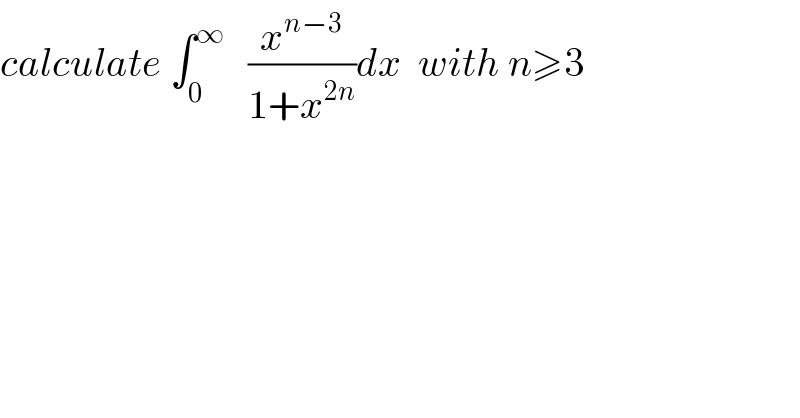
$${calculate}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{x}^{{n}−\mathrm{3}} }{\mathrm{1}+{x}^{\mathrm{2}{n}} }{dx}\:\:{with}\:{n}\geqslant\mathrm{3} \\ $$
Commented by ~ À ® @ 237 ~ last updated on 29/Aug/19
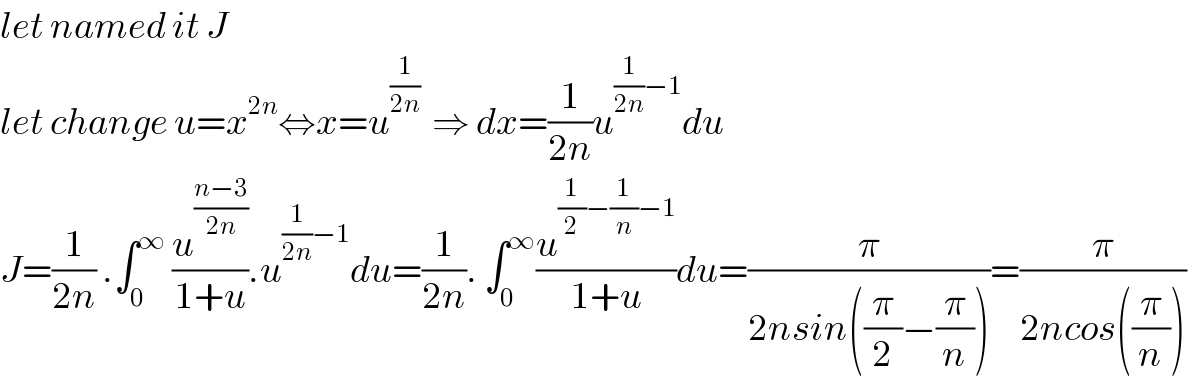
$${let}\:{named}\:{it}\:{J} \\ $$$${let}\:{change}\:{u}={x}^{\mathrm{2}{n}} \Leftrightarrow{x}={u}^{\frac{\mathrm{1}}{\mathrm{2}{n}}} \:\:\Rightarrow\:{dx}=\frac{\mathrm{1}}{\mathrm{2}{n}}{u}^{\frac{\mathrm{1}}{\mathrm{2}{n}}−\mathrm{1}} {du} \\ $$$${J}=\frac{\mathrm{1}}{\mathrm{2}{n}}\:.\int_{\mathrm{0}} ^{\infty} \:\frac{{u}^{\frac{{n}−\mathrm{3}}{\mathrm{2}{n}}} }{\mathrm{1}+{u}}.{u}^{\frac{\mathrm{1}}{\mathrm{2}{n}}−\mathrm{1}} {du}=\frac{\mathrm{1}}{\mathrm{2}{n}}.\:\int_{\mathrm{0}} ^{\infty} \frac{{u}^{\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{{n}}−\mathrm{1}} }{\mathrm{1}+{u}}{du}=\frac{\pi}{\mathrm{2}{nsin}\left(\frac{\pi}{\mathrm{2}}−\frac{\pi}{{n}}\right)}=\frac{\pi}{\mathrm{2}{ncos}\left(\frac{\pi}{{n}}\right)}\: \\ $$
Commented by Abdo msup. last updated on 29/Aug/19

$${thanks}\:{sir}. \\ $$
