
Question Number 197024 by mnjuly1970 last updated on 06/Sep/23
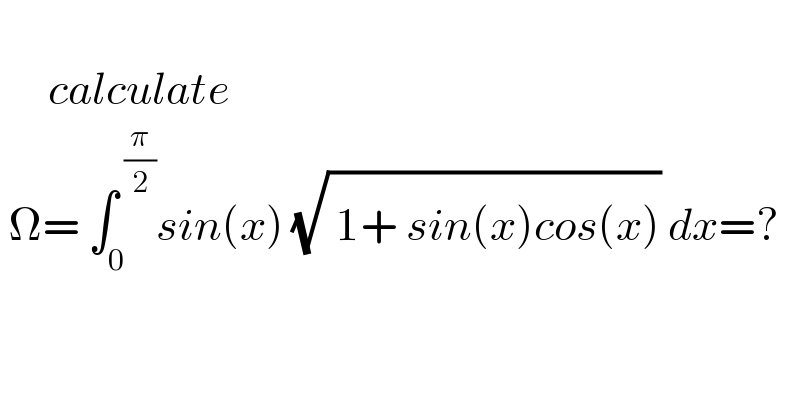
$$ \\ $$$$\:\:\:\:\:\:{calculate} \\ $$$$\:\Omega=\:\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} {sin}\left({x}\right)\:\sqrt{\:\mathrm{1}\overset{} {+}\:{sin}\left({x}\right){cos}\left({x}\right)}\:{dx}=? \\ $$$$ \\ $$
Answered by Frix last updated on 06/Sep/23
![∫sin x (√(1+sin x cos x)) dx =^(t=x−(π/4)) =∫(((cos t +sin t)(√(1+2cos^2 t)))/2)dt =^(u=tan t) =∫(((u+1)(√(u^2 +3)))/(2(u^2 +1)^2 ))du =^(v=((u+(√(u^2 +3)))/( (√3)))) =∫(((√3)((√3)v−1)((√3)v+3)(v^2 +1)^2 )/((3v^4 −2v^2 +3)^2 ))dv =_(Method) ^(Ostrogradski′s) =−(((√3)v^3 −v^2 +(√3)v+3)/(2(3v^4 −2v^2 +3)))+∫(((√3)v^2 +6v−(√3))/(2(3v^4 −2v^2 +3)))dv= =−(((√3)v^3 −v^2 +(√3)v+3)/(2(3v^4 −2v^2 +3)))+((√2)/(16))ln ((3v^2 −2(√6)v+3)/(3v^2 +2(√6)v+3))+((3(√2))/8)(tan^(−1) ((√3)v−(√2)) −tan^(−1) ((√3)v+(√2))) x∈[0, (π/2)] ⇒ v∈[((√3)/3), (√3)] ⇒ Ω=((3(√2)π)/(16))+(1/2)−((3(√2))/8)tan^(−1) ((√2)/4) ≈1.15281482](Q197026.png)
$$\int\mathrm{sin}\:{x}\:\sqrt{\mathrm{1}+\mathrm{sin}\:{x}\:\mathrm{cos}\:{x}}\:{dx}\:\overset{{t}={x}−\frac{\pi}{\mathrm{4}}} {=} \\ $$$$=\int\frac{\left(\mathrm{cos}\:{t}\:+\mathrm{sin}\:{t}\right)\sqrt{\mathrm{1}+\mathrm{2cos}^{\mathrm{2}} \:{t}}}{\mathrm{2}}{dt}\:\overset{{u}=\mathrm{tan}\:\:{t}} {=} \\ $$$$=\int\frac{\left({u}+\mathrm{1}\right)\sqrt{{u}^{\mathrm{2}} +\mathrm{3}}}{\mathrm{2}\left({u}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{du}\:\overset{{v}=\frac{{u}+\sqrt{{u}^{\mathrm{2}} +\mathrm{3}}}{\:\sqrt{\mathrm{3}}}} {=} \\ $$$$=\int\frac{\sqrt{\mathrm{3}}\left(\sqrt{\mathrm{3}}{v}−\mathrm{1}\right)\left(\sqrt{\mathrm{3}}{v}+\mathrm{3}\right)\left({v}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{\left(\mathrm{3}{v}^{\mathrm{4}} −\mathrm{2}{v}^{\mathrm{2}} +\mathrm{3}\right)^{\mathrm{2}} }{dv}\:\underset{\mathrm{Method}} {\overset{\mathrm{Ostrogradski}'\mathrm{s}} {=}} \\ $$$$=−\frac{\sqrt{\mathrm{3}}{v}^{\mathrm{3}} −{v}^{\mathrm{2}} +\sqrt{\mathrm{3}}{v}+\mathrm{3}}{\mathrm{2}\left(\mathrm{3}{v}^{\mathrm{4}} −\mathrm{2}{v}^{\mathrm{2}} +\mathrm{3}\right)}+\int\frac{\sqrt{\mathrm{3}}{v}^{\mathrm{2}} +\mathrm{6}{v}−\sqrt{\mathrm{3}}}{\mathrm{2}\left(\mathrm{3}{v}^{\mathrm{4}} −\mathrm{2}{v}^{\mathrm{2}} +\mathrm{3}\right)}{dv}= \\ $$$$=−\frac{\sqrt{\mathrm{3}}{v}^{\mathrm{3}} −{v}^{\mathrm{2}} +\sqrt{\mathrm{3}}{v}+\mathrm{3}}{\mathrm{2}\left(\mathrm{3}{v}^{\mathrm{4}} −\mathrm{2}{v}^{\mathrm{2}} +\mathrm{3}\right)}+\frac{\sqrt{\mathrm{2}}}{\mathrm{16}}\mathrm{ln}\:\frac{\mathrm{3}{v}^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{6}}{v}+\mathrm{3}}{\mathrm{3}{v}^{\mathrm{2}} +\mathrm{2}\sqrt{\mathrm{6}}{v}+\mathrm{3}}+\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{8}}\left(\mathrm{tan}^{−\mathrm{1}} \:\left(\sqrt{\mathrm{3}}{v}−\sqrt{\mathrm{2}}\right)\:−\mathrm{tan}^{−\mathrm{1}} \:\left(\sqrt{\mathrm{3}}{v}+\sqrt{\mathrm{2}}\right)\right) \\ $$$${x}\in\left[\mathrm{0},\:\frac{\pi}{\mathrm{2}}\right]\:\Rightarrow\:{v}\in\left[\frac{\sqrt{\mathrm{3}}}{\mathrm{3}},\:\sqrt{\mathrm{3}}\right] \\ $$$$\Rightarrow \\ $$$$\Omega=\frac{\mathrm{3}\sqrt{\mathrm{2}}\pi}{\mathrm{16}}+\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{8}}\mathrm{tan}^{−\mathrm{1}} \:\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\:\approx\mathrm{1}.\mathrm{15281482} \\ $$
Commented by mnjuly1970 last updated on 06/Sep/23
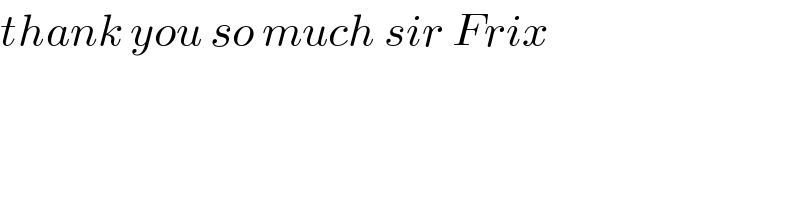
$${thank}\:{you}\:{so}\:{much}\:{sir}\:{Frix} \\ $$$$ \\ $$
Commented by Frix last updated on 06/Sep/23
��
Answered by universe last updated on 10/Sep/23
![2I = ∫_0 ^(π/2) (sin x+cos x)(√((3/2)−(1/2)(sin x−cos x)^2 ))dx let sin x−cos x = t ⇒ (sin x+cos x)dx = dt I = (1/(2(√2)))∫_(−1) ^1 (√(3 − t^2 )) dt I = (1/( (√2)))∫_0 ^1 (√(((√3))^2 −t^2 ))dt I = (1/( (√2)))[(t/2)(√(3−t^2 )) + (3/2)sin^(−1) (t/( (√3)))]_0 ^1 I = (1/(2(√2)))[(√2) + 3sin^(−1) (1/( (√3)))]](Q197039.png)
$$ \\ $$$$\mathrm{2}{I}\:\:=\:\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \left(\mathrm{sin}\:{x}+\mathrm{cos}\:{x}\right)\sqrt{\frac{\mathrm{3}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{sin}\:{x}−\mathrm{cos}\:{x}\right)^{\mathrm{2}} }{dx} \\ $$$${let} \\ $$$$\mathrm{sin}\:{x}−\mathrm{cos}\:{x}\:=\:{t}\:\Rightarrow\:\left(\mathrm{sin}\:{x}+\mathrm{cos}\:{x}\right){dx}\:=\:{dt} \\ $$$${I}\:=\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\int_{−\mathrm{1}} ^{\mathrm{1}} \sqrt{\mathrm{3}\:−\:{t}^{\mathrm{2}} }\:\:{dt} \\ $$$${I}\:\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\left(\sqrt{\mathrm{3}}\right)^{\mathrm{2}} −{t}^{\mathrm{2}} }{dt} \\ $$$${I}\:\:=\:\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left[\frac{{t}}{\mathrm{2}}\sqrt{\mathrm{3}−{t}^{\mathrm{2}} \:}\:+\:\frac{\mathrm{3}}{\mathrm{2}}\mathrm{sin}^{−\mathrm{1}} \frac{{t}}{\:\sqrt{\mathrm{3}}}\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$${I}\:\:=\:\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\left[\sqrt{\mathrm{2}}\:+\:\mathrm{3sin}^{−\mathrm{1}} \frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right] \\ $$
Commented by mnjuly1970 last updated on 06/Sep/23
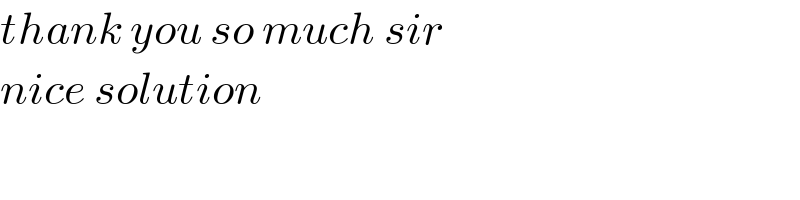
$${thank}\:{you}\:{so}\:{much}\:{sir} \\ $$$${nice}\:{solution} \\ $$
Answered by ajfour last updated on 07/Sep/23
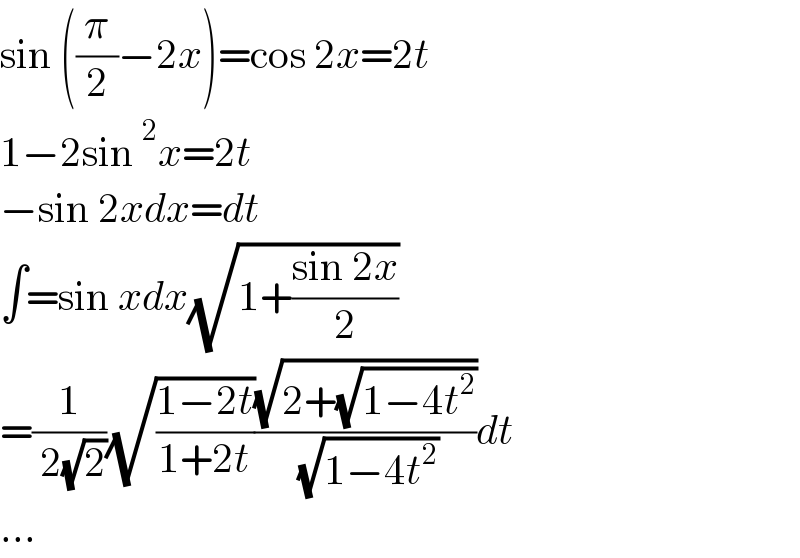
$$\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}−\mathrm{2}{x}\right)=\mathrm{cos}\:\mathrm{2}{x}=\mathrm{2}{t} \\ $$$$\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} {x}=\mathrm{2}{t} \\ $$$$−\mathrm{sin}\:\mathrm{2}{xdx}={dt} \\ $$$$\int=\mathrm{sin}\:{xdx}\sqrt{\mathrm{1}+\frac{\mathrm{sin}\:\mathrm{2}{x}}{\mathrm{2}}} \\ $$$$=\frac{\mathrm{1}}{\:\mathrm{2}\sqrt{\mathrm{2}}}\sqrt{\frac{\mathrm{1}−\mathrm{2}{t}}{\mathrm{1}+\mathrm{2}{t}}}\frac{\sqrt{\mathrm{2}+\sqrt{\mathrm{1}−\mathrm{4}{t}^{\mathrm{2}} }}}{\:\sqrt{\mathrm{1}−\mathrm{4}{t}^{\mathrm{2}} }}{dt} \\ $$$$... \\ $$
