
Question Number 200254 by mnjuly1970 last updated on 16/Nov/23
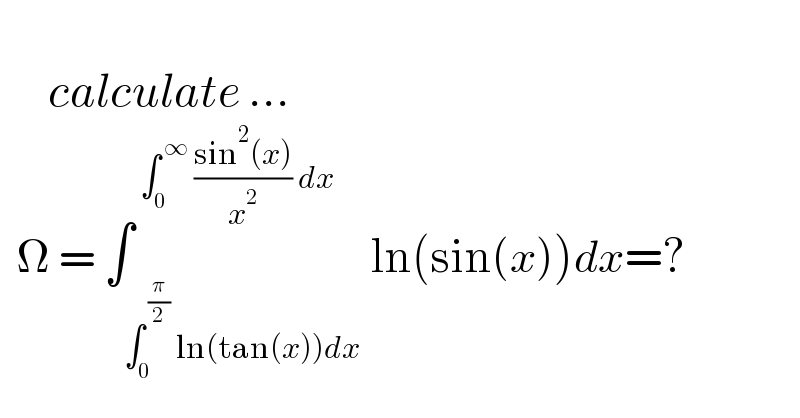
$$ \\ $$$$\:\:\:\:\:\:{calculate}\:... \\ $$$$\:\:\Omega\:=\:\int_{\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \:\mathrm{ln}\left(\mathrm{tan}\left({x}\right)\right){dx}} ^{\:\int_{\mathrm{0}} ^{\:\infty} \:\frac{\mathrm{sin}^{\mathrm{2}} \left({x}\right)}{{x}^{\mathrm{2}} }\:{dx}} \mathrm{ln}\left(\mathrm{sin}\left({x}\right)\right){dx}=? \\ $$
Answered by Mathspace last updated on 16/Nov/23
![its a triky integral we have ∫_0 ^(π/2) ln(tanx)dx =∫_0 ^(π/2) ln(((sinx)/(cosx)))dx =∫_0 ^(π/2) ln(sinx)dx−∫_0 ^(π/2) ln(cosx)dx=0(equal) ∫_0 ^∞ ((sin^2 x)/x^2 )dx=[−(1/x)sin^2 x]_0 ^∞ −∫_0 ^∞ (−(1/x))2sinx cosx dx =0+∫_0 ^∞ ((sin(2x))/x)dx (2x=t) =∫_0 ^∞ ((sint)/(t/2))(dt/2)=∫_0 ^∞ ((sint)/t)dt=(π/2) ⇒I=∫_0 ^(π/2) ln(sinx)dx =−(π/2)ln2](Q200287.png)
$${its}\:{a}\:{triky}\:{integral} \\ $$$${we}\:{have}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({tanx}\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left(\frac{{sinx}}{{cosx}}\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({sinx}\right){dx}−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({cosx}\right){dx}=\mathrm{0}\left({equal}\right) \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\frac{{sin}^{\mathrm{2}} {x}}{{x}^{\mathrm{2}} }{dx}=\left[−\frac{\mathrm{1}}{{x}}{sin}^{\mathrm{2}} {x}\right]_{\mathrm{0}} ^{\infty} \\ $$$$−\int_{\mathrm{0}} ^{\infty} \left(−\frac{\mathrm{1}}{{x}}\right)\mathrm{2}{sinx}\:{cosx}\:{dx} \\ $$$$=\mathrm{0}+\int_{\mathrm{0}} ^{\infty} \frac{{sin}\left(\mathrm{2}{x}\right)}{{x}}{dx}\:\:\:\left(\mathrm{2}{x}={t}\right) \\ $$$$=\int_{\mathrm{0}} ^{\infty} \frac{{sint}}{\frac{{t}}{\mathrm{2}}}\frac{{dt}}{\mathrm{2}}=\int_{\mathrm{0}} ^{\infty} \frac{{sint}}{{t}}{dt}=\frac{\pi}{\mathrm{2}} \\ $$$$\Rightarrow{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({sinx}\right){dx} \\ $$$$=−\frac{\pi}{\mathrm{2}}{ln}\mathrm{2} \\ $$
Commented by Calculusboy last updated on 16/Nov/23

$$\boldsymbol{{thanks}}\:\boldsymbol{{sir}} \\ $$
Commented by mnjuly1970 last updated on 17/Nov/23

$${thanks}\:{alot}\:{sir} \\ $$
