Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 47112 by maxmathsup by imad last updated on 04/Nov/18

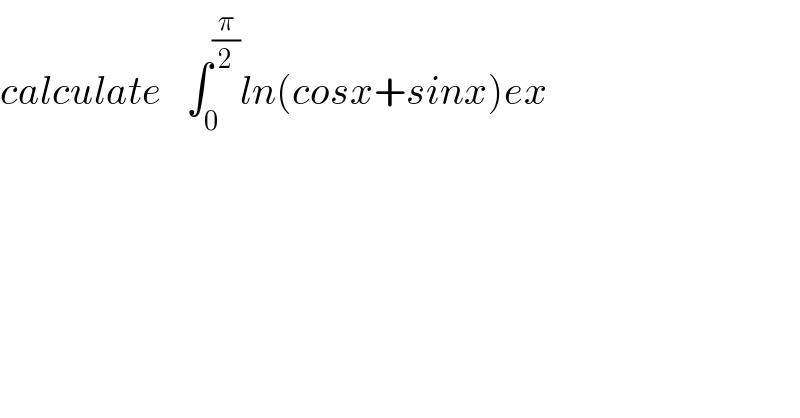
calculate ∫_0 ^(π/2) ln(cosx+sinx)ex

$${calculate}\:\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({cosx}+{sinx}\right){ex} \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 05/Nov/18

Commented by tanmay.chaudhury50@gmail.com last updated on 05/Nov/18

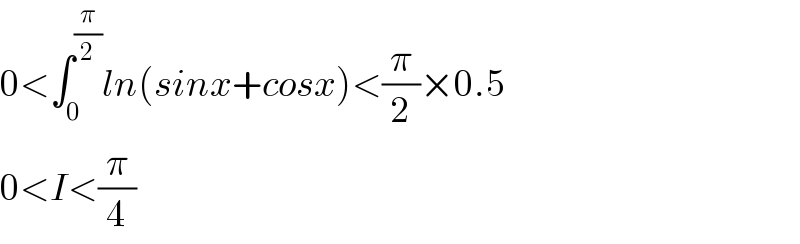
0<∫_0 ^(π/2) ln(sinx+cosx)<(π/2)×0.5 0<I<(π/4)

$$\mathrm{0}<\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({sinx}+{cosx}\right)<\frac{\pi}{\mathrm{2}}×\mathrm{0}.\mathrm{5} \\ $$$$\mathrm{0}<{I}<\frac{\pi}{\mathrm{4}} \\ $$

Commented by prof Abdo imad last updated on 06/Nov/18

let I =∫_0 ^(π/2) ln(cosx +sinx)dx ⇒ I =∫_0 ^(π/2) ln((√2)cos(x−(π/4)))dx=(π/4)ln(2)+∫_0 ^(π/2) ln(cos(x−(π/4)))dx but ∫_0 ^(π/2) ln(cos(x−(π/4)))dx=_((π/4)−x=t) −∫_(π/4) ^(−(π/4)) ln(cost)dt =∫_(−(π/4)) ^(π/4) ln(cost)dt =2 ∫_0 ^(π/4) ln(cost)dt let A =∫_0 ^(π/4) ln(cost)dt andB =∫_0 ^(π/4) ln(sint)dt A+B =∫_0 ^(π/4) ln(costsint)dt=∫_0 ^(π/4) ln(((sin(2t))/2))dt =−(π/4)ln(2)+∫_0 ^(π/4) ln(sin(2t))dt =_(2t=u) −(π/4)ln(2)+(1/2)∫_0 ^(π/2) ln(sinu)du =−(π/4)ln(2)−(π/4)ln(2)=−(π/2)ln(2) also A−B = ∫_0 ^(π/4) ln(cost)dt−∫_0 ^(π/4) ln(sint)dt but ∫_0 ^(π/4) ln(sint)dt =_(t=(π/2)−x) −∫_(π/2) ^(π/4) ln(cosx)dx =∫_(π/4) ^(π/2) ln(cosx)dx=∫_0 ^(π/2) ln(cosx)dx−∫_0 ^(π/4) ln(cosx)dx =−(π/2)ln(2)−A ⇒A−B =−(π/2)ln2−A ⇒ 2A =B−(π/2)ln(2) ⇒2A =−(π/2)ln(2)−A−(π/2)ln(2) ⇒2A =−A −πln(2) ⇒3A=−πln(2) ⇒ A=−(π/3)ln(2) ⇒I =−((2π)/3)ln(2).

$${let}\:{I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({cosx}\:+{sinx}\right){dx}\:\Rightarrow \\ $$$${I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left(\sqrt{\mathrm{2}}{cos}\left({x}−\frac{\pi}{\mathrm{4}}\right)\right){dx}=\frac{\pi}{\mathrm{4}}{ln}\left(\mathrm{2}\right)+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({cos}\left({x}−\frac{\pi}{\mathrm{4}}\right)\right){dx} \\ $$$${but}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({cos}\left({x}−\frac{\pi}{\mathrm{4}}\right)\right){dx}=_{\frac{\pi}{\mathrm{4}}−{x}={t}} −\int_{\frac{\pi}{\mathrm{4}}} ^{−\frac{\pi}{\mathrm{4}}} {ln}\left({cost}\right){dt} \\ $$$$=\int_{−\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{4}}} \:{ln}\left({cost}\right){dt}\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({cost}\right){dt} \\ $$$${let}\:{A}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({cost}\right){dt}\:{andB}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({sint}\right){dt} \\ $$$${A}+{B}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({costsint}\right){dt}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left(\frac{{sin}\left(\mathrm{2}{t}\right)}{\mathrm{2}}\right){dt} \\ $$$$=−\frac{\pi}{\mathrm{4}}{ln}\left(\mathrm{2}\right)+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({sin}\left(\mathrm{2}{t}\right)\right){dt} \\ $$$$=_{\mathrm{2}{t}={u}} \:−\frac{\pi}{\mathrm{4}}{ln}\left(\mathrm{2}\right)+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({sinu}\right){du} \\ $$$$=−\frac{\pi}{\mathrm{4}}{ln}\left(\mathrm{2}\right)−\frac{\pi}{\mathrm{4}}{ln}\left(\mathrm{2}\right)=−\frac{\pi}{\mathrm{2}}{ln}\left(\mathrm{2}\right)\:{also} \\ $$$${A}−{B}\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({cost}\right){dt}−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({sint}\right){dt}\:{but} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({sint}\right){dt}\:=_{{t}=\frac{\pi}{\mathrm{2}}−{x}} \:\:\:−\int_{\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({cosx}\right){dx} \\ $$$$=\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{2}}} \:{ln}\left({cosx}\right){dx}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({cosx}\right){dx}−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({cosx}\right){dx} \\ $$$$=−\frac{\pi}{\mathrm{2}}{ln}\left(\mathrm{2}\right)−{A}\:\Rightarrow{A}−{B}\:=−\frac{\pi}{\mathrm{2}}{ln}\mathrm{2}−{A}\:\Rightarrow \\ $$$$\mathrm{2}{A}\:={B}−\frac{\pi}{\mathrm{2}}{ln}\left(\mathrm{2}\right)\:\Rightarrow\mathrm{2}{A}\:=−\frac{\pi}{\mathrm{2}}{ln}\left(\mathrm{2}\right)−{A}−\frac{\pi}{\mathrm{2}}{ln}\left(\mathrm{2}\right) \\ $$$$\Rightarrow\mathrm{2}{A}\:=−{A}\:−\pi{ln}\left(\mathrm{2}\right)\:\Rightarrow\mathrm{3}{A}=−\pi{ln}\left(\mathrm{2}\right)\:\Rightarrow \\ $$$${A}=−\frac{\pi}{\mathrm{3}}{ln}\left(\mathrm{2}\right)\:\:\Rightarrow{I}\:=−\frac{\mathrm{2}\pi}{\mathrm{3}}{ln}\left(\mathrm{2}\right). \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 05/Nov/18

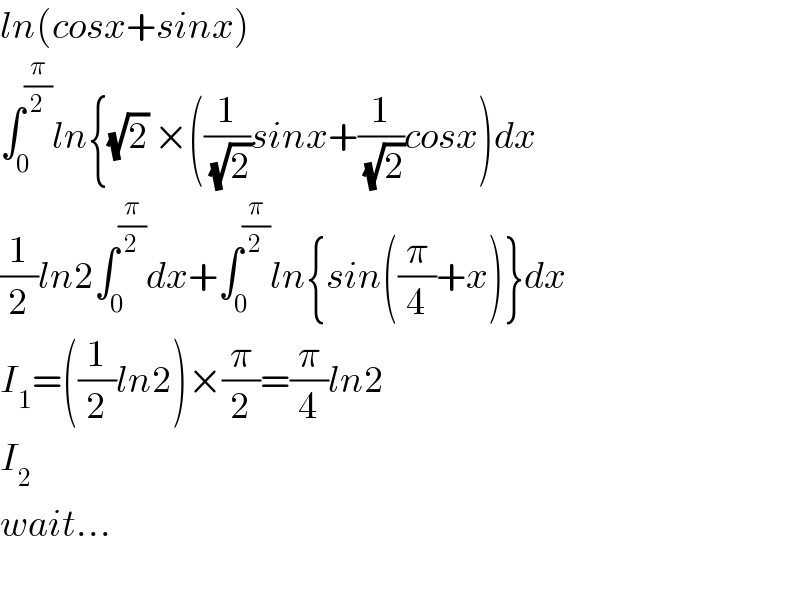
ln(cosx+sinx) ∫_0 ^(π/2) ln{(√2) ×((1/(√2))sinx+(1/(√2))cosx)dx (1/2)ln2∫_0 ^(π/2) dx+∫_0 ^(π/2) ln{sin((π/4)+x)}dx I_1 =((1/2)ln2)×(π/2)=(π/4)ln2 I_2 wait...

$${ln}\left({cosx}+{sinx}\right) \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left\{\sqrt{\mathrm{2}}\:×\left(\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}{sinx}+\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}{cosx}\right){dx}\right. \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{ln}\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {dx}+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left\{{sin}\left(\frac{\pi}{\mathrm{4}}+{x}\right)\right\}{dx} \\ $$$${I}_{\mathrm{1}} =\left(\frac{\mathrm{1}}{\mathrm{2}}{ln}\mathrm{2}\right)×\frac{\pi}{\mathrm{2}}=\frac{\pi}{\mathrm{4}}{ln}\mathrm{2} \\ $$$${I}_{\mathrm{2}} \: \\ $$$${wait}... \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com