Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 130135 by mathmax by abdo last updated on 22/Jan/21

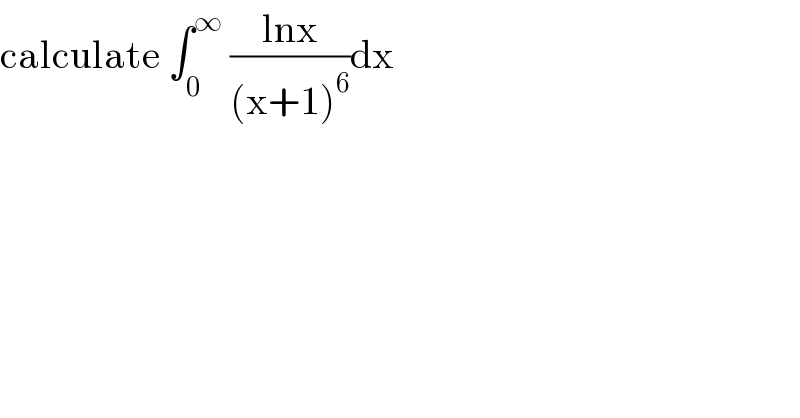
calculate ∫_0 ^∞ ((lnx)/((x+1)^6 ))dx

$$\mathrm{calculate}\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{lnx}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{6}} }\mathrm{dx} \\ $$

Answered by Dwaipayan Shikari last updated on 22/Jan/21

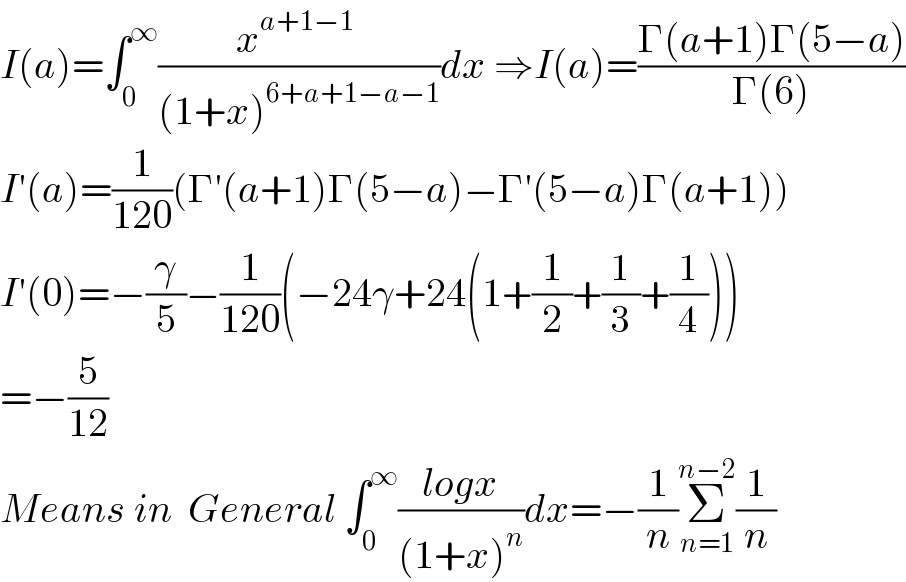
I(a)=∫_0 ^∞ ((x^(a+1−1) )/((1+x)^(6+a+1−a−1) ))dx ⇒I(a)=((Γ(a+1)Γ(5−a))/(Γ(6))) I′(a)=(1/(120))(Γ′(a+1)Γ(5−a)−Γ′(5−a)Γ(a+1)) I′(0)=−(γ/5)−(1/(120))(−24γ+24(1+(1/2)+(1/3)+(1/4))) =−(5/(12)) Means in General ∫_0 ^∞ ((logx)/((1+x)^n ))dx=−(1/n)Σ_(n=1) ^(n−2) (1/n)

$${I}\left({a}\right)=\int_{\mathrm{0}} ^{\infty} \frac{{x}^{{a}+\mathrm{1}−\mathrm{1}} \:}{\left(\mathrm{1}+{x}\right)^{\mathrm{6}+{a}+\mathrm{1}−{a}−\mathrm{1}} }{dx}\:\Rightarrow{I}\left({a}\right)=\frac{\Gamma\left({a}+\mathrm{1}\right)\Gamma\left(\mathrm{5}−{a}\right)}{\Gamma\left(\mathrm{6}\right)} \\ $$$${I}'\left({a}\right)=\frac{\mathrm{1}}{\mathrm{120}}\left(\Gamma'\left({a}+\mathrm{1}\right)\Gamma\left(\mathrm{5}−{a}\right)−\Gamma'\left(\mathrm{5}−{a}\right)\Gamma\left({a}+\mathrm{1}\right)\right) \\ $$$${I}'\left(\mathrm{0}\right)=−\frac{\gamma}{\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{120}}\left(−\mathrm{24}\gamma+\mathrm{24}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{4}}\right)\right) \\ $$$$=−\frac{\mathrm{5}}{\mathrm{12}} \\ $$$${Means}\:{in}\:\:{General}\:\int_{\mathrm{0}} ^{\infty} \frac{{logx}}{\left(\mathrm{1}+{x}\right)^{{n}} }{dx}=−\frac{\mathrm{1}}{{n}}\underset{{n}=\mathrm{1}} {\overset{{n}−\mathrm{2}} {\sum}}\frac{\mathrm{1}}{{n}}\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com