
Question Number 129562 by mathmax by abdo last updated on 16/Jan/21
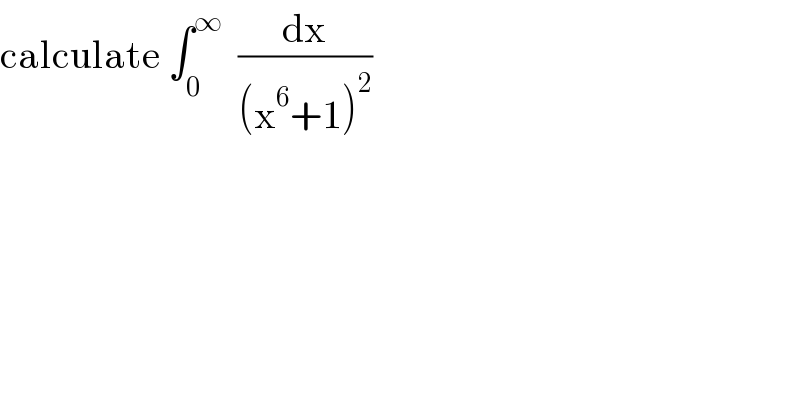
$$\mathrm{calculate}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{6}} +\mathrm{1}\right)^{\mathrm{2}} } \\ $$
Answered by Lordose last updated on 16/Jan/21
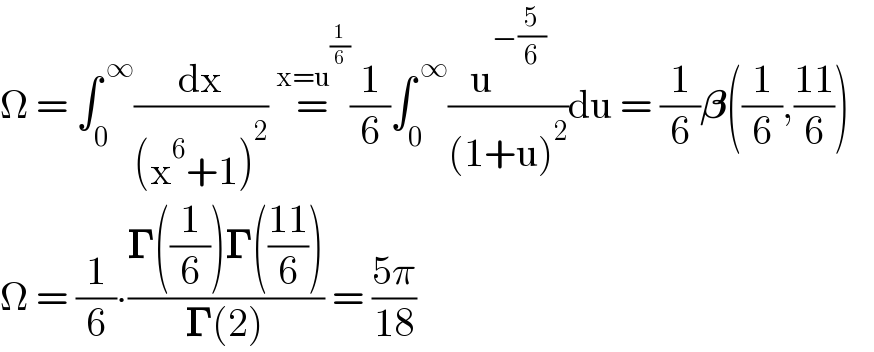
$$\Omega\:=\:\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{6}} +\mathrm{1}\right)^{\mathrm{2}} }\:\overset{\mathrm{x}=\mathrm{u}^{\frac{\mathrm{1}}{\mathrm{6}}} } {=}\frac{\mathrm{1}}{\mathrm{6}}\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{u}^{−\frac{\mathrm{5}}{\mathrm{6}}} }{\left(\mathrm{1}+\mathrm{u}\right)^{\mathrm{2}} }\mathrm{du}\:=\:\frac{\mathrm{1}}{\mathrm{6}}\boldsymbol{\beta}\left(\frac{\mathrm{1}}{\mathrm{6}},\frac{\mathrm{11}}{\mathrm{6}}\right)\:\:\: \\ $$$$\Omega\:=\:\frac{\mathrm{1}}{\mathrm{6}}\centerdot\frac{\boldsymbol{\Gamma}\left(\frac{\mathrm{1}}{\mathrm{6}}\right)\boldsymbol{\Gamma}\left(\frac{\mathrm{11}}{\mathrm{6}}\right)}{\boldsymbol{\Gamma}\left(\mathrm{2}\right)}\:=\:\frac{\mathrm{5}\pi}{\mathrm{18}} \\ $$
