
Question Number 138131 by mathmax by abdo last updated on 10/Apr/21
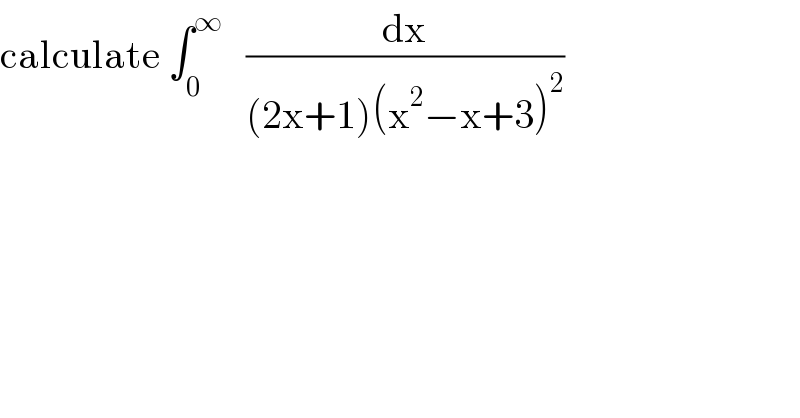
$$\mathrm{calculate}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{dx}}{\left(\mathrm{2x}+\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{3}\right)^{\mathrm{2}} } \\ $$
Answered by MJS_new last updated on 10/Apr/21
![∫(dx/((2x+1)(x^2 −x+3)^2 ))= [Ostrogradski] =((4x+9)/(165(x^2 −x+3)))+(8/(165))∫((x+6)/((2x+1)(x^2 −x+3)))dx= =((4x+9)/(165(x^2 −x+3)))+((16)/(225))∫(dx/(2x+1))−(8/(2475))∫((11x−24)/(x^2 −x+3))dx= =((4x+9)/(165(x^2 −x+3)))+(8/(225))ln ∣2x+1∣ −(4/(225))∫((2x−1)/(x^2 −x+3))dx+((148)/(2475))∫(dx/(x^2 −x+3))= =((4x+9)/(165(x^2 −x+3)))+(8/(225))ln ∣2x+1∣ −(4/(225))ln (x^2 −x+3) +((296(√(11)))/(27225))arctan ((2x−1)/( (√(11)))) +C answer is −(1/(55))+(4/(225))ln 12 +((148(√(11)))/(27225))π+((296(√(11)))/(27225))arctan ((√(11))/(11))](Q138174.png)
$$\int\frac{{dx}}{\left(\mathrm{2}{x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} −{x}+\mathrm{3}\right)^{\mathrm{2}} }= \\ $$$$\:\:\:\:\:\left[\mathrm{Ostrogradski}\right] \\ $$$$=\frac{\mathrm{4}{x}+\mathrm{9}}{\mathrm{165}\left({x}^{\mathrm{2}} −{x}+\mathrm{3}\right)}+\frac{\mathrm{8}}{\mathrm{165}}\int\frac{{x}+\mathrm{6}}{\left(\mathrm{2}{x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} −{x}+\mathrm{3}\right)}{dx}= \\ $$$$=\frac{\mathrm{4}{x}+\mathrm{9}}{\mathrm{165}\left({x}^{\mathrm{2}} −{x}+\mathrm{3}\right)}+\frac{\mathrm{16}}{\mathrm{225}}\int\frac{{dx}}{\mathrm{2}{x}+\mathrm{1}}−\frac{\mathrm{8}}{\mathrm{2475}}\int\frac{\mathrm{11}{x}−\mathrm{24}}{{x}^{\mathrm{2}} −{x}+\mathrm{3}}{dx}= \\ $$$$=\frac{\mathrm{4}{x}+\mathrm{9}}{\mathrm{165}\left({x}^{\mathrm{2}} −{x}+\mathrm{3}\right)}+\frac{\mathrm{8}}{\mathrm{225}}\mathrm{ln}\:\mid\mathrm{2}{x}+\mathrm{1}\mid\:−\frac{\mathrm{4}}{\mathrm{225}}\int\frac{\mathrm{2}{x}−\mathrm{1}}{{x}^{\mathrm{2}} −{x}+\mathrm{3}}{dx}+\frac{\mathrm{148}}{\mathrm{2475}}\int\frac{{dx}}{{x}^{\mathrm{2}} −{x}+\mathrm{3}}= \\ $$$$=\frac{\mathrm{4}{x}+\mathrm{9}}{\mathrm{165}\left({x}^{\mathrm{2}} −{x}+\mathrm{3}\right)}+\frac{\mathrm{8}}{\mathrm{225}}\mathrm{ln}\:\mid\mathrm{2}{x}+\mathrm{1}\mid\:−\frac{\mathrm{4}}{\mathrm{225}}\mathrm{ln}\:\left({x}^{\mathrm{2}} −{x}+\mathrm{3}\right)\:+\frac{\mathrm{296}\sqrt{\mathrm{11}}}{\mathrm{27225}}\mathrm{arctan}\:\frac{\mathrm{2}{x}−\mathrm{1}}{\:\sqrt{\mathrm{11}}}\:+{C} \\ $$$$\mathrm{answer}\:\mathrm{is}\:−\frac{\mathrm{1}}{\mathrm{55}}+\frac{\mathrm{4}}{\mathrm{225}}\mathrm{ln}\:\mathrm{12}\:+\frac{\mathrm{148}\sqrt{\mathrm{11}}}{\mathrm{27225}}\pi+\frac{\mathrm{296}\sqrt{\mathrm{11}}}{\mathrm{27225}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{11}}}{\mathrm{11}} \\ $$
Commented by MJS_new last updated on 10/Apr/21

$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome}!\:\mathrm{greetings}\:\mathrm{from}\:\mathrm{one}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{first}\:\mathrm{warm}\:\mathrm{spring}\:\mathrm{nights}\:\mathrm{in}\:\mathrm{Vienna}/\mathrm{Austria} \\ $$
Commented by mathmax by abdo last updated on 10/Apr/21

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}. \\ $$
