
Question Number 64745 by mathmax by abdo last updated on 21/Jul/19
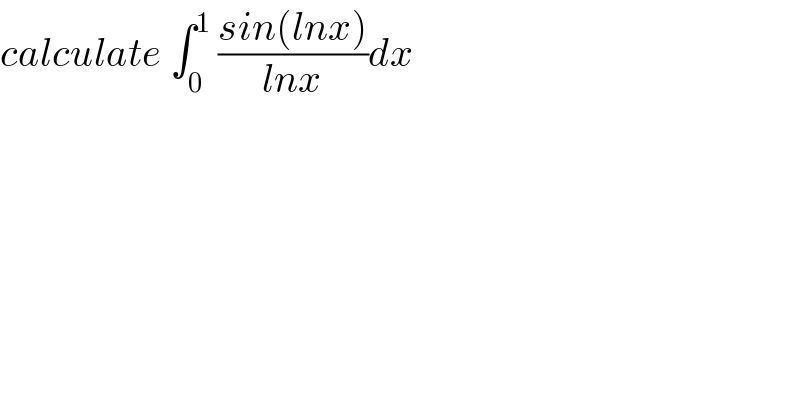
$${calculate}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{sin}\left({lnx}\right)}{{lnx}}{dx} \\ $$
Commented by mathmax by abdo last updated on 21/Jul/19
![let A =∫_0 ^1 ((sin(lnx))/(lnx))dx changement lnx =−t give x=e^(−t) A =−∫_0 ^∞ ((sin(−t))/(−t)) (−e^(−t) )dt = ∫_0 ^∞ ((sint)/t) e^(−t) dt let consider the parametric function ϕ(x) =∫_0 ^∞ ((sint)/t) e^(−xt) dt with x≥0 we have ϕ^′ (x) =−∫_0 ^∞ sint e^(−xt) dt =−Im(∫_0 ^∞ e^(it−xt) dt) ∫_0 ^∞ e^((−x+i)t) dt =[(1/(−x+i)) e^((−x+i)t) ]_0 ^(+∞) =−(1/(−x+i)) =(1/(x−i)) =((x+i)/(x^2 +1)) ⇒ϕ^′ (x)=−(1/(x^2 +1)) ⇒ϕ(x) =−arctan(x)+c ϕ(0) =(π/2) =c ⇒ϕ(x) =(π/2) −arctan(x) and ∫_0 ^∞ ((sint)/t) e^(−t) dt =ϕ(1) =(π/2) −(π/4) =(π/4) .](Q64789.png)
$${let}\:\:{A}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{sin}\left({lnx}\right)}{{lnx}}{dx}\:\:{changement}\:{lnx}\:=−{t}\:{give}\:{x}={e}^{−{t}} \\ $$$${A}\:=−\int_{\mathrm{0}} ^{\infty} \:\:\frac{{sin}\left(−{t}\right)}{−{t}}\:\left(−{e}^{−{t}} \right){dt}\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{sint}}{{t}}\:{e}^{−{t}} \:{dt}\:\:{let}\:{consider} \\ $$$${the}\:{parametric}\:{function}\:\:\varphi\left({x}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{sint}}{{t}}\:{e}^{−{xt}} {dt}\:{with}\:{x}\geqslant\mathrm{0} \\ $$$${we}\:{have}\:\varphi^{'} \left({x}\right)\:=−\int_{\mathrm{0}} ^{\infty} \:\:{sint}\:{e}^{−{xt}} {dt}\:\:=−{Im}\left(\int_{\mathrm{0}} ^{\infty} \:{e}^{{it}−{xt}} {dt}\right) \\ $$$$\int_{\mathrm{0}} ^{\infty} \:{e}^{\left(−{x}+{i}\right){t}} {dt}\:=\left[\frac{\mathrm{1}}{−{x}+{i}}\:{e}^{\left(−{x}+{i}\right){t}} \right]_{\mathrm{0}} ^{+\infty} \:=−\frac{\mathrm{1}}{−{x}+{i}}\:=\frac{\mathrm{1}}{{x}−{i}} \\ $$$$=\frac{{x}+{i}}{{x}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow\varphi^{'} \left({x}\right)=−\frac{\mathrm{1}}{{x}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow\varphi\left({x}\right)\:=−{arctan}\left({x}\right)+{c} \\ $$$$\varphi\left(\mathrm{0}\right)\:=\frac{\pi}{\mathrm{2}}\:={c}\:\Rightarrow\varphi\left({x}\right)\:=\frac{\pi}{\mathrm{2}}\:−{arctan}\left({x}\right)\:\:{and} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\frac{{sint}}{{t}}\:{e}^{−{t}} {dt}\:=\varphi\left(\mathrm{1}\right)\:=\frac{\pi}{\mathrm{2}}\:−\frac{\pi}{\mathrm{4}}\:=\frac{\pi}{\mathrm{4}}\:. \\ $$
