Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 208306 by SANOGO last updated on 10/Jun/24

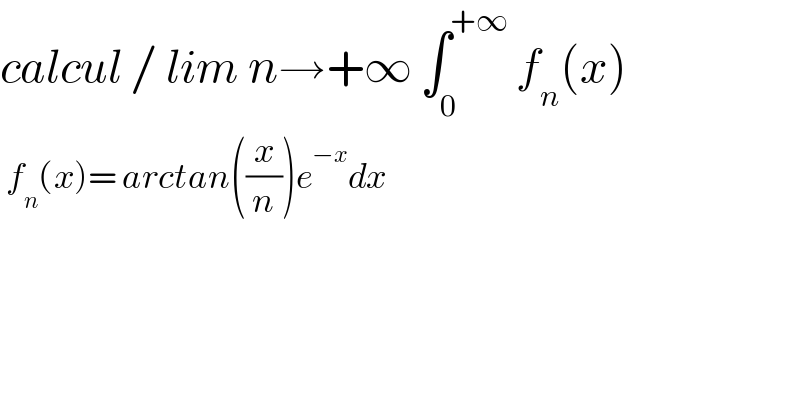
calcul / lim n→+∞ ∫_0 ^(+∞) f_n (x) f_n (x)= arctan((x/n))e^(−x) dx

$${calcul}\:/\:{lim}\:{n}\rightarrow+\infty\:\int_{\mathrm{0}} ^{+\infty} \:{f}_{{n}} \left({x}\right) \\ $$$$\:{f}_{{n}} \left({x}\right)=\:{arctan}\left(\frac{{x}}{{n}}\right){e}^{−{x}} {dx} \\ $$

Commented by SANOGO last updated on 11/Jun/24

thank you

$${thank}\:{you} \\ $$

Answered by Berbere last updated on 10/Jun/24

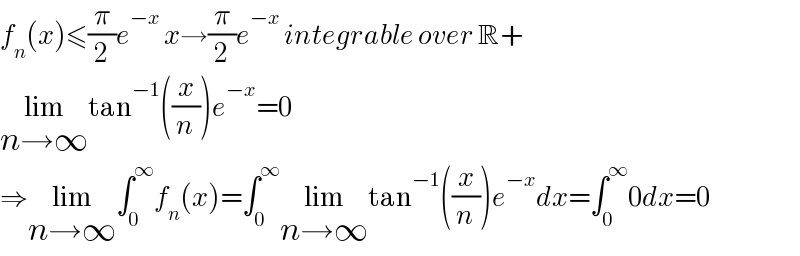
f_n (x)≤(π/2)e^(−x) x→(π/2)e^(−x) integrable over R+ lim_(n→∞) tan^(−1) ((x/n))e^(−x) =0 ⇒lim_(n→∞) ∫_0 ^∞ f_n (x)=∫_0 ^∞ lim_(n→∞) tan^(−1) ((x/n))e^(−x) dx=∫_0 ^∞ 0dx=0

$${f}_{{n}} \left({x}\right)\leqslant\frac{\pi}{\mathrm{2}}{e}^{−{x}} \:{x}\rightarrow\frac{\pi}{\mathrm{2}}{e}^{−{x}} \:{integrable}\:{over}\:\mathbb{R}+ \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}tan}^{−\mathrm{1}} \left(\frac{{x}}{{n}}\right){e}^{−{x}} =\mathrm{0} \\ $$$$\Rightarrow\underset{{n}\rightarrow\infty} {\mathrm{lim}}\int_{\mathrm{0}} ^{\infty} {f}_{{n}} \left({x}\right)=\int_{\mathrm{0}} ^{\infty} \underset{{n}\rightarrow\infty} {\mathrm{lim}tan}^{−\mathrm{1}} \left(\frac{{x}}{{n}}\right){e}^{−{x}} {dx}=\int_{\mathrm{0}} ^{\infty} \mathrm{0}{dx}=\mathrm{0} \\ $$

Answered by mathzup last updated on 10/Jun/24

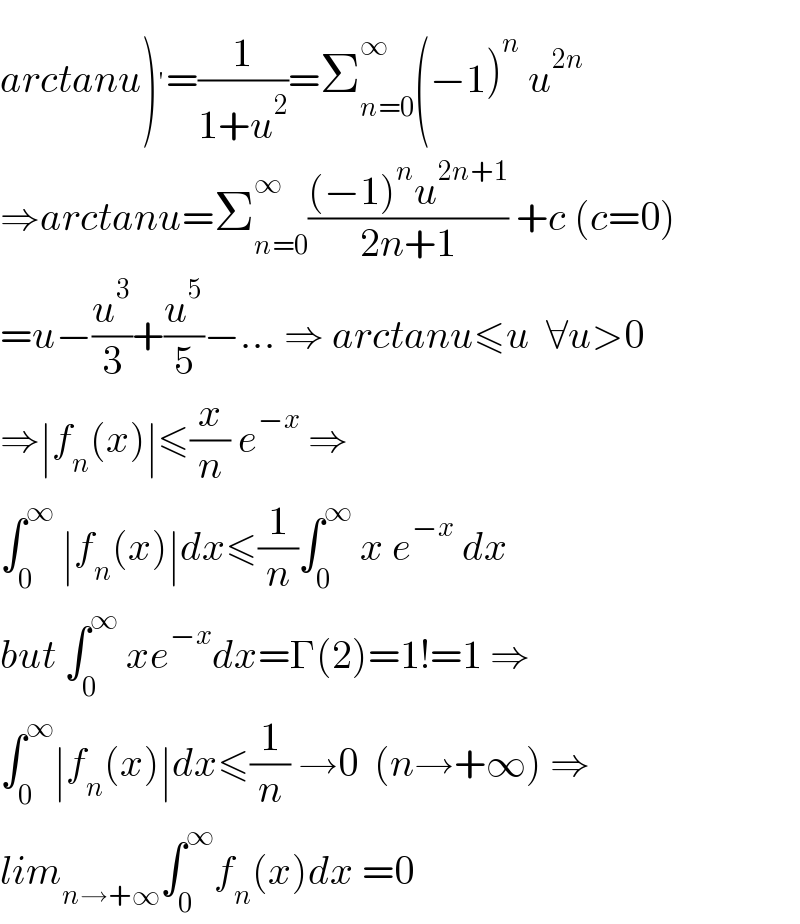
arctanu)^′ =(1/(1+u^2 ))=Σ_(n=0) ^∞ (−1)^n u^(2n) ⇒arctanu=Σ_(n=0) ^∞ (((−1)^n u^(2n+1) )/(2n+1)) +c (c=0) =u−(u^3 /3)+(u^5 /5)−... ⇒ arctanu≤u ∀u>0 ⇒∣f_n (x)∣≤(x/n) e^(−x) ⇒ ∫_0 ^∞ ∣f_n (x)∣dx≤(1/n)∫_0 ^∞ x e^(−x) dx but ∫_0 ^∞ xe^(−x) dx=Γ(2)=1!=1 ⇒ ∫_0 ^∞ ∣f_n (x)∣dx≤(1/n) →0 (n→+∞) ⇒ lim_(n→+∞) ∫_0 ^∞ f_n (x)dx =0

$$\left.{arctanu}\right)^{'} =\frac{\mathrm{1}}{\mathrm{1}+{u}^{\mathrm{2}} }=\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} \:{u}^{\mathrm{2}{n}} \\ $$$$\Rightarrow{arctanu}=\sum_{{n}=\mathrm{0}} ^{\infty} \frac{\left(−\mathrm{1}\right)^{{n}} {u}^{\mathrm{2}{n}+\mathrm{1}} }{\mathrm{2}{n}+\mathrm{1}}\:+{c}\:\left({c}=\mathrm{0}\right) \\ $$$$={u}−\frac{{u}^{\mathrm{3}} }{\mathrm{3}}+\frac{{u}^{\mathrm{5}} }{\mathrm{5}}−...\:\Rightarrow\:{arctanu}\leqslant{u}\:\:\forall{u}>\mathrm{0} \\ $$$$\Rightarrow\mid{f}_{{n}} \left({x}\right)\mid\leqslant\frac{{x}}{{n}}\:{e}^{−{x}} \:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\mid{f}_{{n}} \left({x}\right)\mid{dx}\leqslant\frac{\mathrm{1}}{{n}}\int_{\mathrm{0}} ^{\infty} \:{x}\:{e}^{−{x}} \:{dx} \\ $$$${but}\:\int_{\mathrm{0}} ^{\infty} \:{xe}^{−{x}} {dx}=\Gamma\left(\mathrm{2}\right)=\mathrm{1}!=\mathrm{1}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \mid{f}_{{n}} \left({x}\right)\mid{dx}\leqslant\frac{\mathrm{1}}{{n}}\:\rightarrow\mathrm{0}\:\:\left({n}\rightarrow+\infty\right)\:\Rightarrow \\ $$$${lim}_{{n}\rightarrow+\infty} \int_{\mathrm{0}} ^{\infty} {f}_{{n}} \left({x}\right){dx}\:=\mathrm{0} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com