Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 199236 by SANOGO last updated on 30/Oct/23

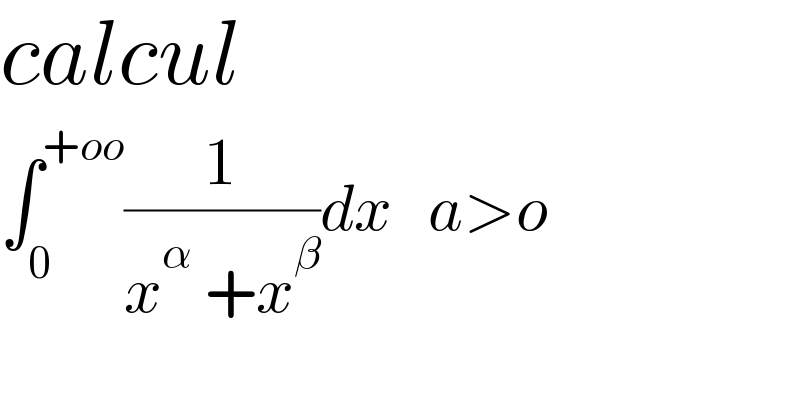
calcul ∫_0 ^(+oo) (1/(x^α +x^β ))dx a>o

$${calcul}\: \\ $$$$\int_{\mathrm{0}} ^{+{oo}} \frac{\mathrm{1}}{{x}^{\alpha} \:+{x}^{\beta} }{dx}\:\:\:{a}>{o} \\ $$

Answered by witcher3 last updated on 30/Oct/23

α≥β x^a +x^β =x^β (1+x^(a−𝛃) )∼x^β ,a−β≥0 integrable if β<1 x^a +x^β =x^a (1+x^(β−α) )∼x^a integrable if a>1,in ∞ f(a,b)=∫_0 ^∞ (dx/(x^a +x^b )), a>1>b ∫_0 ^∞ ((x^(−a) dx)/(1+x^(b−a) ))dx x^(b−a) =t⇒x=t^(1/(b−a)) =∫_∞ ^0 (t^(a/(a−b)) /(1+t)).(t^((1/(b−a))−1) /((b−a)))dt =(1/(a−b))∫_0 ^∞ (t^(((a−1)/(a−b))−1) /(1+t))dt β(x,y)=∫_0 ^∞ (t^(x−1) /((1+t)^(x+y) ))dx f(a,b)=(1/(a−b)).β(((a−1)/(a−b)),1−((a−1)/(a−b)))=(1/(a−b)).(π/(sin(π((a−1)/(a−b))))) f(a,b)=(π/((a−b)sin(((π(a−1))/(a−b)))));a>1>b

$$\alpha\geqslant\beta \\ $$$$\mathrm{x}^{\mathrm{a}} +\mathrm{x}^{\beta} =\mathrm{x}^{\beta} \left(\mathrm{1}+\mathrm{x}^{\mathrm{a}−\boldsymbol{\beta}} \right)\sim\mathrm{x}^{\beta} ,\mathrm{a}−\beta\geqslant\mathrm{0} \\ $$$$\mathrm{integrable}\:\mathrm{if}\:\beta<\mathrm{1} \\ $$$$\mathrm{x}^{\mathrm{a}} +\mathrm{x}^{\beta} =\mathrm{x}^{\mathrm{a}} \left(\mathrm{1}+\mathrm{x}^{\beta−\alpha} \right)\sim\mathrm{x}^{\mathrm{a}} \:\mathrm{integrable}\:\mathrm{if}\:\mathrm{a}>\mathrm{1},\mathrm{in}\:\infty \\ $$$$\mathrm{f}\left(\mathrm{a},\mathrm{b}\right)=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{a}} +\mathrm{x}^{\mathrm{b}} },\:\:\mathrm{a}>\mathrm{1}>\mathrm{b} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{x}^{−\mathrm{a}} \mathrm{dx}}{\mathrm{1}+\mathrm{x}^{\mathrm{b}−\mathrm{a}} }\mathrm{dx} \\ $$$$\mathrm{x}^{\mathrm{b}−\mathrm{a}} =\mathrm{t}\Rightarrow\mathrm{x}=\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{b}−\mathrm{a}}} \\ $$$$=\int_{\infty} ^{\mathrm{0}} \frac{\mathrm{t}^{\frac{\mathrm{a}}{\mathrm{a}−\mathrm{b}}} }{\mathrm{1}+\mathrm{t}}.\frac{\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{b}−\mathrm{a}}−\mathrm{1}} }{\left(\mathrm{b}−\mathrm{a}\right)}\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{a}−\mathrm{b}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{t}^{\frac{\mathrm{a}−\mathrm{1}}{\mathrm{a}−\mathrm{b}}−\mathrm{1}} }{\mathrm{1}+\mathrm{t}}\mathrm{dt} \\ $$$$\beta\left(\mathrm{x},\mathrm{y}\right)=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{t}^{\mathrm{x}−\mathrm{1}} }{\left(\mathrm{1}+\mathrm{t}\right)^{\mathrm{x}+\mathrm{y}} }\mathrm{dx} \\ $$$$\mathrm{f}\left(\mathrm{a},\mathrm{b}\right)=\frac{\mathrm{1}}{\mathrm{a}−\mathrm{b}}.\beta\left(\frac{\mathrm{a}−\mathrm{1}}{\mathrm{a}−\mathrm{b}},\mathrm{1}−\frac{\mathrm{a}−\mathrm{1}}{\mathrm{a}−\mathrm{b}}\right)=\frac{\mathrm{1}}{\mathrm{a}−\mathrm{b}}.\frac{\pi}{\mathrm{sin}\left(\pi\frac{\mathrm{a}−\mathrm{1}}{\mathrm{a}−\mathrm{b}}\right)} \\ $$$$\mathrm{f}\left(\mathrm{a},\mathrm{b}\right)=\frac{\pi}{\left(\mathrm{a}−\mathrm{b}\right)\mathrm{sin}\left(\frac{\pi\left(\mathrm{a}−\mathrm{1}\right)}{\mathrm{a}−\mathrm{b}}\right)};\mathrm{a}>\mathrm{1}>\mathrm{b} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com