
Question Number 205775 by SANOGO last updated on 30/Mar/24
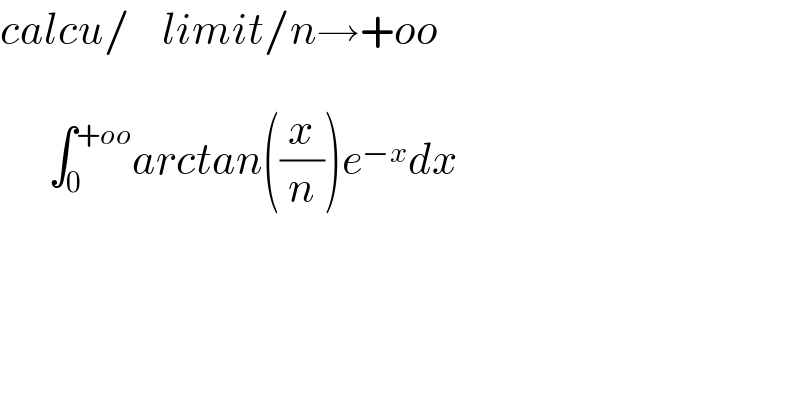
$${calcu}/\:\:\:\:{limit}/{n}\rightarrow+{oo} \\ $$$$\:\:\int_{\mathrm{0}} ^{+{oo}} {arctan}\left(\frac{{x}}{{n}}\right){e}^{−{x}} {dx} \\ $$
Answered by Berbere last updated on 30/Mar/24

$${U}_{{n}} \left({x}\right)=\mathrm{tan}^{−\mathrm{1}} \left(\frac{{x}}{{n}}\right){e}^{−{x}} \leqslant\frac{\pi}{\mathrm{2}}{e}^{−{x}} ;\forall{x}\in\mathbb{R}_{+} \\ $$$${x}\rightarrow\frac{\pi}{\mathrm{2}}{e}^{−{x}} ;{is}\:{Riemann}\:{integrabl}\:{over}\:\left[\mathrm{0},\infty\left[\right.\right. \\ $$$$\int_{\mathrm{0}} ^{\infty} \mathrm{tan}^{−\mathrm{1}} \left(\frac{{x}}{{n}}\right){e}^{−{x}} {dx}\leqslant\int_{\mathrm{0}} ^{\infty} \frac{\pi}{\mathrm{2}}{e}^{−{x}} =\frac{\pi}{\mathrm{2}} \\ $$$${domiate}\:{cv}\left[{Theorem}\Rightarrow\right. \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\int_{\mathrm{0}} ^{\infty} \mathrm{tan}^{−\mathrm{1}} \left(\frac{{x}}{{n}}\right){e}^{−{x}} {dx}=\int_{\mathrm{0}} ^{\infty} \underset{{n}\rightarrow\infty} {\mathrm{lim}tan}^{−\mathrm{1}} \left(\frac{{x}}{{n}}\right){e}^{−{x}} {dx}=\mathrm{0} \\ $$$${or}\:{using}\:\mathrm{0}\leqslant\mathrm{tan}^{−\mathrm{1}} \left({x}\right)\leqslant{x} \\ $$$$\mathrm{tan}^{−\mathrm{1}} \left({x}\right)=\int_{\mathrm{0}} ^{{x}} \frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\leqslant\int_{\mathrm{0}} ^{{x}} {dt}={x} \\ $$$$\Rightarrow\mathrm{0}\leqslant\mathrm{tan}^{−\mathrm{1}} \left(\frac{{x}}{{n}}\right){e}^{−{x}} \leqslant\frac{{x}}{{n}}{e}^{−{x}} \\ $$$$\mathrm{0}\leqslant\int_{\mathrm{0}} ^{\infty} \mathrm{tan}^{−\mathrm{1}} \left(\frac{{x}}{{n}}\right){e}^{−{x}} \leqslant\frac{\mathrm{1}}{{n}}\int_{\mathrm{0}} ^{\infty} {xe}^{−{x}} {dx}=\frac{\mathrm{1}}{{n}}\Gamma\left(\mathrm{2}\right)_{\rightarrow\mathrm{0}} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\int_{\mathrm{0}} ^{\infty} \mathrm{tan}^{−\mathrm{1}} \left(\frac{{x}}{{n}}\right){e}^{−{x}} {dx}=\mathrm{0} \\ $$$$ \\ $$
