
Question Number 117493 by bobhans last updated on 12/Oct/20
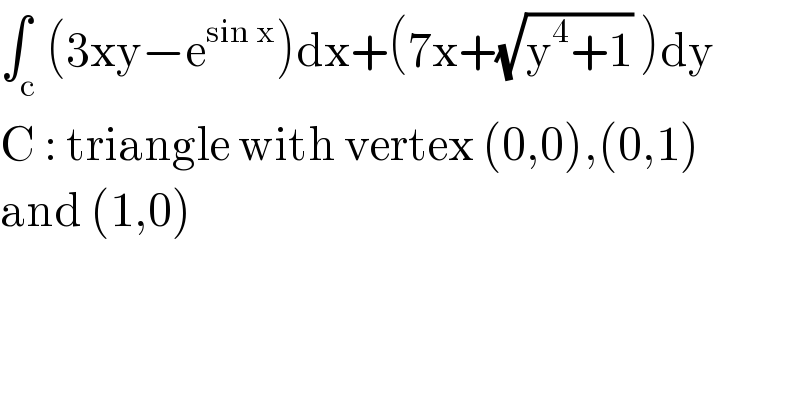
$$\int_{\mathrm{c}} \left(\mathrm{3xy}−\mathrm{e}^{\mathrm{sin}\:\mathrm{x}} \right)\mathrm{dx}+\left(\mathrm{7x}+\sqrt{\mathrm{y}^{\mathrm{4}} +\mathrm{1}}\:\right)\mathrm{dy} \\ $$$$\mathrm{C}\::\:\mathrm{triangle}\:\mathrm{with}\:\mathrm{vertex}\:\left(\mathrm{0},\mathrm{0}\right),\left(\mathrm{0},\mathrm{1}\right) \\ $$$$\mathrm{and}\:\left(\mathrm{1},\mathrm{0}\right) \\ $$
Answered by bemath last updated on 12/Oct/20
![Green Theorem ∫_c Pdx+Qdy=∫∫_D (Q_x −P_y )dxdy =∫∫_D (7−3x)dxdy =∫_0 ^1 ∫_0 ^(1−x) (7−3x)dydx = ∫_0 ^1 (7−3x)(1−x) dx = ∫_0 ^1 (7−10x+3x^2 )dx =[ 7x−5x^2 +x^3 ]_0 ^1 = 3](Q117494.png)
$$\mathrm{Green}\:\mathrm{Theorem} \\ $$$$\int_{\mathrm{c}} \mathrm{Pdx}+\mathrm{Qdy}=\int\int_{\mathrm{D}} \left(\mathrm{Q}_{\mathrm{x}} −\mathrm{P}_{\mathrm{y}} \right)\mathrm{dxdy} \\ $$$$=\int\int_{\mathrm{D}} \left(\mathrm{7}−\mathrm{3x}\right)\mathrm{dxdy} \\ $$$$=\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\:\underset{\mathrm{0}} {\overset{\mathrm{1}−\mathrm{x}} {\int}}\:\left(\mathrm{7}−\mathrm{3x}\right)\mathrm{dydx} \\ $$$$=\:\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\left(\mathrm{7}−\mathrm{3x}\right)\left(\mathrm{1}−\mathrm{x}\right)\:\mathrm{dx} \\ $$$$=\:\overset{\mathrm{1}} {\int}_{\mathrm{0}} \left(\mathrm{7}−\mathrm{10x}+\mathrm{3x}^{\mathrm{2}} \right)\mathrm{dx} \\ $$$$=\left[\:\mathrm{7x}−\mathrm{5x}^{\mathrm{2}} +\mathrm{x}^{\mathrm{3}} \:\right]_{\mathrm{0}} ^{\mathrm{1}} \:=\:\mathrm{3} \\ $$
