
Question Number 139371 by mohammad17 last updated on 26/Apr/21

$${by}\:{use}\:{Gamma}\:{function}\:{prove}\: \\ $$$$ \\ $$$$\left(\mathrm{1}\right)\:\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{8}}} {cos}^{\mathrm{3}} \mathrm{4}{xdx}=\frac{\mathrm{1}}{\mathrm{6}} \\ $$$$ \\ $$$$\left(\mathrm{2}\right)\:\int_{\mathrm{0}} ^{\:\pi} {sin}^{\mathrm{6}} \left(\frac{{x}}{\mathrm{2}}\right){cos}^{\mathrm{8}} \left(\frac{{x}}{\mathrm{2}}\right){dx}=\frac{\mathrm{5}\pi}{\mathrm{2}^{\mathrm{11}} } \\ $$
Answered by Dwaipayan Shikari last updated on 26/Apr/21
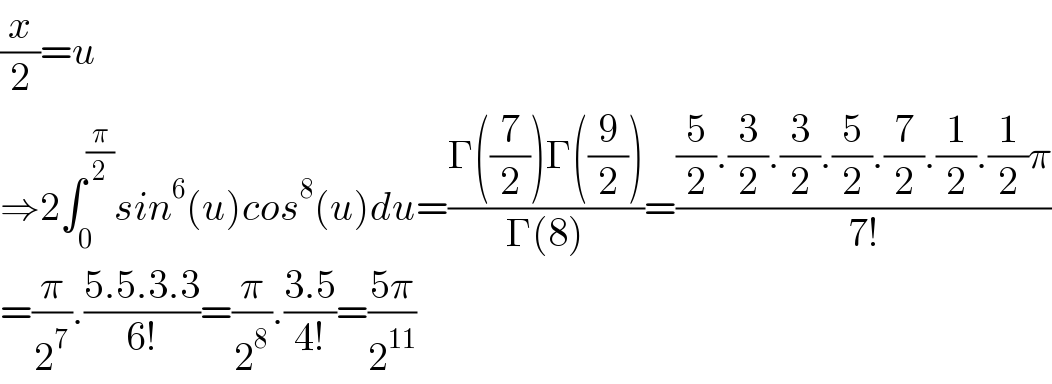
$$\frac{{x}}{\mathrm{2}}={u} \\ $$$$\Rightarrow\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {sin}^{\mathrm{6}} \left({u}\right){cos}^{\mathrm{8}} \left({u}\right){du}=\frac{\Gamma\left(\frac{\mathrm{7}}{\mathrm{2}}\right)\Gamma\left(\frac{\mathrm{9}}{\mathrm{2}}\right)}{\Gamma\left(\mathrm{8}\right)}=\frac{\frac{\mathrm{5}}{\mathrm{2}}.\frac{\mathrm{3}}{\mathrm{2}}.\frac{\mathrm{3}}{\mathrm{2}}.\frac{\mathrm{5}}{\mathrm{2}}.\frac{\mathrm{7}}{\mathrm{2}}.\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{1}}{\mathrm{2}}\pi}{\mathrm{7}!} \\ $$$$=\frac{\pi}{\mathrm{2}^{\mathrm{7}} }.\frac{\mathrm{5}.\mathrm{5}.\mathrm{3}.\mathrm{3}}{\mathrm{6}!}=\frac{\pi}{\mathrm{2}^{\mathrm{8}} }.\frac{\mathrm{3}.\mathrm{5}}{\mathrm{4}!}=\frac{\mathrm{5}\pi}{\mathrm{2}^{\mathrm{11}} } \\ $$
Commented by mohammad17 last updated on 26/Apr/21
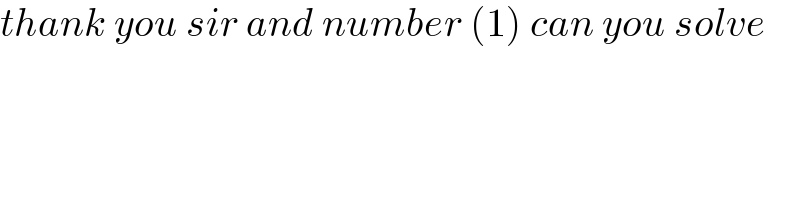
$${thank}\:{you}\:{sir}\:{and}\:{number}\:\left(\mathrm{1}\right)\:{can}\:{you}\:{solve} \\ $$
Answered by Dwaipayan Shikari last updated on 26/Apr/21
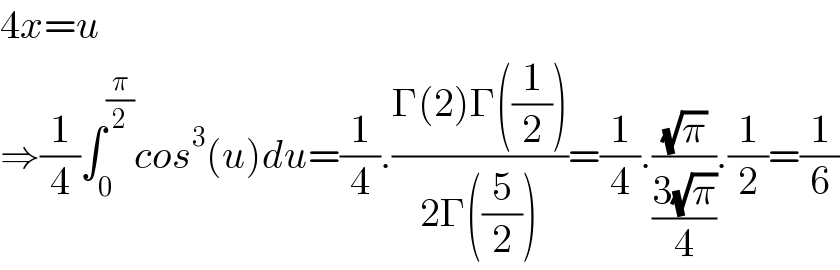
$$\mathrm{4}{x}={u} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cos}^{\mathrm{3}} \left({u}\right){du}=\frac{\mathrm{1}}{\mathrm{4}}.\frac{\Gamma\left(\mathrm{2}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\mathrm{2}\Gamma\left(\frac{\mathrm{5}}{\mathrm{2}}\right)}=\frac{\mathrm{1}}{\mathrm{4}}.\frac{\sqrt{\pi}}{\frac{\mathrm{3}\sqrt{\pi}}{\mathrm{4}}}.\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{6}} \\ $$
Commented by mohammad17 last updated on 26/Apr/21
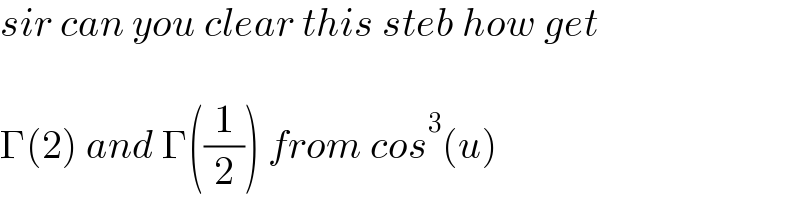
$${sir}\:{can}\:{you}\:{clear}\:{this}\:{steb}\:{how}\:{get} \\ $$$$ \\ $$$$\Gamma\left(\mathrm{2}\right)\:{and}\:\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\:{from}\:{cos}^{\mathrm{3}} \left({u}\right) \\ $$
Commented by mohammad17 last updated on 26/Apr/21

$${thank}\:{you}\:{sir} \\ $$
Commented by Dwaipayan Shikari last updated on 26/Apr/21
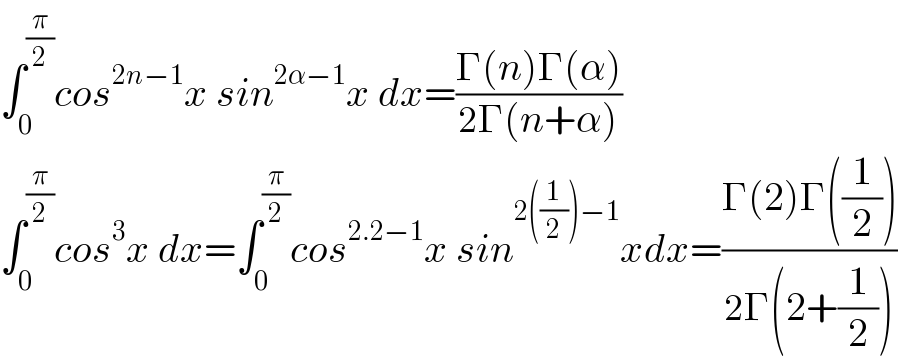
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cos}^{\mathrm{2}{n}−\mathrm{1}} {x}\:{sin}^{\mathrm{2}\alpha−\mathrm{1}} {x}\:{dx}=\frac{\Gamma\left({n}\right)\Gamma\left(\alpha\right)}{\mathrm{2}\Gamma\left({n}+\alpha\right)} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cos}^{\mathrm{3}} {x}\:{dx}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cos}^{\mathrm{2}.\mathrm{2}−\mathrm{1}} {x}\:{sin}^{\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\mathrm{1}} {xdx}=\frac{\Gamma\left(\mathrm{2}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\mathrm{2}\Gamma\left(\mathrm{2}+\frac{\mathrm{1}}{\mathrm{2}}\right)} \\ $$
Answered by Ar Brandon last updated on 26/Apr/21
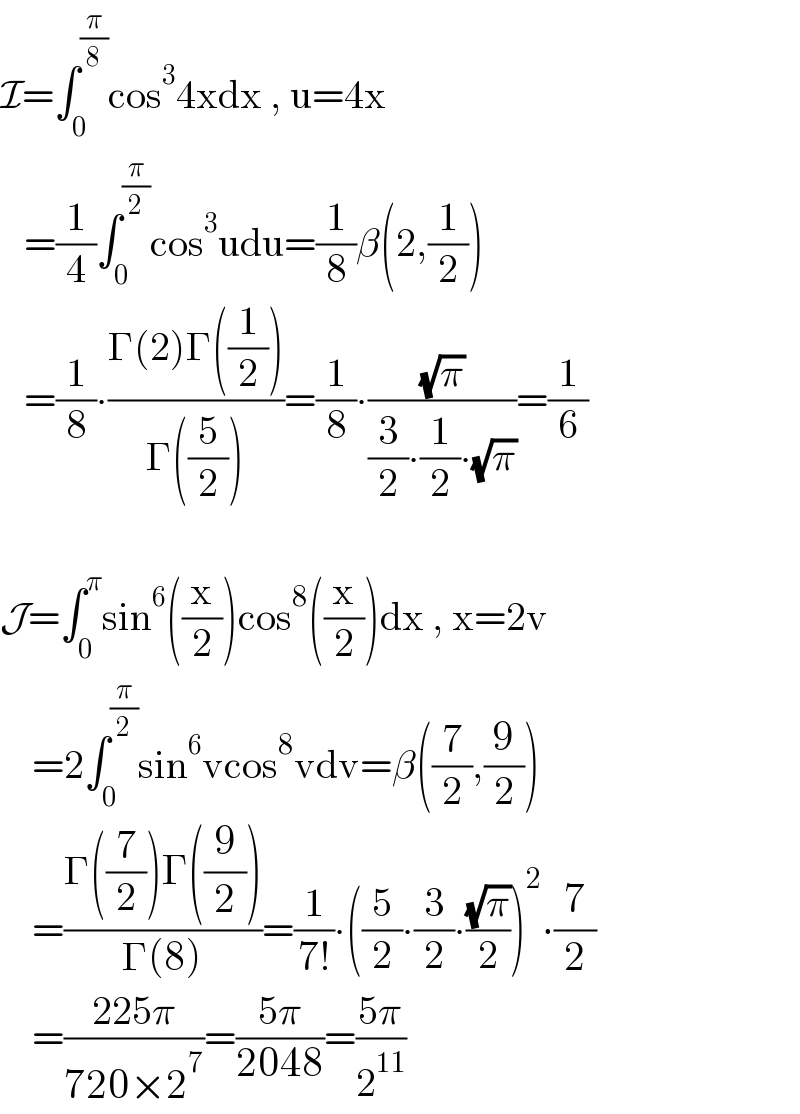
$$\mathcal{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{8}}} \mathrm{cos}^{\mathrm{3}} \mathrm{4xdx}\:,\:\mathrm{u}=\mathrm{4x} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{cos}^{\mathrm{3}} \mathrm{udu}=\frac{\mathrm{1}}{\mathrm{8}}\beta\left(\mathrm{2},\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{8}}\centerdot\frac{\Gamma\left(\mathrm{2}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\Gamma\left(\frac{\mathrm{5}}{\mathrm{2}}\right)}=\frac{\mathrm{1}}{\mathrm{8}}\centerdot\frac{\sqrt{\pi}}{\frac{\mathrm{3}}{\mathrm{2}}\centerdot\frac{\mathrm{1}}{\mathrm{2}}\centerdot\sqrt{\pi}}=\frac{\mathrm{1}}{\mathrm{6}} \\ $$$$ \\ $$$$\mathcal{J}=\int_{\mathrm{0}} ^{\pi} \mathrm{sin}^{\mathrm{6}} \left(\frac{\mathrm{x}}{\mathrm{2}}\right)\mathrm{cos}^{\mathrm{8}} \left(\frac{\mathrm{x}}{\mathrm{2}}\right)\mathrm{dx}\:,\:\mathrm{x}=\mathrm{2v} \\ $$$$\:\:\:\:=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sin}^{\mathrm{6}} \mathrm{vcos}^{\mathrm{8}} \mathrm{vdv}=\beta\left(\frac{\mathrm{7}}{\mathrm{2}},\frac{\mathrm{9}}{\mathrm{2}}\right) \\ $$$$\:\:\:\:=\frac{\Gamma\left(\frac{\mathrm{7}}{\mathrm{2}}\right)\Gamma\left(\frac{\mathrm{9}}{\mathrm{2}}\right)}{\Gamma\left(\mathrm{8}\right)}=\frac{\mathrm{1}}{\mathrm{7}!}\centerdot\left(\frac{\mathrm{5}}{\mathrm{2}}\centerdot\frac{\mathrm{3}}{\mathrm{2}}\centerdot\frac{\sqrt{\pi}}{\mathrm{2}}\right)^{\mathrm{2}} \centerdot\frac{\mathrm{7}}{\mathrm{2}} \\ $$$$\:\:\:\:=\frac{\mathrm{225}\pi}{\mathrm{720}×\mathrm{2}^{\mathrm{7}} }=\frac{\mathrm{5}\pi}{\mathrm{2048}}=\frac{\mathrm{5}\pi}{\mathrm{2}^{\mathrm{11}} } \\ $$
