Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 192957 by York12 last updated on 31/May/23

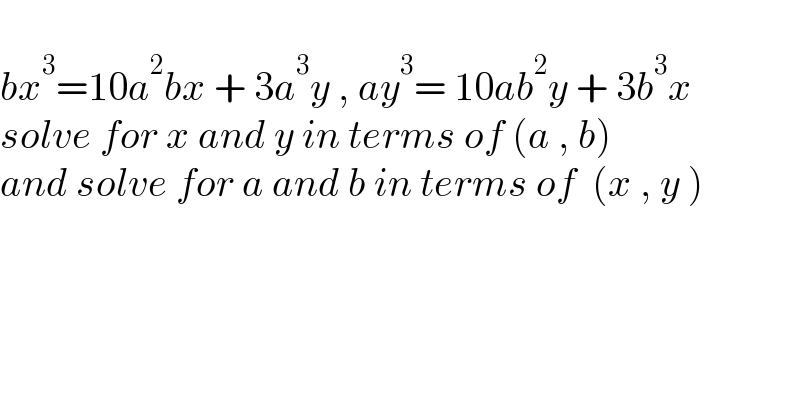
bx^3 =10a^2 bx + 3a^3 y , ay^3 = 10ab^2 y + 3b^3 x solve for x and y in terms of (a , b) and solve for a and b in terms of (x , y )

$$ \\ $$$${bx}^{\mathrm{3}} =\mathrm{10}{a}^{\mathrm{2}} {bx}\:+\:\mathrm{3}{a}^{\mathrm{3}} {y}\:,\:{ay}^{\mathrm{3}} =\:\mathrm{10}{ab}^{\mathrm{2}} {y}\:+\:\mathrm{3}{b}^{\mathrm{3}} {x} \\ $$$${solve}\:{for}\:{x}\:{and}\:{y}\:{in}\:{terms}\:{of}\:\left({a}\:,\:{b}\right) \\ $$$${and}\:{solve}\:{for}\:{a}\:{and}\:{b}\:{in}\:{terms}\:{of}\:\:\left({x}\:,\:{y}\:\right) \\ $$

Commented by York12 last updated on 02/Jun/23

Commented by York12 last updated on 02/Jun/23

no common roots means no existence for any value of x which can satify both equations ⇒ your system of equations is again wrong

$${no}\:{common}\:{roots} \\ $$$${means}\:{no}\:{existence}\:{for}\:{any}\:{value} \\ $$$${of}\:{x}\:{which}\:{can}\:{satify}\:{both}\:{equations} \\ $$$$\Rightarrow\:{your}\:{system}\:{of}\:\:{equations}\:{is}\:{again} \\ $$$${wrong}\: \\ $$

Answered by a.lgnaoui last updated on 01/Jun/23

{ ((bx^3 −10a^2 bx=3a^3 y⇒ y=((xb(x^2 −10a^2 ))/(3a^3 )) (1))),((3b^3 x=ay^3 −10ab^2 y⇒ x=((ya(y^2 −10b^2 ))/(3b^3 )) (2))) :} y^2 =((x^2 b^2 (x^2 −10a^2 )^2 )/(9a^6 )) x^2 =((y^2 a^2 (y^2 −10b^2 ))/(9b^6 )) (1)⇔y=(b/(3a^3 ))[((ya(y^2 −10b^2 )/(3b^3 ))][(((y^2 a^2 (y^2 −10b^2 )−90a^2 b^6 )/(9b^6 ))] 81a^3 b^9 y=ab(y^2 −10b^2 )(a^2 y^4 −10y^2 a^2 b^2 −90a^2 b^6 ) =a^3 b(y^2 −10b^2 )(y^4 −10y^2 b^2 −90b^6 ) =a^3 b[y^6 −10y^4 b^2 −90y^2 b^6 −10b^2 y^4 +100b^4 y^2 +900b^8 =a^3 b[y^6 −20b^2 y^4 −(90b^6 −100b^4 )y^2 +900b^8 ] =81a^3 b^9 y ⇒81b^8 y=y^6 −20b^2 y^4 −10b^4 (9b^2 −10)y^2 +900b^8 ⇒y^6 −20b^2 [y^4 −(1/2)(9b^2 −10)b^2 y^2 +45b^6 ]−81b^8 y=0 =y^6 −20b^2 (y^2 −(((9b^2 −10)b^2 )/4))^2 −81b^8 y+45b^6 −(((9b^2 −10)b^4 )/(16))=0 ..........to continious

$$\begin{cases}{\mathrm{bx}^{\mathrm{3}} −\mathrm{10a}^{\mathrm{2}} \mathrm{bx}=\mathrm{3a}^{\mathrm{3}} \mathrm{y}\Rightarrow\:\:\:\boldsymbol{\mathrm{y}}=\frac{\boldsymbol{\mathrm{xb}}\left(\boldsymbol{\mathrm{x}}^{\mathrm{2}} −\mathrm{10}\boldsymbol{\mathrm{a}}^{\mathrm{2}} \right)}{\mathrm{3}\boldsymbol{\mathrm{a}}^{\mathrm{3}} }\:\left(\mathrm{1}\right)}\\{\mathrm{3b}^{\mathrm{3}} \mathrm{x}=\mathrm{ay}^{\mathrm{3}} −\mathrm{10ab}^{\mathrm{2}} \mathrm{y}\Rightarrow\:\:\boldsymbol{\mathrm{x}}=\frac{\boldsymbol{\mathrm{ya}}\left(\boldsymbol{\mathrm{y}}^{\mathrm{2}} −\mathrm{10}\boldsymbol{\mathrm{b}}^{\mathrm{2}} \right)}{\mathrm{3}\boldsymbol{\mathrm{b}}^{\mathrm{3}} }\:\:\left(\mathrm{2}\right)}\end{cases} \\ $$$$\boldsymbol{\mathrm{y}}^{\mathrm{2}} =\frac{\boldsymbol{\mathrm{x}}^{\mathrm{2}} \boldsymbol{\mathrm{b}}^{\mathrm{2}} \left(\boldsymbol{\mathrm{x}}^{\mathrm{2}} −\mathrm{10}\boldsymbol{\mathrm{a}}^{\mathrm{2}} \right)^{\mathrm{2}} }{\mathrm{9}\boldsymbol{\mathrm{a}}^{\mathrm{6}} } \\ $$$$\boldsymbol{\mathrm{x}}^{\mathrm{2}} =\frac{\boldsymbol{\mathrm{y}}^{\mathrm{2}} \boldsymbol{\mathrm{a}}^{\mathrm{2}} \left(\boldsymbol{\mathrm{y}}^{\mathrm{2}} −\mathrm{10}\boldsymbol{\mathrm{b}}^{\mathrm{2}} \right)}{\mathrm{9}\boldsymbol{\mathrm{b}}^{\mathrm{6}} } \\ $$$$\left(\mathrm{1}\right)\Leftrightarrow\boldsymbol{\mathrm{y}}=\frac{\boldsymbol{\mathrm{b}}}{\mathrm{3}\boldsymbol{\mathrm{a}}^{\mathrm{3}} }\left[\frac{\boldsymbol{\mathrm{ya}}\left(\boldsymbol{\mathrm{y}}^{\mathrm{2}} −\mathrm{10}\boldsymbol{\mathrm{b}}^{\mathrm{2}} \right.}{\mathrm{3}\boldsymbol{\mathrm{b}}^{\mathrm{3}} }\right]\left[\left(\frac{\boldsymbol{\mathrm{y}}^{\mathrm{2}} \boldsymbol{\mathrm{a}}^{\mathrm{2}} \left(\boldsymbol{\mathrm{y}}^{\mathrm{2}} −\mathrm{10}\boldsymbol{\mathrm{b}}^{\mathrm{2}} \right)−\mathrm{90}\boldsymbol{\mathrm{a}}^{\mathrm{2}} \boldsymbol{\mathrm{b}}^{\mathrm{6}} }{\mathrm{9}\boldsymbol{\mathrm{b}}^{\mathrm{6}} }\right]\right. \\ $$$$\mathrm{81}\boldsymbol{\mathrm{a}}^{\mathrm{3}} \boldsymbol{\mathrm{b}}^{\mathrm{9}} \boldsymbol{\mathrm{y}}=\boldsymbol{\mathrm{ab}}\left(\boldsymbol{\mathrm{y}}^{\mathrm{2}} −\mathrm{10}\boldsymbol{\mathrm{b}}^{\mathrm{2}} \right)\left(\boldsymbol{\mathrm{a}}^{\mathrm{2}} \boldsymbol{\mathrm{y}}^{\mathrm{4}} −\mathrm{10}\boldsymbol{\mathrm{y}}^{\mathrm{2}} \boldsymbol{\mathrm{a}}^{\mathrm{2}} \boldsymbol{\mathrm{b}}^{\mathrm{2}} −\mathrm{90}\boldsymbol{\mathrm{a}}^{\mathrm{2}} \boldsymbol{\mathrm{b}}^{\mathrm{6}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\boldsymbol{\mathrm{a}}^{\mathrm{3}} \boldsymbol{\mathrm{b}}\left(\boldsymbol{\mathrm{y}}^{\mathrm{2}} −\mathrm{10}\boldsymbol{\mathrm{b}}^{\mathrm{2}} \right)\left(\boldsymbol{\mathrm{y}}^{\mathrm{4}} −\mathrm{10}\boldsymbol{\mathrm{y}}^{\mathrm{2}} \boldsymbol{\mathrm{b}}^{\mathrm{2}} −\mathrm{90}\boldsymbol{\mathrm{b}}^{\mathrm{6}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\boldsymbol{\mathrm{a}}^{\mathrm{3}} \boldsymbol{\mathrm{b}}\left[\boldsymbol{\mathrm{y}}^{\mathrm{6}} −\mathrm{10}\boldsymbol{\mathrm{y}}^{\mathrm{4}} \boldsymbol{\mathrm{b}}^{\mathrm{2}} −\mathrm{90}\boldsymbol{\mathrm{y}}^{\mathrm{2}} \boldsymbol{\mathrm{b}}^{\mathrm{6}} \right. \\ $$$$\:\:\:−\mathrm{10}\boldsymbol{\mathrm{b}}^{\mathrm{2}} \boldsymbol{\mathrm{y}}^{\mathrm{4}} +\mathrm{100}\boldsymbol{\mathrm{b}}^{\mathrm{4}} \boldsymbol{\mathrm{y}}^{\mathrm{2}} +\mathrm{900}\boldsymbol{\mathrm{b}}^{\mathrm{8}} \\ $$$$=\boldsymbol{\mathrm{a}}^{\mathrm{3}} \boldsymbol{\mathrm{b}}\left[\boldsymbol{\mathrm{y}}^{\mathrm{6}} −\mathrm{20}\boldsymbol{\mathrm{b}}^{\mathrm{2}} \boldsymbol{\mathrm{y}}^{\mathrm{4}} −\left(\mathrm{90}\boldsymbol{\mathrm{b}}^{\mathrm{6}} −\mathrm{100}\boldsymbol{\mathrm{b}}^{\mathrm{4}} \right)\boldsymbol{\mathrm{y}}^{\mathrm{2}} +\mathrm{900}\boldsymbol{\mathrm{b}}^{\mathrm{8}} \right] \\ $$$$=\mathrm{81}\boldsymbol{\mathrm{a}}^{\mathrm{3}} \boldsymbol{\mathrm{b}}^{\mathrm{9}} \boldsymbol{\mathrm{y}} \\ $$$$ \\ $$$$\Rightarrow\mathrm{81b}^{\mathrm{8}} \boldsymbol{\mathrm{y}}=\boldsymbol{\mathrm{y}}^{\mathrm{6}} −\mathrm{20}\boldsymbol{\mathrm{b}}^{\mathrm{2}} \boldsymbol{\mathrm{y}}^{\mathrm{4}} −\mathrm{10}\boldsymbol{\mathrm{b}}^{\mathrm{4}} \left(\mathrm{9}\boldsymbol{\mathrm{b}}^{\mathrm{2}} −\mathrm{10}\right)\boldsymbol{\mathrm{y}}^{\mathrm{2}} +\mathrm{900}\boldsymbol{\mathrm{b}}^{\mathrm{8}} \\ $$$$\Rightarrow\boldsymbol{\mathrm{y}}^{\mathrm{6}} −\mathrm{20}\boldsymbol{\mathrm{b}}^{\mathrm{2}} \left[\boldsymbol{\mathrm{y}}^{\mathrm{4}} −\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{9}\boldsymbol{\mathrm{b}}^{\mathrm{2}} −\mathrm{10}\right)\boldsymbol{\mathrm{b}}^{\mathrm{2}} \boldsymbol{\mathrm{y}}^{\mathrm{2}} +\mathrm{45}\boldsymbol{\mathrm{b}}^{\mathrm{6}} \right]−\mathrm{81}\boldsymbol{\mathrm{b}}^{\mathrm{8}} \boldsymbol{\mathrm{y}}=\mathrm{0} \\ $$$$=\boldsymbol{\mathrm{y}}^{\mathrm{6}} −\mathrm{20}\boldsymbol{\mathrm{b}}^{\mathrm{2}} \left(\boldsymbol{\mathrm{y}}^{\mathrm{2}} −\frac{\left(\mathrm{9}\boldsymbol{\mathrm{b}}^{\mathrm{2}} −\mathrm{10}\right)\boldsymbol{\mathrm{b}}^{\mathrm{2}} }{\mathrm{4}}\right)^{\mathrm{2}} −\mathrm{81}\boldsymbol{\mathrm{b}}^{\mathrm{8}} \boldsymbol{\mathrm{y}}+\mathrm{45}\boldsymbol{\mathrm{b}}^{\mathrm{6}} −\frac{\left(\mathrm{9}\boldsymbol{\mathrm{b}}^{\mathrm{2}} −\mathrm{10}\right)\boldsymbol{\mathrm{b}}^{\mathrm{4}} }{\mathrm{16}}=\mathrm{0} \\ $$$$..........\boldsymbol{\mathrm{to}}\:\boldsymbol{\mathrm{continious}} \\ $$$$ \\ $$

Answered by Frix last updated on 01/Jun/23

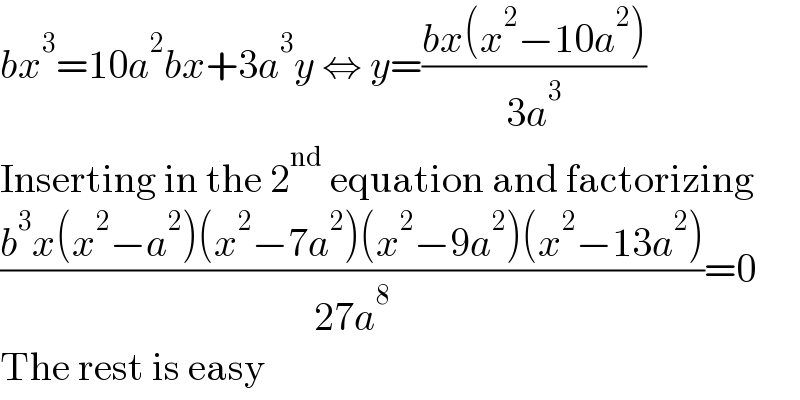
bx^3 =10a^2 bx+3a^3 y ⇔ y=((bx(x^2 −10a^2 ))/(3a^3 )) Inserting in the 2^(nd) equation and factorizing ((b^3 x(x^2 −a^2 )(x^2 −7a^2 )(x^2 −9a^2 )(x^2 −13a^2 ))/(27a^8 ))=0 The rest is easy

$${bx}^{\mathrm{3}} =\mathrm{10}{a}^{\mathrm{2}} {bx}+\mathrm{3}{a}^{\mathrm{3}} {y}\:\Leftrightarrow\:{y}=\frac{{bx}\left({x}^{\mathrm{2}} −\mathrm{10}{a}^{\mathrm{2}} \right)}{\mathrm{3}{a}^{\mathrm{3}} } \\ $$$$\mathrm{Inserting}\:\mathrm{in}\:\mathrm{the}\:\mathrm{2}^{\mathrm{nd}} \:\mathrm{equation}\:\mathrm{and}\:\mathrm{factorizing} \\ $$$$\frac{{b}^{\mathrm{3}} {x}\left({x}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)\left({x}^{\mathrm{2}} −\mathrm{7}{a}^{\mathrm{2}} \right)\left({x}^{\mathrm{2}} −\mathrm{9}{a}^{\mathrm{2}} \right)\left({x}^{\mathrm{2}} −\mathrm{13}{a}^{\mathrm{2}} \right)}{\mathrm{27}{a}^{\mathrm{8}} }=\mathrm{0} \\ $$$$\mathrm{The}\:\mathrm{rest}\:\mathrm{is}\:\mathrm{easy} \\ $$

Commented by York12 last updated on 01/Jun/23

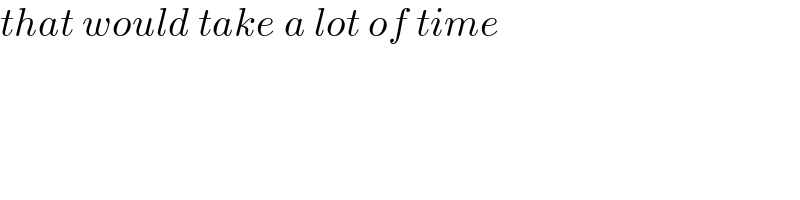
that would take a lot of time

$${that}\:{would}\:{take}\:{a}\:{lot}\:{of}\:{time} \\ $$$$ \\ $$

Commented by York12 last updated on 01/Jun/23

watch this

$${watch}\:{this} \\ $$

Answered by a.lgnaoui last updated on 01/Jun/23

(suite) { ((bx^3 −10ba^2 x=3a^3 y ⇒b=((3a^3 y)/(x(x^2 −10a^2 ))) (1))),((ay^3 −10ab^2 y=3b^3 x ⇒a=((3b^3 x)/(y(y^2 −10b^2 ))) (2))) :} Remarque: ab=((3a^3 )/((x^2 −10a^2 )))×((3b^3 )/(y^2 −10b^2 )) =((9a^3 b^3 )/((x^2 −10a^2 )(y^2 −10b^2 ))) ⇒9a^2 b^2 =(x^2 −10a^2 )(y^2 −10b^2 ) cette equation nous permet de calculer a en fonction de b et y en fonxtion de x 9a^2 b^2 =x^2 y^2 −10b^2 x^2 −10a^2 y^2 +100a^2 b^2 91a^2 b^2 =10(a^2 y^2 +b^2 x^2 )−x^2 y^2 a^2 =((x^2 (10b^2 −y^2 ))/(91b^2 −10y^2 )) (si b≠y(√((10)/(91))) etb>(y/( (√(10)))))

$$\left(\mathrm{suite}\right) \\ $$$$ \\ $$$$\begin{cases}{\mathrm{bx}^{\mathrm{3}} −\mathrm{10ba}^{\mathrm{2}} \mathrm{x}=\mathrm{3a}^{\mathrm{3}} \mathrm{y}\:\:\:\Rightarrow\boldsymbol{\mathrm{b}}=\frac{\mathrm{3}\boldsymbol{\mathrm{a}}^{\mathrm{3}} \mathrm{y}}{\mathrm{x}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{10}\boldsymbol{\mathrm{a}}^{\mathrm{2}} \right)}\:\left(\mathrm{1}\right)}\\{\mathrm{ay}^{\mathrm{3}} −\mathrm{10ab}^{\mathrm{2}} \mathrm{y}=\mathrm{3b}^{\mathrm{3}} \mathrm{x}\:\:\Rightarrow\boldsymbol{\mathrm{a}}=\frac{\mathrm{3}\boldsymbol{\mathrm{b}}^{\mathrm{3}} \mathrm{x}}{\mathrm{y}\left(\mathrm{y}^{\mathrm{2}} −\mathrm{10b}^{\mathrm{2}} \right)}\:\:\left(\mathrm{2}\right)}\end{cases} \\ $$$$ \\ $$$$\boldsymbol{\mathrm{Remarque}}: \\ $$$$\mathrm{ab}=\frac{\mathrm{3a}^{\mathrm{3}} }{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{10a}^{\mathrm{2}} \right)}×\frac{\mathrm{3b}^{\mathrm{3}} }{\mathrm{y}^{\mathrm{2}} −\mathrm{10b}^{\mathrm{2}} } \\ $$$$\:\:\:\:=\frac{\mathrm{9a}^{\mathrm{3}} \mathrm{b}^{\mathrm{3}} }{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{10a}^{\mathrm{2}} \right)\left(\mathrm{y}^{\mathrm{2}} −\mathrm{10b}^{\mathrm{2}} \right)} \\ $$$$\Rightarrow\mathrm{9a}^{\mathrm{2}} \mathrm{b}^{\mathrm{2}} =\left(\mathrm{x}^{\mathrm{2}} −\mathrm{10a}^{\mathrm{2}} \right)\left(\mathrm{y}^{\mathrm{2}} −\mathrm{10b}^{\mathrm{2}} \right) \\ $$$$\mathrm{cette}\:\mathrm{equation}\:\mathrm{nous}\:\mathrm{permet}\:\:\mathrm{de}\:\mathrm{calculer} \\ $$$$\:\:\boldsymbol{\mathrm{a}}\:\mathrm{en}\:\mathrm{fonction}\:\:\mathrm{de}\:\boldsymbol{\mathrm{b}}\:\:\mathrm{et}\:\:\:\boldsymbol{\mathrm{y}}\:\mathrm{en}\:\mathrm{fonxtion}\:\mathrm{de}\:\boldsymbol{\mathrm{x}} \\ $$$$\mathrm{9}\boldsymbol{\mathrm{a}}^{\mathrm{2}} \boldsymbol{\mathrm{b}}^{\mathrm{2}} =\boldsymbol{\mathrm{x}}^{\mathrm{2}} \boldsymbol{\mathrm{y}}^{\mathrm{2}} −\mathrm{10}\boldsymbol{\mathrm{b}}^{\mathrm{2}} \boldsymbol{\mathrm{x}}^{\mathrm{2}} −\mathrm{10}\boldsymbol{\mathrm{a}}^{\mathrm{2}} \boldsymbol{\mathrm{y}}^{\mathrm{2}} +\mathrm{100}\boldsymbol{\mathrm{a}}^{\mathrm{2}} \boldsymbol{\mathrm{b}}^{\mathrm{2}} \\ $$$$\mathrm{91}\boldsymbol{\mathrm{a}}^{\mathrm{2}} \boldsymbol{\mathrm{b}}^{\mathrm{2}} =\mathrm{10}\left(\boldsymbol{\mathrm{a}}^{\mathrm{2}} \boldsymbol{\mathrm{y}}^{\mathrm{2}} +\boldsymbol{\mathrm{b}}^{\mathrm{2}} \boldsymbol{\mathrm{x}}^{\mathrm{2}} \right)−\boldsymbol{\mathrm{x}}^{\mathrm{2}} \boldsymbol{\mathrm{y}}^{\mathrm{2}} \\ $$$$ \\ $$$$\:\:\:\:\boldsymbol{\mathrm{a}}^{\mathrm{2}} =\frac{\boldsymbol{\mathrm{x}}^{\mathrm{2}} \left(\mathrm{10b}^{\mathrm{2}} −\boldsymbol{\mathrm{y}}^{\mathrm{2}} \right)}{\mathrm{91}\boldsymbol{\mathrm{b}}^{\mathrm{2}} −\mathrm{10}\boldsymbol{\mathrm{y}}^{\mathrm{2}} }\:\left(\boldsymbol{\mathrm{si}}\:\boldsymbol{\mathrm{b}}\neq\mathrm{y}\sqrt{\frac{\mathrm{10}}{\mathrm{91}}}\:\:\mathrm{etb}>\frac{\mathrm{y}}{\:\sqrt{\mathrm{10}}}\right)\: \\ $$$$ \\ $$

Answered by York12 last updated on 01/Jun/23

bx^3 = 10a^2 bx + 3a^3 y ........(i) ay^3 = 10ab^2 y + 3b^3 x .......(ii) (((i))/((ii))) we obtain : ((bx^3 )/(ay^3 ))=((a^2 (10bx + 3ay))/(b^2 (10ay + 3bx))) ⇒ ((b^3 x^3 )/(a^3 y^3 ))= ((10bx + 3ay)/(10ay +3bx)) = ((((10 bx)/(ay))+3)/(10 + ((3 bx)/(ay)))) set ((bx)/(ay)) = λ ⇒ λ^3 = ((10 λ +3)/(10 + 3 λ)) ⇒ 3λ^4 + 10 λ^(3 ) = 10λ +3 3λ^4 − 3 + 10 λ^3 −10 λ = 0 (λ^2 −1)(3λ^2 + 3) + 10 λ (λ^2 −1)=0 (λ−1)(λ+1)(λ+3)(3λ+1) =0 ⇒ λ ∈ { 1 , −1 , −3 , ((−1)/3) } By substituting we obtain The required values of x , y , a and b .★

$${bx}^{\mathrm{3}} \:=\:\mathrm{10}{a}^{\mathrm{2}} {bx}\:+\:\mathrm{3}{a}^{\mathrm{3}} {y}\:........\left({i}\right) \\ $$$${ay}^{\mathrm{3}} \:=\:\mathrm{10}{ab}^{\mathrm{2}} {y}\:+\:\mathrm{3}{b}^{\mathrm{3}} {x}\:\:.......\left({ii}\right) \\ $$$$\frac{\left({i}\right)}{\left({ii}\right)}\:{we}\:{obtain}\::\:\frac{{bx}^{\mathrm{3}} }{{ay}^{\mathrm{3}} }=\frac{{a}^{\mathrm{2}} \left(\mathrm{10}{bx}\:+\:\mathrm{3}{ay}\right)}{{b}^{\mathrm{2}} \left(\mathrm{10}{ay}\:+\:\mathrm{3}{bx}\right)}\: \\ $$$$\Rightarrow\:\frac{{b}^{\mathrm{3}} {x}^{\mathrm{3}} }{{a}^{\mathrm{3}} {y}^{\mathrm{3}} }=\:\frac{\mathrm{10}{bx}\:+\:\mathrm{3}{ay}}{\mathrm{10}{ay}\:+\mathrm{3}{bx}}\:=\:\frac{\frac{\mathrm{10}\:{bx}}{{ay}}+\mathrm{3}}{\mathrm{10}\:+\:\frac{\mathrm{3}\:{bx}}{{ay}}}\: \\ $$$${set}\:\frac{{bx}}{{ay}}\:=\:\lambda\:\Rightarrow\:\lambda^{\mathrm{3}} \:=\:\frac{\mathrm{10}\:\lambda\:+\mathrm{3}}{\mathrm{10}\:+\:\mathrm{3}\:\lambda}\:\Rightarrow\:\mathrm{3}\lambda^{\mathrm{4}} \:+\:\mathrm{10}\:\lambda^{\mathrm{3}\:} \:=\:\mathrm{10}\lambda\:+\mathrm{3}\: \\ $$$$\mathrm{3}\lambda^{\mathrm{4}} \:−\:\mathrm{3}\:+\:\mathrm{10}\:\lambda^{\mathrm{3}} \:−\mathrm{10}\:\lambda\:=\:\mathrm{0} \\ $$$$\left(\lambda^{\mathrm{2}} \:−\mathrm{1}\right)\left(\mathrm{3}\lambda^{\mathrm{2}} \:+\:\mathrm{3}\right)\:+\:\mathrm{10}\:\lambda\:\left(\lambda^{\mathrm{2}} \:−\mathrm{1}\right)=\mathrm{0} \\ $$$$\left(\lambda−\mathrm{1}\right)\left(\lambda+\mathrm{1}\right)\left(\lambda+\mathrm{3}\right)\left(\mathrm{3}\lambda+\mathrm{1}\right)\:=\mathrm{0}\: \\ $$$$\Rightarrow\:\lambda\:\in\:\left\{\:\mathrm{1}\:,\:−\mathrm{1}\:,\:−\mathrm{3}\:,\:\frac{−\mathrm{1}}{\mathrm{3}}\:\right\} \\ $$$${By}\:{substituting}\:{we}\:{obtain}\:{The}\:{required}\: \\ $$$${values}\:{of}\:{x}\:,\:{y}\:,\:{a}\:{and}\:{b}\:.\bigstar \\ $$$$ \\ $$

Commented by Frix last updated on 01/Jun/23

To divide 2 equations is not allowed: (1) 6=4 false (2) 3=2 false (((1))/((2))) (6/3)=(4/2) true

$$\mathrm{To}\:\mathrm{divide}\:\mathrm{2}\:\mathrm{equations}\:\mathrm{is}\:\mathrm{not}\:\mathrm{allowed}: \\ $$$$\left(\mathrm{1}\right)\:\mathrm{6}=\mathrm{4}\:\mathrm{false} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{3}=\mathrm{2}\:\mathrm{false} \\ $$$$\frac{\left(\mathrm{1}\right)}{\left(\mathrm{2}\right)}\:\frac{\mathrm{6}}{\mathrm{3}}=\frac{\mathrm{4}}{\mathrm{2}}\:\mathrm{true} \\ $$

Commented by ajfour last updated on 01/Jun/23

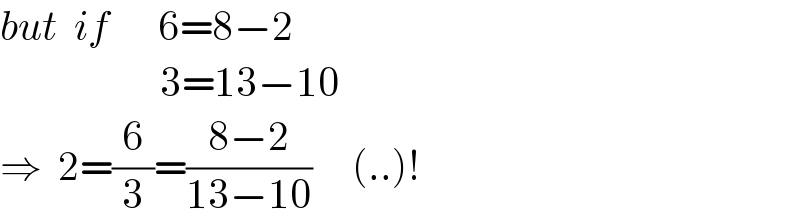
but if 6=8−2 3=13−10 ⇒ 2=(6/3)=((8−2)/(13−10)) (..)!

$${but}\:\:{if}\:\:\:\:\:\:\mathrm{6}=\mathrm{8}−\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{3}=\mathrm{13}−\mathrm{10} \\ $$$$\Rightarrow\:\:\mathrm{2}=\frac{\mathrm{6}}{\mathrm{3}}=\frac{\mathrm{8}−\mathrm{2}}{\mathrm{13}−\mathrm{10}}\:\:\:\:\:\left(..\right)! \\ $$

Commented by York12 last updated on 01/Jun/23

what you have written here is based on if 6=4 is false 3=2 is false but if the statement is true then we can always divide two equations

$${what}\:{you}\:{have}\:{written}\:{here}\:{is}\:{based}\:{on}\:{if}\: \\ $$$$\mathrm{6}=\mathrm{4}\:{is}\:{false}\: \\ $$$$\mathrm{3}=\mathrm{2}\:{is}\:{false}\: \\ $$$${but}\:{if}\:{the}\:{statement}\:{is}\:{true}\:{then}\:{we}\:{can}\:{always}\: \\ $$$${divide}\:{two}\:{equations}\: \\ $$

Commented by York12 last updated on 01/Jun/23

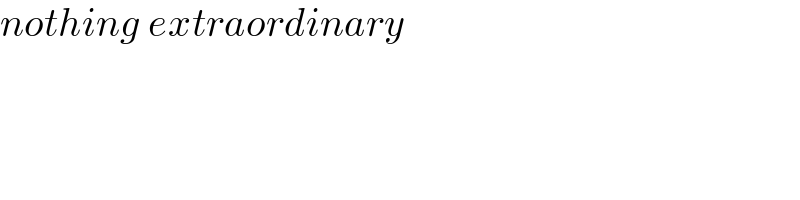
nothing extraordinary

$${nothing}\:{extraordinary} \\ $$

Commented by York12 last updated on 01/Jun/23

To divide 2 equations is not allowed: (1) 6=4 false (2) 3=2 false (((1))/((2))) (6/3)=(4/2) true whereas in my questions the equations are right then ((LHS_(equ (1)) )/(LHS_(equ(2)) )) =((RHS_(equ (1)) )/(RHS_(equ (2)) ))

$$ \\ $$$$\mathrm{To}\:\mathrm{divide}\:\mathrm{2}\:\mathrm{equations}\:\mathrm{is}\:\mathrm{not}\:\mathrm{allowed}: \\ $$$$\left(\mathrm{1}\right)\:\mathrm{6}=\mathrm{4}\:\mathrm{false} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{3}=\mathrm{2}\:\mathrm{false} \\ $$$$\frac{\left(\mathrm{1}\right)}{\left(\mathrm{2}\right)}\:\frac{\mathrm{6}}{\mathrm{3}}=\frac{\mathrm{4}}{\mathrm{2}}\:\mathrm{true} \\ $$$${whereas}\:{in}\:{my}\:{questions}\:{the}\:{equations}\: \\ $$$${are}\:{right}\:{then} \\ $$$$\frac{{LHS}_{{equ}\:\left(\mathrm{1}\right)} }{{LHS}_{{equ}\left(\mathrm{2}\right)} }\:=\frac{{RHS}_{{equ}\:\left(\mathrm{1}\right)} }{{RHS}_{{equ}\:\left(\mathrm{2}\right)} } \\ $$$$ \\ $$

Commented by Frix last updated on 01/Jun/23

You′re wrong here. Another example (we had some similar “solutions” here some time ago): (1) x^4 −x^3 −43x^2 +23x+203=0 (2) x^3 −6x^2 −13x+41=0 ================= (1) x^4 −x^3 −43x^2 −23x+210=7 (2) x^3 −6x^2 −13x+42=1 ================= (1) (x−7)(x−2)(x+3)(x+5)=7 (2) (x−7)(x−2)(x+3)=1 ================= (((1))/((2))) x+5=7 ⇒ x=2 (false) But both equations are “true”...

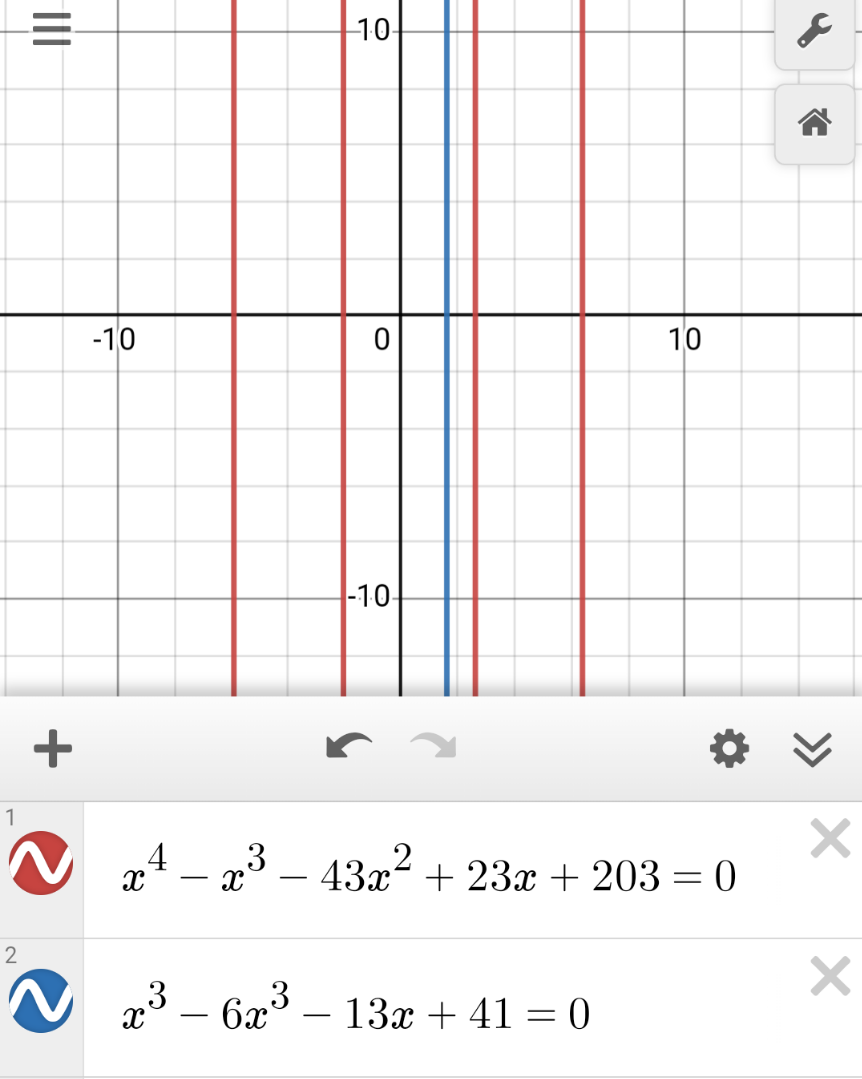
$$\mathrm{You}'\mathrm{re}\:\mathrm{wrong}\:\mathrm{here}. \\ $$$$\mathrm{Another}\:\mathrm{example}\:\left(\mathrm{we}\:\mathrm{had}\:\mathrm{some}\:\mathrm{similar}\right. \\ $$$$\left.``\mathrm{solutions}''\:\mathrm{here}\:\mathrm{some}\:\mathrm{time}\:\mathrm{ago}\right): \\ $$$$\left(\mathrm{1}\right)\:{x}^{\mathrm{4}} −{x}^{\mathrm{3}} −\mathrm{43}{x}^{\mathrm{2}} +\mathrm{23}{x}+\mathrm{203}=\mathrm{0} \\ $$$$\left(\mathrm{2}\right)\:{x}^{\mathrm{3}} −\mathrm{6}{x}^{\mathrm{2}} −\mathrm{13}{x}+\mathrm{41}=\mathrm{0} \\ $$$$================= \\ $$$$\left(\mathrm{1}\right)\:{x}^{\mathrm{4}} −{x}^{\mathrm{3}} −\mathrm{43}{x}^{\mathrm{2}} −\mathrm{23}{x}+\mathrm{210}=\mathrm{7} \\ $$$$\left(\mathrm{2}\right)\:{x}^{\mathrm{3}} −\mathrm{6}{x}^{\mathrm{2}} −\mathrm{13}{x}+\mathrm{42}=\mathrm{1} \\ $$$$================= \\ $$$$\left(\mathrm{1}\right)\:\left({x}−\mathrm{7}\right)\left({x}−\mathrm{2}\right)\left({x}+\mathrm{3}\right)\left({x}+\mathrm{5}\right)=\mathrm{7} \\ $$$$\left(\mathrm{2}\right)\:\left({x}−\mathrm{7}\right)\left({x}−\mathrm{2}\right)\left({x}+\mathrm{3}\right)=\mathrm{1} \\ $$$$================= \\ $$$$\frac{\left(\mathrm{1}\right)}{\left(\mathrm{2}\right)}\:{x}+\mathrm{5}=\mathrm{7}\:\Rightarrow\:{x}=\mathrm{2}\:\left(\mathrm{false}\right) \\ $$$$ \\ $$$$\mathrm{But}\:\mathrm{both}\:\mathrm{equations}\:\mathrm{are}\:``\mathrm{true}''... \\ $$

Commented by ajfour last updated on 02/Jun/23

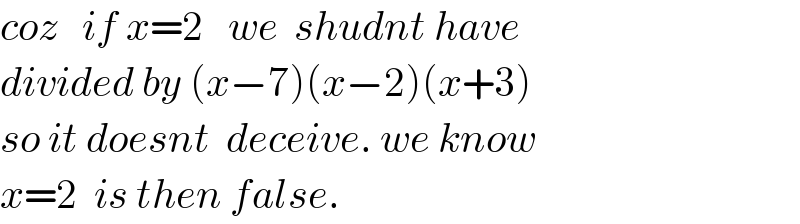
coz if x=2 we shudnt have divided by (x−7)(x−2)(x+3) so it doesnt deceive. we know x=2 is then false.

$${coz}\:\:\:{if}\:{x}=\mathrm{2}\:\:\:{we}\:\:{shudnt}\:{have} \\ $$$${divided}\:{by}\:\left({x}−\mathrm{7}\right)\left({x}−\mathrm{2}\right)\left({x}+\mathrm{3}\right) \\ $$$${so}\:{it}\:{doesnt}\:\:{deceive}.\:{we}\:{know} \\ $$$${x}=\mathrm{2}\:\:{is}\:{then}\:{false}. \\ $$

Commented by York12 last updated on 02/Jun/23

sorry but for again you are wrong because both equations canot be true simultaously (x−7)(x−2)(x+3)_(T) =1 (x−7)(x−2)(x+3)_(T) (x+5)=7 T =1 T × (x+5) =7 → x=2 That is so trivial but if you will substitute you will find that x doesnot satisfy the given system of equations then that means there are two variables to make that happen your equations has to written as (y−7)(y−2)(y+3)(x+5)=7 (y−7)(y−2)(y+3)=1 then that can happen and since you have commited such a mistake I advise you to study theory of equations specificly the concept of common roots cause those two equations that you have obtained doesnot have any common roots

$${sorry}\:{but}\:{for}\:{again}\:{you}\:{are}\:{wrong}\: \\ $$$${because}\:{both}\:{equations}\:{canot}\:{be}\:{true}\: \\ $$$${simultaously} \\ $$$$\underset{{T}} {\underbrace{\left({x}−\mathrm{7}\right)\left({x}−\mathrm{2}\right)\left({x}+\mathrm{3}\right)}}=\mathrm{1} \\ $$$$\underset{{T}} {\underbrace{\left({x}−\mathrm{7}\right)\left({x}−\mathrm{2}\right)\left({x}+\mathrm{3}\right)}}\left({x}+\mathrm{5}\right)=\mathrm{7} \\ $$$${T}\:=\mathrm{1}\: \\ $$$${T}\:×\:\left({x}+\mathrm{5}\right)\:=\mathrm{7}\:\rightarrow\:{x}=\mathrm{2} \\ $$$${That}\:{is}\:{so}\:{trivial}\: \\ $$$${but}\:{if}\:{you}\:{will}\:{substitute}\:{you}\:{will}\: \\ $$$${find}\:{that}\:{x}\:{doesnot}\:{satisfy}\:{the}\:{given} \\ $$$${system}\:{of}\:{equations} \\ $$$${then}\:{that}\:{means}\:{there}\:{are}\:{two}\:{variables} \\ $$$${to}\:{make}\:{that}\:{happen}\:{your}\:{equations} \\ $$$${has}\:{to}\:{written}\:{as}\: \\ $$$$\left({y}−\mathrm{7}\right)\left({y}−\mathrm{2}\right)\left({y}+\mathrm{3}\right)\left({x}+\mathrm{5}\right)=\mathrm{7} \\ $$$$\left({y}−\mathrm{7}\right)\left({y}−\mathrm{2}\right)\left({y}+\mathrm{3}\right)=\mathrm{1} \\ $$$${then}\:{that}\:{can}\:{happen}\:\: \\ $$$${and}\:{since}\:{you}\:{have}\:{commited} \\ $$$${such}\:{a}\:{mistake}\:{I}\:{advise}\:{you} \\ $$$${to}\:{study}\:{theory}\:{of}\:{equations} \\ $$$${specificly}\:{the}\:{concept}\:{of}\:{common}\:{roots} \\ $$$${cause}\:{those}\:{two}\:{equations}\:{that}\:{you}\:{have}\: \\ $$$${obtained}\:{doesnot}\:{have}\:{any}\:{common}\: \\ $$$${roots} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Commented by York12 last updated on 02/Jun/23

wrong cause both equtions can not be true cause they do not have any common roots !!!! then for again the assumptions are wrong

$${wrong} \\ $$$${cause}\:{both}\:{equtions}\:{can}\:{not}\:{be}\:{true}\: \\ $$$${cause}\:{they}\:{do}\:{not}\:{have}\:{any}\:{common}\:{roots}\:!!!! \\ $$$$ \\ $$$${then}\:{for}\:{again}\:{the}\:{assumptions} \\ $$$${are}\:{wrong}\: \\ $$$$ \\ $$

Commented by ajfour last updated on 02/Jun/23

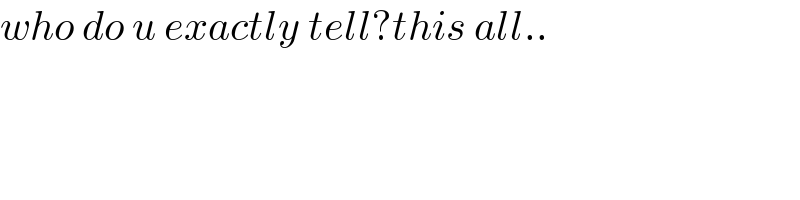
who do u exactly tell?this all..

$${who}\:{do}\:{u}\:{exactly}\:{tell}?{this}\:{all}.. \\ $$

Commented by York12 last updated on 02/Jun/23

to frix

$${to}\:{frix} \\ $$

Commented by ajfour last updated on 03/Jun/23

He's long past all this, we ll never get over!

Commented by Frix last updated on 08/Jun/23

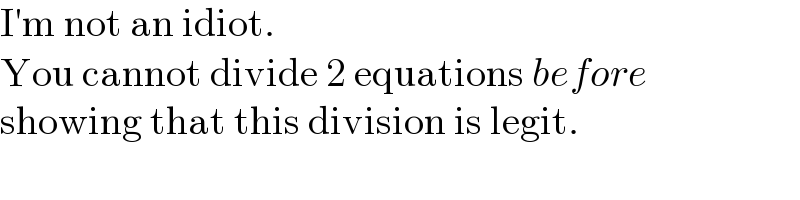
I′m not an idiot. You cannot divide 2 equations before showing that this division is legit.

$$\mathrm{I}'\mathrm{m}\:\mathrm{not}\:\mathrm{an}\:\mathrm{idiot}. \\ $$$$\mathrm{You}\:\mathrm{cannot}\:\mathrm{divide}\:\mathrm{2}\:\mathrm{equations}\:{before} \\ $$$$\mathrm{showing}\:\mathrm{that}\:\mathrm{this}\:\mathrm{division}\:\mathrm{is}\:\mathrm{legit}. \\ $$

Commented by York12 last updated on 13/Jun/23

no you can

$${no}\:{you}\:{can} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com