
Question Number 111195 by bemath last updated on 02/Sep/20
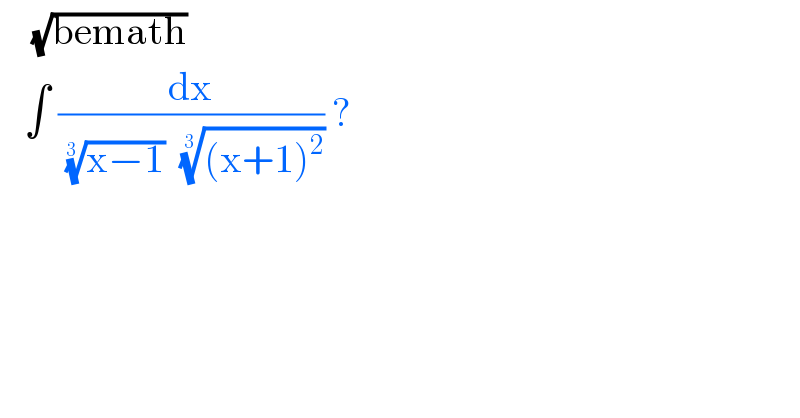
$$\:\:\:\:\sqrt{\mathrm{bemath}} \\ $$$$\:\:\:\int\:\frac{\mathrm{dx}}{\:\sqrt[{\mathrm{3}\:}]{\mathrm{x}−\mathrm{1}}\:\:\sqrt[{\mathrm{3}\:}]{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }}\:? \\ $$
Answered by Sarah85 last updated on 02/Sep/20

$$\mathrm{substitute}\:{t}=\sqrt[{\mathrm{3}}]{\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}}\:\Leftrightarrow\:{x}=−\frac{{t}^{\mathrm{3}} +\mathrm{1}}{{t}^{\mathrm{3}} −\mathrm{1}}\:\Rightarrow \\ $$$$\Rightarrow\:{dx}=\frac{\mathrm{3}}{\mathrm{2}}\sqrt[{\mathrm{3}}]{\left({x}−\mathrm{1}\right)^{\mathrm{2}} \left({x}+\mathrm{2}\right)^{\mathrm{4}} }{dt} \\ $$$$\Rightarrow \\ $$$$−\mathrm{3}\int\frac{{t}}{{t}^{\mathrm{3}} −\mathrm{1}}{dt}=−\int\frac{{dt}}{{t}−\mathrm{1}}+\int\frac{{t}−\mathrm{1}}{{t}^{\mathrm{2}} +{t}+\mathrm{1}}{dt}= \\ $$$$=−\mathrm{ln}\:\left({t}−\mathrm{1}\right)\:+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left({t}^{\mathrm{2}} +{t}+\mathrm{1}\right)\:−\sqrt{\mathrm{3}}\mathrm{arctan}\:\frac{\mathrm{2}{t}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\frac{{t}^{\mathrm{2}} +{t}+\mathrm{1}}{\left({t}−\mathrm{1}\right)^{\mathrm{2}} }\:−\sqrt{\mathrm{3}}\mathrm{arctan}\:\frac{\mathrm{2}{t}+\mathrm{1}}{\:\sqrt{\mathrm{3}}} \\ $$$$... \\ $$
Commented by bemath last updated on 03/Sep/20
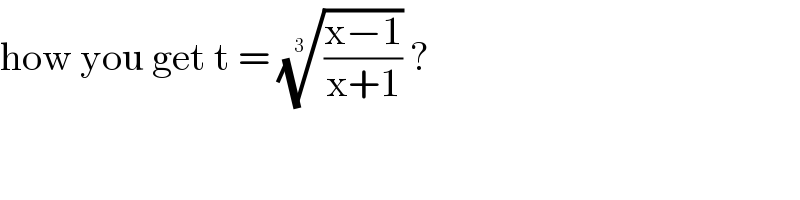
$$\mathrm{how}\:\mathrm{you}\:\mathrm{get}\:\mathrm{t}\:=\:\sqrt[{\mathrm{3}\:}]{\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}+\mathrm{1}}}\:? \\ $$
Commented by Sarah85 last updated on 03/Sep/20

$$\mathrm{try}\:\mathrm{and}\:\mathrm{error} \\ $$
Answered by mindispower last updated on 02/Sep/20
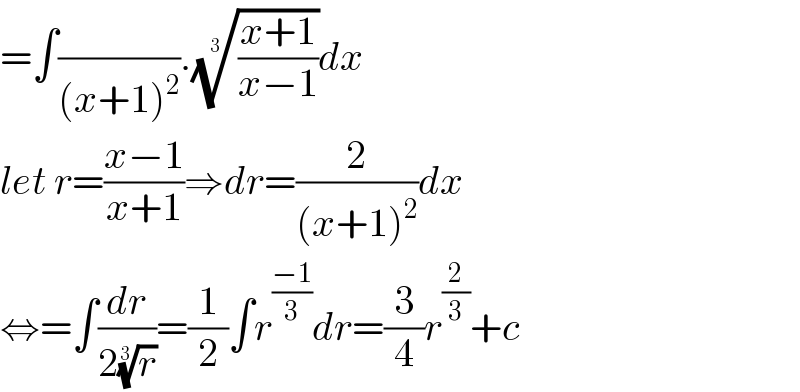
$$=\int\frac{}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }.\sqrt[{\mathrm{3}}]{\frac{{x}+\mathrm{1}}{{x}−\mathrm{1}}}{dx} \\ $$$${let}\:{r}=\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\Rightarrow{dr}=\frac{\mathrm{2}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }{dx} \\ $$$$\Leftrightarrow=\int\frac{{dr}}{\mathrm{2}\sqrt[{\mathrm{3}}]{{r}}}=\frac{\mathrm{1}}{\mathrm{2}}\int{r}^{\frac{−\mathrm{1}}{\mathrm{3}}} {dr}=\frac{\mathrm{3}}{\mathrm{4}}{r}^{\frac{\mathrm{2}}{\mathrm{3}}} +{c} \\ $$
Commented by Her_Majesty last updated on 02/Sep/20
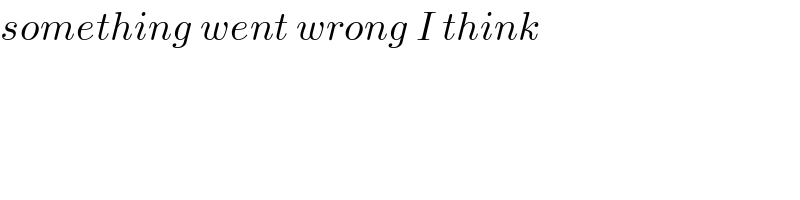
$${something}\:{went}\:{wrong}\:{I}\:{think} \\ $$
Commented by bobhans last updated on 03/Sep/20
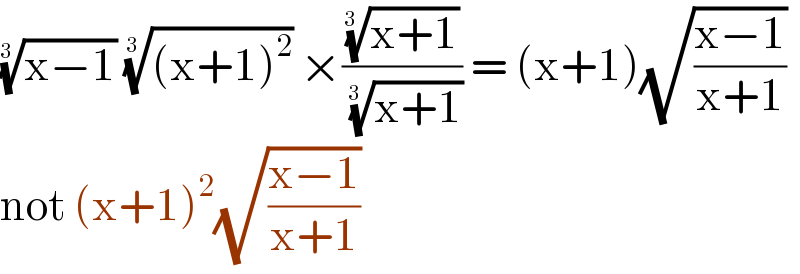
$$\sqrt[{\mathrm{3}\:}]{\mathrm{x}−\mathrm{1}}\:\sqrt[{\mathrm{3}\:}]{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\:×\frac{\sqrt[{\mathrm{3}\:}]{\mathrm{x}+\mathrm{1}}}{\:\sqrt[{\mathrm{3}\:}]{\mathrm{x}+\mathrm{1}}}\:=\:\left(\mathrm{x}+\mathrm{1}\right)\sqrt{\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}+\mathrm{1}}} \\ $$$$\mathrm{not}\:\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} \sqrt{\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}+\mathrm{1}}} \\ $$
