
Question Number 106958 by bemath last updated on 08/Aug/20
![@bemath@ (1) Given { ((x=sin α+sin β)),((y=cos α+cos β)) :} maximum value of x^2 +y^2 when α=... (2) find solution set the equation sin^4 x + sin^4 (x+(π/4))=(1/4) where x ∈ [0,2π]](Q106958.png)
$$\:\:\:@{bemath}@ \\ $$$$\left(\mathrm{1}\right)\:{Given}\:\begin{cases}{{x}=\mathrm{sin}\:\alpha+\mathrm{sin}\:\beta}\\{{y}=\mathrm{cos}\:\alpha+\mathrm{cos}\:\beta}\end{cases} \\ $$$${maximum}\:{value}\:{of}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \:{when}\:\alpha=... \\ $$$$\left(\mathrm{2}\right)\:{find}\:{solution}\:{set}\:{the}\:{equation} \\ $$$$\mathrm{sin}\:^{\mathrm{4}} {x}\:+\:\mathrm{sin}\:^{\mathrm{4}} \left({x}+\frac{\pi}{\mathrm{4}}\right)=\frac{\mathrm{1}}{\mathrm{4}}\:{where}\:{x}\:\in\:\left[\mathrm{0},\mathrm{2}\pi\right]\: \\ $$
Answered by mr W last updated on 08/Aug/20
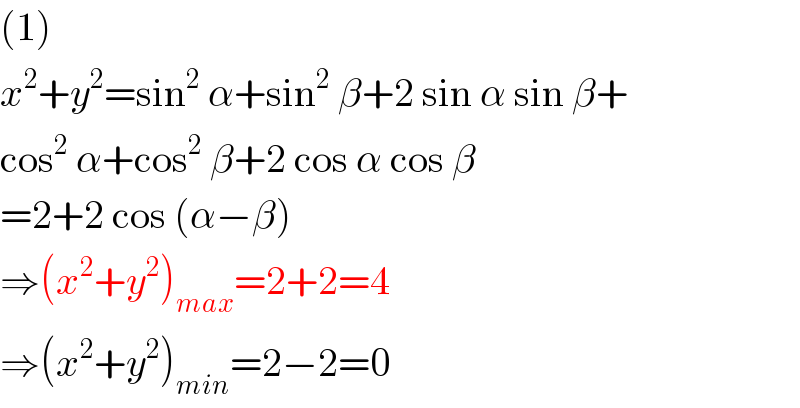
$$\left(\mathrm{1}\right) \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{sin}^{\mathrm{2}} \:\alpha+\mathrm{sin}^{\mathrm{2}} \:\beta+\mathrm{2}\:\mathrm{sin}\:\alpha\:\mathrm{sin}\:\beta+ \\ $$$$\mathrm{cos}^{\mathrm{2}} \:\alpha+\mathrm{cos}^{\mathrm{2}} \:\beta+\mathrm{2}\:\mathrm{cos}\:\alpha\:\mathrm{cos}\:\beta \\ $$$$=\mathrm{2}+\mathrm{2}\:\mathrm{cos}\:\left(\alpha−\beta\right) \\ $$$$\Rightarrow\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)_{{max}} =\mathrm{2}+\mathrm{2}=\mathrm{4} \\ $$$$\Rightarrow\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)_{{min}} =\mathrm{2}−\mathrm{2}=\mathrm{0} \\ $$
Commented by bemath last updated on 08/Aug/20

$${thank}\:{you}\:{mr}\:\mathcal{W} \\ $$
Commented by bemath last updated on 08/Aug/20
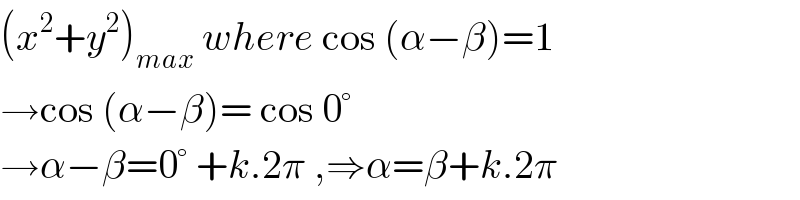
$$\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)_{{max}} \:{where}\:\mathrm{cos}\:\left(\alpha−\beta\right)=\mathrm{1} \\ $$$$\rightarrow\mathrm{cos}\:\left(\alpha−\beta\right)=\:\mathrm{cos}\:\mathrm{0}° \\ $$$$\rightarrow\alpha−\beta=\mathrm{0}°\:+{k}.\mathrm{2}\pi\:,\Rightarrow\alpha=\beta+{k}.\mathrm{2}\pi \\ $$
Answered by mr W last updated on 08/Aug/20
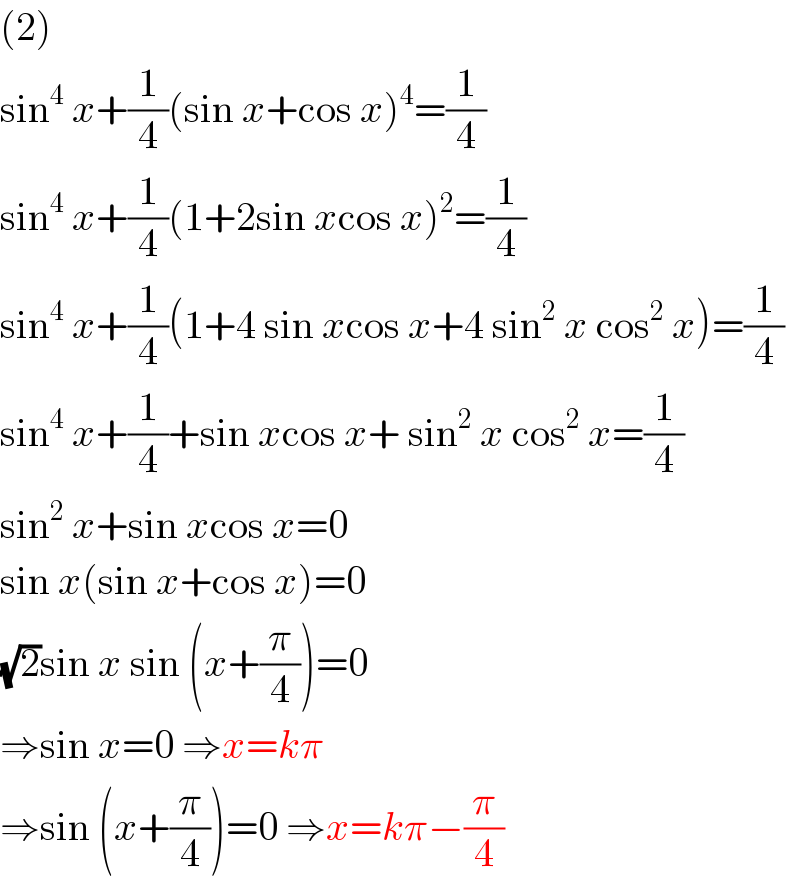
$$\left(\mathrm{2}\right) \\ $$$$\mathrm{sin}^{\mathrm{4}} \:{x}+\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{sin}\:{x}+\mathrm{cos}\:{x}\right)^{\mathrm{4}} =\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\mathrm{sin}^{\mathrm{4}} \:{x}+\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{1}+\mathrm{2sin}\:{x}\mathrm{cos}\:{x}\right)^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\mathrm{sin}^{\mathrm{4}} \:{x}+\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{1}+\mathrm{4}\:\mathrm{sin}\:{x}\mathrm{cos}\:{x}+\mathrm{4}\:\mathrm{sin}^{\mathrm{2}} \:{x}\:\mathrm{cos}^{\mathrm{2}} \:{x}\right)=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\mathrm{sin}^{\mathrm{4}} \:{x}+\frac{\mathrm{1}}{\mathrm{4}}+\mathrm{sin}\:{x}\mathrm{cos}\:{x}+\:\mathrm{sin}^{\mathrm{2}} \:{x}\:\mathrm{cos}^{\mathrm{2}} \:{x}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\mathrm{sin}^{\mathrm{2}} \:{x}+\mathrm{sin}\:{x}\mathrm{cos}\:{x}=\mathrm{0} \\ $$$$\mathrm{sin}\:{x}\left(\mathrm{sin}\:{x}+\mathrm{cos}\:{x}\right)=\mathrm{0} \\ $$$$\sqrt{\mathrm{2}}\mathrm{sin}\:{x}\:\mathrm{sin}\:\left({x}+\frac{\pi}{\mathrm{4}}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{sin}\:{x}=\mathrm{0}\:\Rightarrow{x}={k}\pi \\ $$$$\Rightarrow\mathrm{sin}\:\left({x}+\frac{\pi}{\mathrm{4}}\right)=\mathrm{0}\:\Rightarrow{x}={k}\pi−\frac{\pi}{\mathrm{4}} \\ $$
