Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 214568 by Ikbal last updated on 12/Dec/24

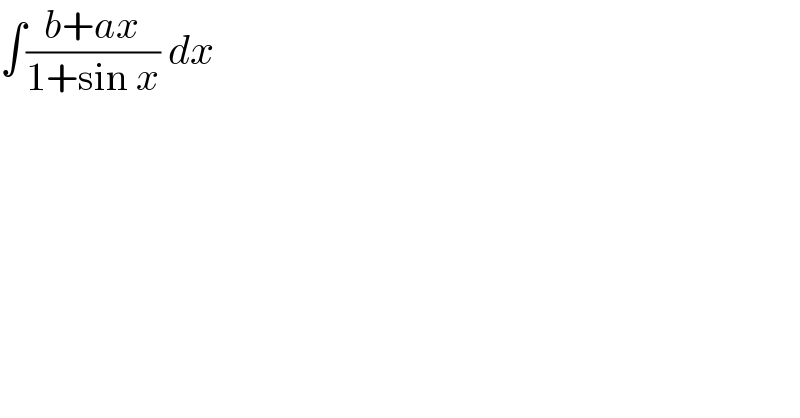
∫((b+ax)/(1+sin x)) dx

$$\int\frac{{b}+{ax}}{\mathrm{1}+\mathrm{sin}\:{x}}\:{dx} \\ $$

Answered by MathematicalUser2357 last updated on 18/Dec/24

∫((ax+b)/(sin x+1))dx =∫(((ax+b)sec x)/(tan x+sec x))dx =−((ax+b)/(tan x+sec x))+∫(a/(tan x+sec x))dx =−((ax+b)/(tan x+sec x))+a∫(1/(tan x+sec x))dx =−((ax+b)/(tan x+sec x))+a∫((sec x−tan x)/(sec^2 x−tan^2 x))dx =−((ax+b)/(tan x+sec x))+∫(sec x−tan x)dx =−((ax+b)/(tan x+sec x))+∫sec xdx−∫tan xdx =−((ax+b)/(tan x+sec x))+ln∣tan x+sec x∣dx−ln∣cos x∣+C

$$\int\frac{{ax}+{b}}{\mathrm{sin}\:{x}+\mathrm{1}}{dx} \\ $$$$=\int\frac{\left({ax}+{b}\right)\mathrm{sec}\:{x}}{\mathrm{tan}\:{x}+\mathrm{sec}\:{x}}{dx} \\ $$$$=−\frac{{ax}+{b}}{\mathrm{tan}\:{x}+\mathrm{sec}\:{x}}+\int\frac{{a}}{\mathrm{tan}\:{x}+\mathrm{sec}\:{x}}{dx} \\ $$$$=−\frac{{ax}+{b}}{\mathrm{tan}\:{x}+\mathrm{sec}\:{x}}+{a}\int\frac{\mathrm{1}}{\mathrm{tan}\:{x}+\mathrm{sec}\:{x}}{dx} \\ $$$$=−\frac{{ax}+{b}}{\mathrm{tan}\:{x}+\mathrm{sec}\:{x}}+{a}\int\frac{\mathrm{sec}\:{x}−\mathrm{tan}\:{x}}{\mathrm{sec}^{\mathrm{2}} {x}−\mathrm{tan}^{\mathrm{2}} {x}}{dx} \\ $$$$=−\frac{{ax}+{b}}{\mathrm{tan}\:{x}+\mathrm{sec}\:{x}}+\int\left(\mathrm{sec}\:{x}−\mathrm{tan}\:{x}\right){dx} \\ $$$$=−\frac{{ax}+{b}}{\mathrm{tan}\:{x}+\mathrm{sec}\:{x}}+\int\mathrm{sec}\:{xdx}−\int\mathrm{tan}\:{xdx} \\ $$$$=−\frac{{ax}+{b}}{\mathrm{tan}\:{x}+\mathrm{sec}\:{x}}+\mathrm{ln}\mid\mathrm{tan}\:{x}+\mathrm{sec}\:{x}\mid{dx}−\mathrm{ln}\mid\mathrm{cos}\:{x}\mid+{C} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com