
Question Number 52898 by MJS last updated on 14/Jan/19
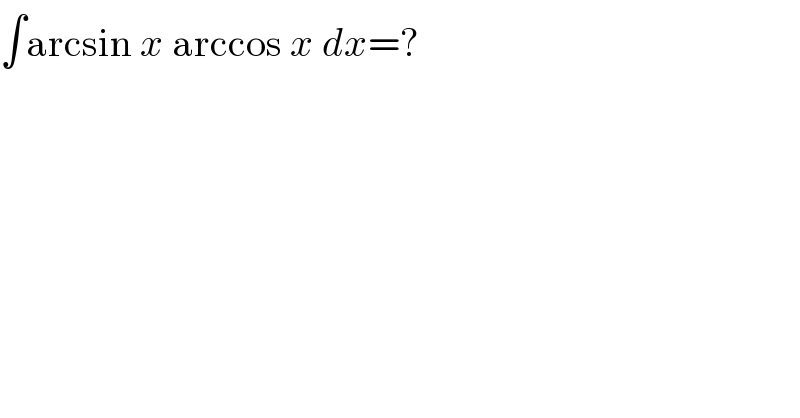
$$\int\mathrm{arcsin}\:{x}\:\mathrm{arccos}\:{x}\:{dx}=? \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 15/Jan/19
![a=sin^− x sina=x sin^(−1) x+cos^(−1) x=(π/2) ∫a×((π/2)−a)×cosada (π/2)∫acosada−∫a^2 cosada I=(π/2)I_1 −I_2 I_1 =∫acosada I_2 =∫a^2 cosada I_1 =a∫cosada−∫[(da/da)∫cosada]da =asina−∫sinada =asina+cosa+c_1 ←value of I_1 I_2 =∫a^2 cosada =a^2 sina−∫2asinada =a^2 sina−I_3 I_3 =∫2asinada =2a(−cosa)−∫2×−cosada =−2acosa+2sina so I_2 =a^2 sina+2acosa−2sina So I=(π/2)I_1 −I_2 =(π/2)(asina+cosa)−(a^2 sina+2acosa−2sina)+c =(π/2)(xsin^(−1) x+(√(1−x^2 )) )−[(sin^(−1) x)^2 x+2sin^(−1) x×(√(1−x^2 )) −2x)+c sir pls check...](Q52923.png)
$${a}={sin}^{−} {x} \\ $$$${sina}={x} \\ $$$${sin}^{−\mathrm{1}} {x}+{cos}^{−\mathrm{1}} {x}=\frac{\pi}{\mathrm{2}} \\ $$$$\int{a}×\left(\frac{\pi}{\mathrm{2}}−{a}\right)×{cosada} \\ $$$$\frac{\pi}{\mathrm{2}}\int{acosada}−\int{a}^{\mathrm{2}} {cosada} \\ $$$$\boldsymbol{{I}}=\frac{\pi}{\mathrm{2}}{I}_{\mathrm{1}} −\boldsymbol{{I}}_{\mathrm{2}} \\ $$$${I}_{\mathrm{1}} =\int{acosada}\:\:\:{I}_{\mathrm{2}} =\int{a}^{\mathrm{2}} {cosada} \\ $$$${I}_{\mathrm{1}} ={a}\int{cosada}−\int\left[\frac{{da}}{{da}}\int{cosada}\right]{da} \\ $$$$={asina}−\int{sinada} \\ $$$$={asina}+{cosa}+{c}_{\mathrm{1}} \:\:\leftarrow{value}\:{of}\:{I}_{\mathrm{1}} \\ $$$${I}_{\mathrm{2}} =\int{a}^{\mathrm{2}} {cosada} \\ $$$$={a}^{\mathrm{2}} {sina}−\int\mathrm{2}{asinada} \\ $$$$={a}^{\mathrm{2}} {sina}−{I}_{\mathrm{3}} \\ $$$${I}_{\mathrm{3}} =\int\mathrm{2}{asinada} \\ $$$$=\mathrm{2}{a}\left(−{cosa}\right)−\int\mathrm{2}×−{cosada} \\ $$$$=−\mathrm{2}{acosa}+\mathrm{2}{sina} \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{I}}_{\mathrm{2}} ={a}^{\mathrm{2}} {sina}+\mathrm{2}{acosa}−\mathrm{2}{sina} \\ $$$$\boldsymbol{{S}}{o}\:\boldsymbol{{I}}=\frac{\pi}{\mathrm{2}}\boldsymbol{{I}}_{\mathrm{1}} −\boldsymbol{{I}}_{\mathrm{2}} \\ $$$$=\frac{\pi}{\mathrm{2}}\left({asina}+{cosa}\right)−\left({a}^{\mathrm{2}} {sina}+\mathrm{2}{acosa}−\mathrm{2}{sina}\right)+{c} \\ $$$$=\frac{\pi}{\mathrm{2}}\left({xsin}^{−\mathrm{1}} {x}+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:\right)−\left[\left({sin}^{−\mathrm{1}} {x}\right)^{\mathrm{2}} {x}+\mathrm{2}{sin}^{−\mathrm{1}} {x}×\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:−\mathrm{2}{x}\right)+{c} \\ $$$${sir}\:{pls}\:{check}... \\ $$$$ \\ $$$$ \\ $$
