
Question Number 94285 by mathmax by abdo last updated on 17/May/20
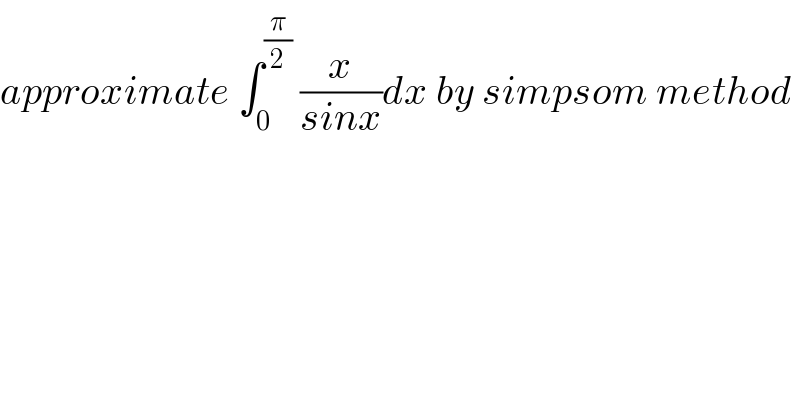
$${approximate}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{x}}{{sinx}}{dx}\:{by}\:{simpsom}\:{method} \\ $$
Commented by PRITHWISH SEN 2 last updated on 18/May/20
![taking 7 ordinates at x=0,(π/(12)),(π/6),(π/4),(π/3),((5π)/(12)),(π/2) here h=(1/6) x f(x)= (x/(sin x)) 0 ∽ 1 =y_0 (considering the limiting value) (π/(12)) 1.011515 = y_1 (π/6) 1.047197 = y_2 (π/4) 1.110720 = y_3 (π/3) 1.209199 = y_4 ((5π)/(12)) 1.355173 = y_5 (π/2) 1.570796 = y_6 applying Simpson′s one third rule I_(1/3) = (h/3)[(y_0 +y_6 )+4(y_1 +y_3 +y_5 )+2(y_2 +y_4 )] = (1/(18)){2.570796+13.909632+4.512792} = 1.16629 please check.](Q94411.png)
$$\mathrm{taking}\:\mathrm{7}\:\mathrm{ordinates}\:\mathrm{at}\:\boldsymbol{\mathrm{x}}=\mathrm{0},\frac{\pi}{\mathrm{12}},\frac{\pi}{\mathrm{6}},\frac{\pi}{\mathrm{4}},\frac{\pi}{\mathrm{3}},\frac{\mathrm{5}\pi}{\mathrm{12}},\frac{\pi}{\mathrm{2}} \\ $$$$\mathrm{here}\:\:\mathrm{h}=\frac{\mathrm{1}}{\mathrm{6}} \\ $$$$\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{x}}\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{f}}\left(\boldsymbol{\mathrm{x}}\right)=\:\frac{\boldsymbol{\mathrm{x}}}{\mathrm{sin}\:\boldsymbol{\mathrm{x}}} \\ $$$$\:\:\:\:\:\mathrm{0}\:\:\:\backsim\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:=\mathrm{y}_{\mathrm{0}} \:\:\:\left(\boldsymbol{\mathrm{considering}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{limiting}}\:\boldsymbol{\mathrm{value}}\right) \\ $$$$\:\:\:\:\:\frac{\pi}{\mathrm{12}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}.\mathrm{011515}\:=\:\mathrm{y}_{\mathrm{1}} \\ $$$$\:\:\:\:\:\frac{\pi}{\mathrm{6}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}.\mathrm{047197}\:=\:\mathrm{y}_{\mathrm{2}} \\ $$$$\:\:\:\:\:\frac{\pi}{\mathrm{4}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}.\mathrm{110720}\:=\:\mathrm{y}_{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\frac{\pi}{\mathrm{3}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}.\mathrm{209199}\:=\:\mathrm{y}_{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\frac{\mathrm{5}\pi}{\mathrm{12}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}.\mathrm{355173}\:=\:\mathrm{y}_{\mathrm{5}} \\ $$$$\:\:\:\:\:\:\:\frac{\pi}{\mathrm{2}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}.\mathrm{570796}\:=\:\mathrm{y}_{\mathrm{6}} \\ $$$$\mathrm{applying}\:\mathrm{Simpson}'\mathrm{s}\:\:\mathrm{one}\:\mathrm{third}\:\mathrm{rule} \\ $$$$\mathrm{I}_{\frac{\mathrm{1}}{\mathrm{3}}} \:\:\:\:=\:\frac{\mathrm{h}}{\mathrm{3}}\left[\left(\mathrm{y}_{\mathrm{0}} +\mathrm{y}_{\mathrm{6}} \right)+\mathrm{4}\left(\mathrm{y}_{\mathrm{1}} +\mathrm{y}_{\mathrm{3}} +\mathrm{y}_{\mathrm{5}} \right)+\mathrm{2}\left(\mathrm{y}_{\mathrm{2}} +\mathrm{y}_{\mathrm{4}} \right)\right]\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{1}}{\mathrm{18}}\left\{\mathrm{2}.\mathrm{570796}+\mathrm{13}.\mathrm{909632}+\mathrm{4}.\mathrm{512792}\right\} \\ $$$$\:\:\:\:\:\:\:\:\:=\:\mathrm{1}.\mathrm{16629}\:\:\boldsymbol{\mathrm{please}}\:\boldsymbol{\mathrm{check}}. \\ $$
Commented by mathmax by abdo last updated on 20/May/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by PRITHWISH SEN 2 last updated on 20/May/20

$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome} \\ $$
Answered by mathmax by abdo last updated on 20/May/20
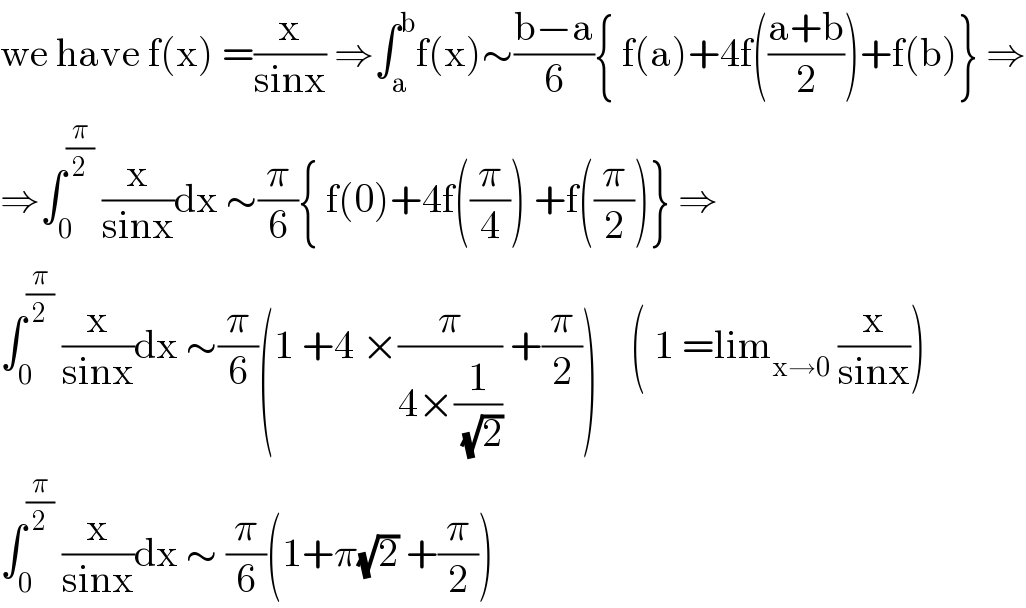
$$\mathrm{we}\:\mathrm{have}\:\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{x}}{\mathrm{sinx}}\:\Rightarrow\int_{\mathrm{a}} ^{\mathrm{b}} \mathrm{f}\left(\mathrm{x}\right)\sim\frac{\mathrm{b}−\mathrm{a}}{\mathrm{6}}\left\{\:\mathrm{f}\left(\mathrm{a}\right)+\mathrm{4f}\left(\frac{\mathrm{a}+\mathrm{b}}{\mathrm{2}}\right)+\mathrm{f}\left(\mathrm{b}\right)\right\}\:\Rightarrow \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{x}}{\mathrm{sinx}}\mathrm{dx}\:\sim\frac{\pi}{\mathrm{6}}\left\{\:\mathrm{f}\left(\mathrm{0}\right)+\mathrm{4f}\left(\frac{\pi}{\mathrm{4}}\right)\:+\mathrm{f}\left(\frac{\pi}{\mathrm{2}}\right)\right\}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{x}}{\mathrm{sinx}}\mathrm{dx}\:\sim\frac{\pi}{\mathrm{6}}\left(\mathrm{1}\:+\mathrm{4}\:×\frac{\pi}{\mathrm{4}×\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}}\:+\frac{\pi}{\mathrm{2}}\right)\:\:\:\:\left(\:\mathrm{1}\:=\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \:\frac{\mathrm{x}}{\mathrm{sinx}}\right) \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{x}}{\mathrm{sinx}}\mathrm{dx}\:\sim\:\frac{\pi}{\mathrm{6}}\left(\mathrm{1}+\pi\sqrt{\mathrm{2}}\:+\frac{\pi}{\mathrm{2}}\right) \\ $$
