Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 47364 by olj55336@awsoo.com last updated on 09/Nov/18

anybody please help q...∫cos^(−1) (√x) dx

$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$${anybody}\:{please}\:{help} \\ $$$${q}...\int\mathrm{cos}^{−\mathrm{1}} \sqrt{{x}}\:{dx} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Commented by maxmathsup by imad last updated on 09/Nov/18

changement (√x)=t give I =∫ arccos((√x))=∫2t arcos(t)dt =_(by parts) t^2 arcost +∫ t^2 (dt/(√(1−t^2 ))) but ∫ (t^2 /(√(1−t^2 )))dt = ∫ t .(t/(√(1−t^2 )))dt =_(by parts) −t (√(1−t^2 ))−∫ (√(1−t^2 ))dt and ∫ (√(1−t^2 ))dt =_(t=sinu) ∫ cosu cosu du =∫((1+co(2u))/2) =(u/2) +(1/4)sin(2u) =(u/2)+(1/2)sinu cosu =(1/2)arcsint +(1/2)t(√(1−t^2 )) ⇒ ∫ arcos((√x)) = xarcos((√x))−(√x)(√(1−x))−(1/2) arcsin((√x))−(1/2)(√x)(√(1−x)) +C =xarcos((√x))−(3/2)(√x)(√(1−x))−(1/2)arcsin((√x)) +C .

$${changement}\:\sqrt{{x}}={t}\:{give}\:{I}\:=\int\:{arccos}\left(\sqrt{{x}}\right)=\int\mathrm{2}{t}\:{arcos}\left({t}\right){dt}\:\: \\ $$$$=_{{by}\:{parts}} \:\:\:\:{t}^{\mathrm{2}} {arcost}\:+\int\:{t}^{\mathrm{2}} \:\:\frac{{dt}}{\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}\:{but} \\ $$$$\int\:\:\frac{{t}^{\mathrm{2}} }{\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}{dt}\:=\:\int\:{t}\:.\frac{{t}}{\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}{dt}\:=_{{by}\:{parts}} \:\:\:−{t}\:\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }−\int\:\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }{dt}\:{and} \\ $$$$\int\:\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }{dt}\:=_{{t}={sinu}} \:\:\int\:{cosu}\:{cosu}\:{du}\:=\int\frac{\mathrm{1}+{co}\left(\mathrm{2}{u}\right)}{\mathrm{2}} \\ $$$$=\frac{{u}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{4}}{sin}\left(\mathrm{2}{u}\right)\:=\frac{{u}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}{sinu}\:{cosu}\:=\frac{\mathrm{1}}{\mathrm{2}}{arcsint}\:\:+\frac{\mathrm{1}}{\mathrm{2}}{t}\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\int\:{arcos}\left(\sqrt{{x}}\right)\:=\:{xarcos}\left(\sqrt{{x}}\right)−\sqrt{{x}}\sqrt{\mathrm{1}−{x}}−\frac{\mathrm{1}}{\mathrm{2}}\:{arcsin}\left(\sqrt{{x}}\right)−\frac{\mathrm{1}}{\mathrm{2}}\sqrt{{x}}\sqrt{\mathrm{1}−{x}}\:+{C} \\ $$$$={xarcos}\left(\sqrt{{x}}\right)−\frac{\mathrm{3}}{\mathrm{2}}\sqrt{{x}}\sqrt{\mathrm{1}−{x}}−\frac{\mathrm{1}}{\mathrm{2}}{arcsin}\left(\sqrt{{x}}\right)\:+{C}\:. \\ $$

Answered by Smail last updated on 09/Nov/18

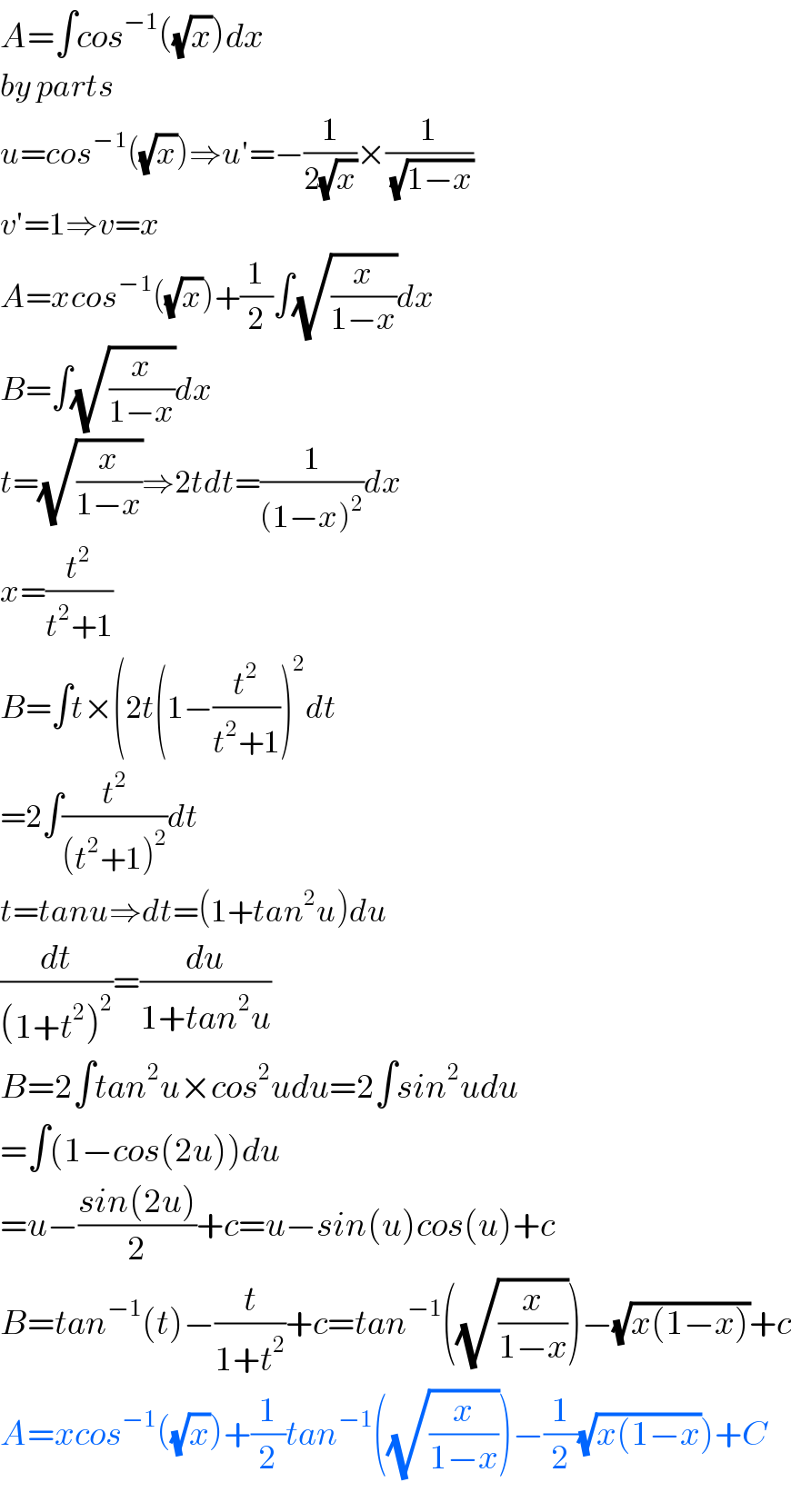
A=∫cos^(−1) ((√x))dx by parts u=cos^(−1) ((√x))⇒u′=−(1/(2(√x)))×(1/(√(1−x))) v′=1⇒v=x A=xcos^(−1) ((√x))+(1/2)∫(√(x/(1−x)))dx B=∫(√(x/(1−x)))dx t=(√(x/(1−x)))⇒2tdt=(1/((1−x)^2 ))dx x=(t^2 /(t^2 +1)) B=∫t×(2t(1−(t^2 /(t^2 +1)))^2 dt =2∫(t^2 /((t^2 +1)^2 ))dt t=tanu⇒dt=(1+tan^2 u)du (dt/((1+t^2 )^2 ))=(du/(1+tan^2 u)) B=2∫tan^2 u×cos^2 udu=2∫sin^2 udu =∫(1−cos(2u))du =u−((sin(2u))/2)+c=u−sin(u)cos(u)+c B=tan^(−1) (t)−(t/(1+t^2 ))+c=tan^(−1) ((√(x/(1−x))))−(√(x(1−x)))+c A=xcos^(−1) ((√x))+(1/2)tan^(−1) ((√(x/(1−x))))−(1/2)(√(x(1−x)))+C

$${A}=\int{cos}^{−\mathrm{1}} \left(\sqrt{{x}}\right){dx} \\ $$$${by}\:{parts} \\ $$$${u}={cos}^{−\mathrm{1}} \left(\sqrt{{x}}\right)\Rightarrow{u}'=−\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}}×\frac{\mathrm{1}}{\sqrt{\mathrm{1}−{x}}} \\ $$$${v}'=\mathrm{1}\Rightarrow{v}={x} \\ $$$${A}={xcos}^{−\mathrm{1}} \left(\sqrt{{x}}\right)+\frac{\mathrm{1}}{\mathrm{2}}\int\sqrt{\frac{{x}}{\mathrm{1}−{x}}}{dx} \\ $$$${B}=\int\sqrt{\frac{{x}}{\mathrm{1}−{x}}}{dx} \\ $$$${t}=\sqrt{\frac{{x}}{\mathrm{1}−{x}}}\Rightarrow\mathrm{2}{tdt}=\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }{dx} \\ $$$${x}=\frac{{t}^{\mathrm{2}} }{{t}^{\mathrm{2}} +\mathrm{1}} \\ $$$${B}=\int{t}×\left(\mathrm{2}{t}\left(\mathrm{1}−\frac{{t}^{\mathrm{2}} }{{t}^{\mathrm{2}} +\mathrm{1}}\right)^{\mathrm{2}} {dt}\right. \\ $$$$=\mathrm{2}\int\frac{{t}^{\mathrm{2}} }{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{dt} \\ $$$${t}={tanu}\Rightarrow{dt}=\left(\mathrm{1}+{tan}^{\mathrm{2}} {u}\right){du} \\ $$$$\frac{{dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }=\frac{{du}}{\mathrm{1}+{tan}^{\mathrm{2}} {u}} \\ $$$${B}=\mathrm{2}\int{tan}^{\mathrm{2}} {u}×{cos}^{\mathrm{2}} {udu}=\mathrm{2}\int{sin}^{\mathrm{2}} {udu} \\ $$$$=\int\left(\mathrm{1}−{cos}\left(\mathrm{2}{u}\right)\right){du} \\ $$$$={u}−\frac{{sin}\left(\mathrm{2}{u}\right)}{\mathrm{2}}+{c}={u}−{sin}\left({u}\right){cos}\left({u}\right)+{c} \\ $$$${B}={tan}^{−\mathrm{1}} \left({t}\right)−\frac{{t}}{\mathrm{1}+{t}^{\mathrm{2}} }+{c}={tan}^{−\mathrm{1}} \left(\sqrt{\frac{{x}}{\mathrm{1}−{x}}}\right)−\sqrt{{x}\left(\mathrm{1}−{x}\right)}+{c} \\ $$$$\left.{A}={xcos}^{−\mathrm{1}} \left(\sqrt{{x}}\right)+\frac{\mathrm{1}}{\mathrm{2}}{tan}^{−\mathrm{1}} \left(\sqrt{\frac{{x}}{\mathrm{1}−{x}}}\right)−\frac{\mathrm{1}}{\mathrm{2}}\sqrt{{x}\left(\mathrm{1}−{x}\right.}\right)+{C} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com