
Question Number 138723 by mnjuly1970 last updated on 17/Apr/21
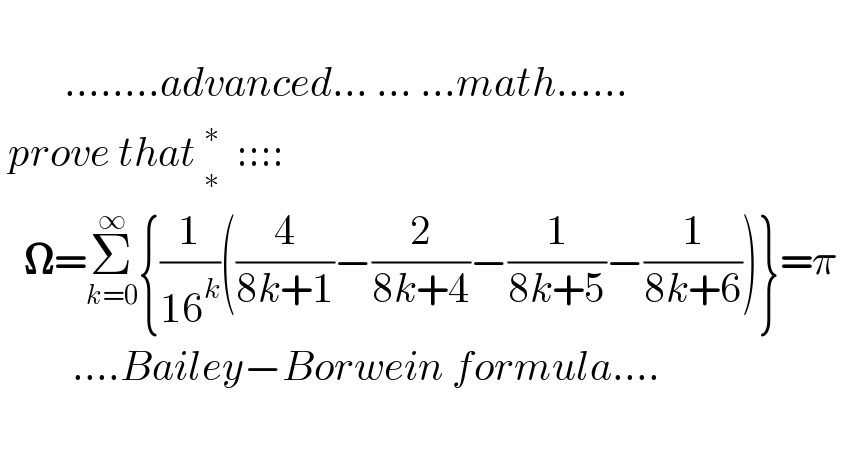
$$\:\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:........{advanced}...\:...\:...{math}...... \\ $$$$\:{prove}\:{that}\:_{\ast} ^{\ast} \:\::::: \\ $$$$\:\:\:\boldsymbol{\Omega}=\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\left\{\frac{\mathrm{1}}{\mathrm{16}^{{k}} }\left(\frac{\mathrm{4}}{\mathrm{8}{k}+\mathrm{1}}−\frac{\mathrm{2}}{\mathrm{8}{k}+\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{8}{k}+\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{8}{k}+\mathrm{6}}\right)\right\}=\pi \\ $$$$\:\:\:\:\:\:\:\:\:....{Bailey}−{Borwein}\:{formula}.... \\ $$$$\:\:\: \\ $$
Commented by Dwaipayan Shikari last updated on 17/Apr/21
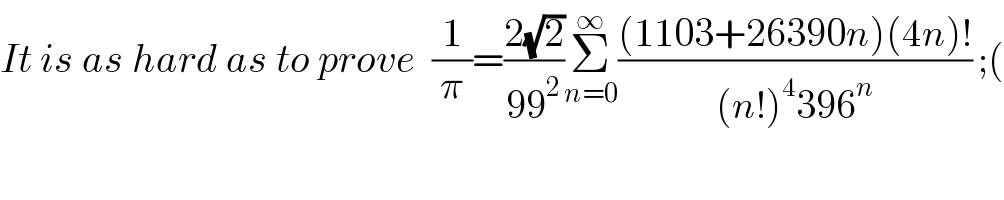
$${It}\:{is}\:{as}\:{hard}\:{as}\:{to}\:{prove}\:\:\frac{\mathrm{1}}{\pi}=\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{99}^{\mathrm{2}} }\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(\mathrm{1103}+\mathrm{26390}{n}\right)\left(\mathrm{4}{n}\right)!}{\left({n}!\right)^{\mathrm{4}} \mathrm{396}^{{n}} }\:;\left(\right. \\ $$
Commented by mnjuly1970 last updated on 17/Apr/21
$$\:{yes}\:{you}\:{are}\:{right}\:... \\ $$$$\:\: \\ $$
