Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 137048 by mnjuly1970 last updated on 29/Mar/21

........advanced ... ... ... calculus....... evaluate:::: π›˜=∫_0 ^( ∞) x^2 e^(βˆ’x^2 ) ln(x)=???

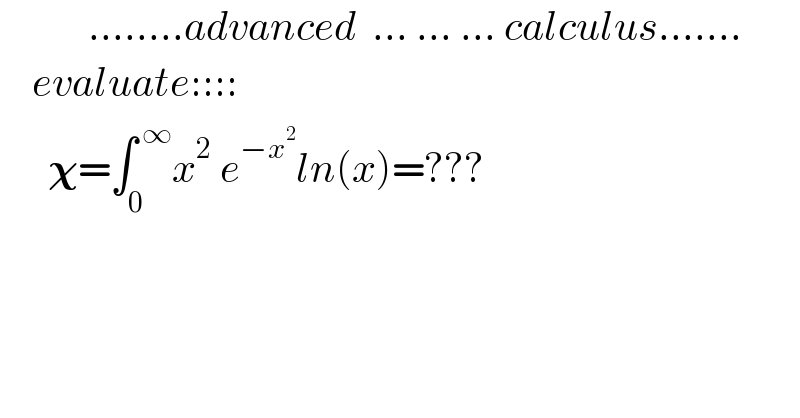
$$\:\:\:\:\:\:\:\:\:\:\:........{advanced}\:\:...\:...\:...\:{calculus}....... \\ $$$$\:\:\:\:{evaluate}:::: \\ $$$$\:\:\:\:\:\:\boldsymbol{\chi}=\int_{\mathrm{0}} ^{\:\infty} {x}^{\mathrm{2}} \:{e}^{βˆ’{x}^{\mathrm{2}} } {ln}\left({x}\right)=??? \\ $$$$\:\: \\ $$

Answered by Ar Brandon last updated on 29/Mar/21

π›˜=∫_0 ^∞ x^2 e^(βˆ’x^2 ) lnxdx=(βˆ‚/βˆ‚t)∣_(t=0) ∫_0 ^∞ x^(2+t) e^(βˆ’x^2 ) dx =^((u=x^2 )) (βˆ‚/βˆ‚t)∣_(t=0) (1/2)∫_0 ^∞ u^((1/2)+(t/2)) e^(βˆ’u) du=(βˆ‚/βˆ‚t)∣_(t=0) (1/2)Ξ“((3/2)+(t/2)) =(1/2)∣_(t=0) (1/2)Ξ“((3/2)+(t/2))ψ((3/2)+(t/2)) =(1/4)Ξ“((3/2))ψ((3/2))=(1/4)βˆ™((βˆšΟ€)/2)βˆ™(2βˆ’Ξ³βˆ’2ln2)

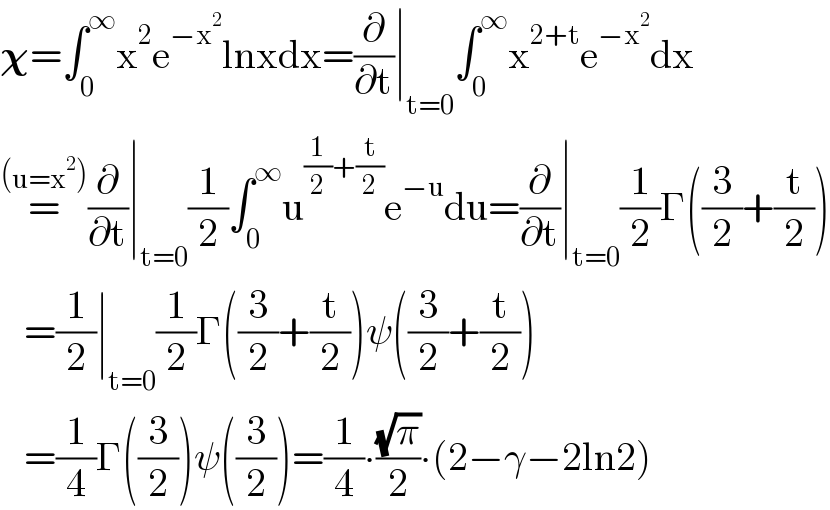
$$\boldsymbol{\chi}=\int_{\mathrm{0}} ^{\infty} \mathrm{x}^{\mathrm{2}} \mathrm{e}^{βˆ’\mathrm{x}^{\mathrm{2}} } \mathrm{lnxdx}=\frac{\partial}{\partial\mathrm{t}}\mid_{\mathrm{t}=\mathrm{0}} \int_{\mathrm{0}} ^{\infty} \mathrm{x}^{\mathrm{2}+\mathrm{t}} \mathrm{e}^{βˆ’\mathrm{x}^{\mathrm{2}} } \mathrm{dx} \\ $$$$\overset{\left(\mathrm{u}=\mathrm{x}^{\mathrm{2}} \right)} {=}\frac{\partial}{\partial\mathrm{t}}\mid_{\mathrm{t}=\mathrm{0}} \frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \mathrm{u}^{\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{t}}{\mathrm{2}}} \mathrm{e}^{βˆ’\mathrm{u}} \mathrm{du}=\frac{\partial}{\partial\mathrm{t}}\mid_{\mathrm{t}=\mathrm{0}} \frac{\mathrm{1}}{\mathrm{2}}\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}+\frac{\mathrm{t}}{\mathrm{2}}\right) \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\mid_{\mathrm{t}=\mathrm{0}} \frac{\mathrm{1}}{\mathrm{2}}\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}+\frac{\mathrm{t}}{\mathrm{2}}\right)\psi\left(\frac{\mathrm{3}}{\mathrm{2}}+\frac{\mathrm{t}}{\mathrm{2}}\right) \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{4}}\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)\psi\left(\frac{\mathrm{3}}{\mathrm{2}}\right)=\frac{\mathrm{1}}{\mathrm{4}}\centerdot\frac{\sqrt{\pi}}{\mathrm{2}}\centerdot\left(\mathrm{2}βˆ’\gammaβˆ’\mathrm{2ln2}\right) \\ $$

Commented by mnjuly1970 last updated on 29/Mar/21

very very nice mr brandon ..thank you...

$$\:{very}\:{very}\:{nice} \\ $$$$\:\:{mr}\:{brandon}\:..{thank}\:{you}... \\ $$

Commented by Ar Brandon last updated on 29/Mar/21

My pleasure, Sir

Answered by Dwaipayan Shikari last updated on 29/Mar/21

∫_0 ^∞ x^2 e^(βˆ’x^2 ) log(x)dx=β„΅β€²(3) β„΅(Ξ±)=∫_0 ^∞ x^(Ξ±βˆ’1) e^(βˆ’x^2 ) dxβ‡’β„΅(Ξ±)=(1/2)∫_0 ^∞ j^((Ξ±/2)βˆ’1) e^(βˆ’j) dj β„΅(Ξ±)=((Ξ“((Ξ±/2)))/2)β‡’β„΅β€²(Ξ±)=((Ξ“β€²((Ξ±/2)))/4)β‡’β„΅β€²(3)=((βˆšΟ€)/8)(βˆ’Ξ³+2βˆ’2log(2))

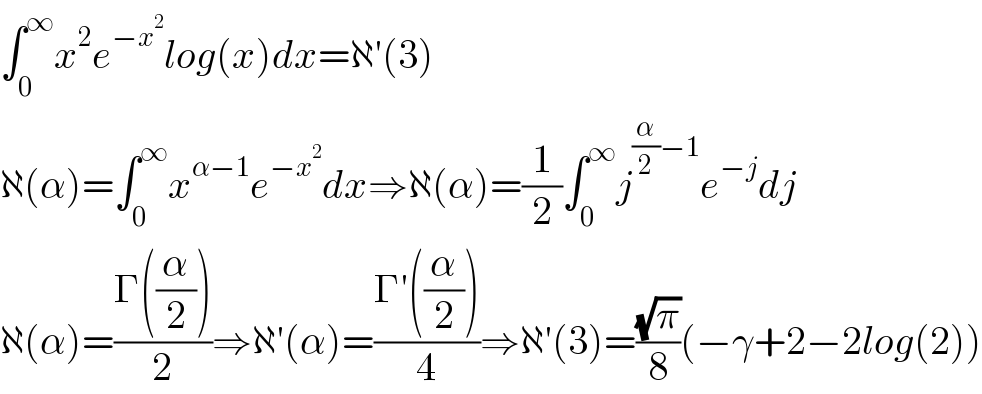
$$\int_{\mathrm{0}} ^{\infty} {x}^{\mathrm{2}} {e}^{βˆ’{x}^{\mathrm{2}} } {log}\left({x}\right){dx}=\aleph'\left(\mathrm{3}\right) \\ $$$$\aleph\left(\alpha\right)=\int_{\mathrm{0}} ^{\infty} {x}^{\alphaβˆ’\mathrm{1}} {e}^{βˆ’{x}^{\mathrm{2}} } {dx}\Rightarrow\aleph\left(\alpha\right)=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} {j}^{\frac{\alpha}{\mathrm{2}}βˆ’\mathrm{1}} {e}^{βˆ’{j}} {dj} \\ $$$$\aleph\left(\alpha\right)=\frac{\Gamma\left(\frac{\alpha}{\mathrm{2}}\right)}{\mathrm{2}}\Rightarrow\aleph'\left(\alpha\right)=\frac{\Gamma'\left(\frac{\alpha}{\mathrm{2}}\right)}{\mathrm{4}}\Rightarrow\aleph'\left(\mathrm{3}\right)=\frac{\sqrt{\pi}}{\mathrm{8}}\left(βˆ’\gamma+\mathrm{2}βˆ’\mathrm{2}{log}\left(\mathrm{2}\right)\right) \\ $$

Commented by mnjuly1970 last updated on 29/Mar/21

thanks alot mr payan...

$${thanks}\:{alot}\:{mr}\:{payan}... \\ $$

Commented by Dwaipayan Shikari last updated on 29/Mar/21

Have a great day sir!

Answered by mathmax by abdo last updated on 30/Mar/21

Ξ¦=∫_0 ^∞ x^2 e^(βˆ’x^2 ) lnx dx let f(a) =∫_0 ^∞ x^a e^(βˆ’x^2 ) dx v(o) x^a e^(βˆ’x^2 ) ∼x^a ∫_0 ^ΞΎ (dx/x^(βˆ’a) ) cv β‡”βˆ’a<1 β‡’a>βˆ’1 we have f(a)=∫_0 ^∞ e^(alogx) e^(βˆ’x^2 ) dx β‡’f^β€² (a)=∫_0 ^∞ x^a e^(βˆ’x^2 ) logx dx and f^β€² (2)=∫_0 ^∞ x^2 e^(βˆ’x^2 ) logx dx changement x^2 =t givef(a)=∫_0 ^∞ t^(a/2) e^(βˆ’t) (dt/(2(√t))) =(1/2)∫_0 ^∞ t^((aβˆ’1)/2) e^(βˆ’t) dt =(1/2)∫_0 ^∞ t^(((aβˆ’1)/2)+1βˆ’1) e^(βˆ’t) dt =(1/2)∫_0 ^∞ t^(((a+1)/2)βˆ’1) e^(βˆ’t) dt =(1/2)Ξ“(((a+1)/2)) β‡’f^β€² (a)=(1/4)Ξ“^β€² (((a+1)/2)) β‡’ f^β€² (2) =(1/4)Ξ“^β€² ((3/2)) =Ξ¦

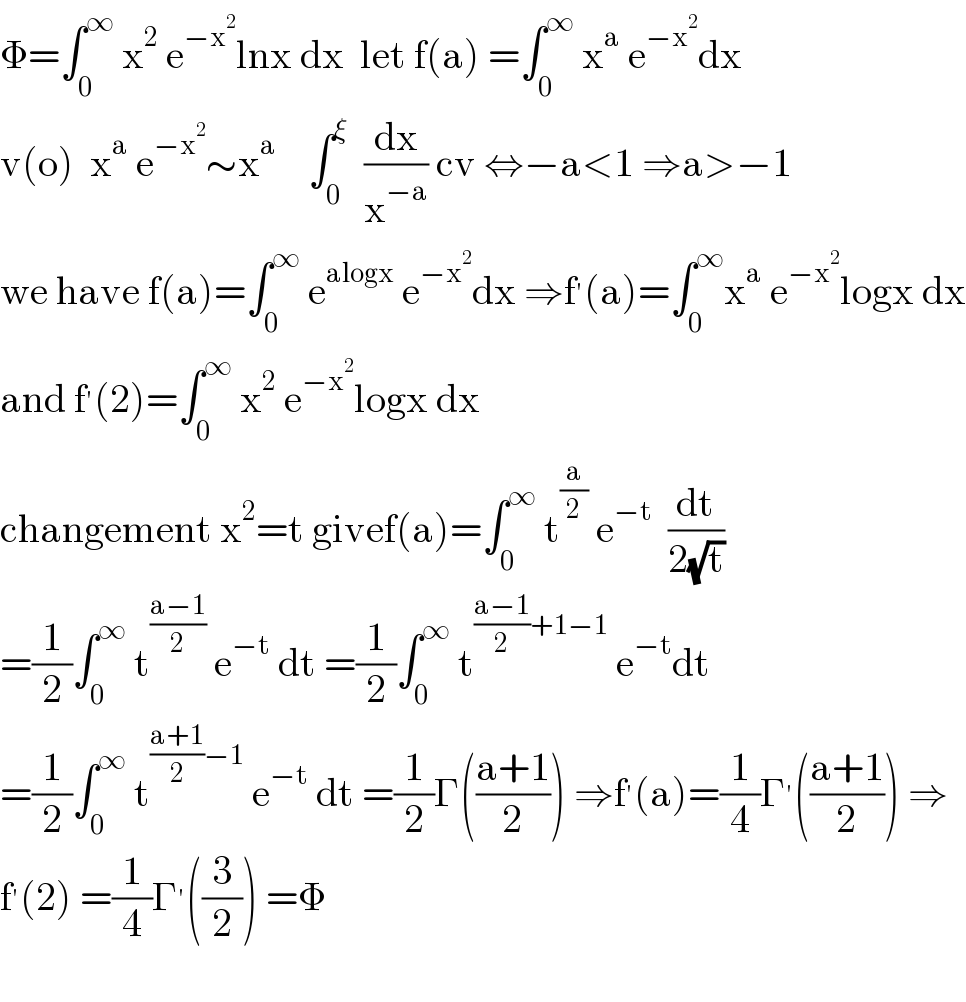
$$\Phi=\int_{\mathrm{0}} ^{\infty} \:\mathrm{x}^{\mathrm{2}} \:\mathrm{e}^{βˆ’\mathrm{x}^{\mathrm{2}} } \mathrm{lnx}\:\mathrm{dx}\:\:\mathrm{let}\:\mathrm{f}\left(\mathrm{a}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\mathrm{x}^{\mathrm{a}} \:\mathrm{e}^{βˆ’\mathrm{x}^{\mathrm{2}} } \mathrm{dx} \\ $$$$\mathrm{v}\left(\mathrm{o}\right)\:\:\mathrm{x}^{\mathrm{a}} \:\mathrm{e}^{βˆ’\mathrm{x}^{\mathrm{2}} } \sim\mathrm{x}^{\mathrm{a}} \:\:\:\:\int_{\mathrm{0}} ^{\xi} \:\:\frac{\mathrm{dx}}{\mathrm{x}^{βˆ’\mathrm{a}} }\:\mathrm{cv}\:\Leftrightarrowβˆ’\mathrm{a}<\mathrm{1}\:\Rightarrow\mathrm{a}>βˆ’\mathrm{1} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{f}\left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{\mathrm{alogx}} \:\mathrm{e}^{βˆ’\mathrm{x}^{\mathrm{2}} } \mathrm{dx}\:\Rightarrow\mathrm{f}^{'} \left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\infty} \mathrm{x}^{\mathrm{a}} \:\mathrm{e}^{βˆ’\mathrm{x}^{\mathrm{2}} } \mathrm{logx}\:\mathrm{dx} \\ $$$$\mathrm{and}\:\mathrm{f}^{'} \left(\mathrm{2}\right)=\int_{\mathrm{0}} ^{\infty} \:\mathrm{x}^{\mathrm{2}} \:\mathrm{e}^{βˆ’\mathrm{x}^{\mathrm{2}} } \mathrm{logx}\:\mathrm{dx} \\ $$$$\mathrm{changement}\:\mathrm{x}^{\mathrm{2}} =\mathrm{t}\:\mathrm{givef}\left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\infty} \:\mathrm{t}^{\frac{\mathrm{a}}{\mathrm{2}}} \:\mathrm{e}^{βˆ’\mathrm{t}} \:\:\frac{\mathrm{dt}}{\mathrm{2}\sqrt{\mathrm{t}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\mathrm{t}^{\frac{\mathrm{a}βˆ’\mathrm{1}}{\mathrm{2}}} \:\mathrm{e}^{βˆ’\mathrm{t}} \:\mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\mathrm{t}^{\frac{\mathrm{a}βˆ’\mathrm{1}}{\mathrm{2}}+\mathrm{1}βˆ’\mathrm{1}} \:\mathrm{e}^{βˆ’\mathrm{t}} \mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\mathrm{t}^{\frac{\mathrm{a}+\mathrm{1}}{\mathrm{2}}βˆ’\mathrm{1}} \:\mathrm{e}^{βˆ’\mathrm{t}} \:\mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{2}}\Gamma\left(\frac{\mathrm{a}+\mathrm{1}}{\mathrm{2}}\right)\:\Rightarrow\mathrm{f}^{'} \left(\mathrm{a}\right)=\frac{\mathrm{1}}{\mathrm{4}}\Gamma^{'} \left(\frac{\mathrm{a}+\mathrm{1}}{\mathrm{2}}\right)\:\Rightarrow \\ $$$$\mathrm{f}^{'} \left(\mathrm{2}\right)\:=\frac{\mathrm{1}}{\mathrm{4}}\Gamma^{'} \left(\frac{\mathrm{3}}{\mathrm{2}}\right)\:=\Phi \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com