Question and Answers Forum

All Questions      Topic List

Number Theory Questions

Previous in All Question      Next in All Question      

Previous in Number Theory      Next in Number Theory      

Question Number 202716 by Rasheed.Sindhi last updated on 01/Jan/24

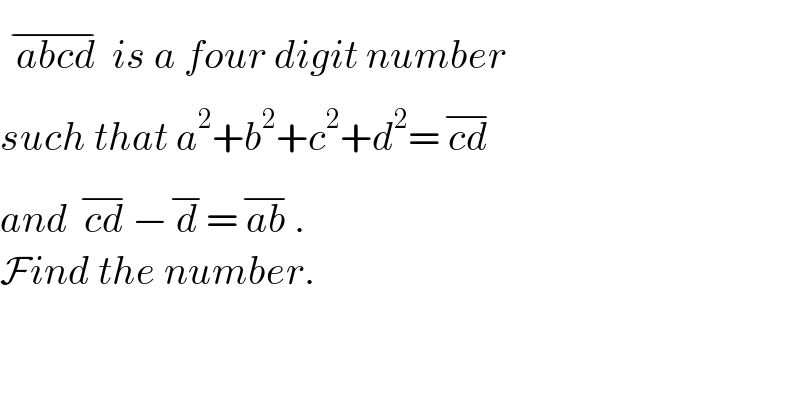
abcd ^(−) is a four digit number such that a^2 +b^2 +c^2 +d^2 = cd ^(−) and cd ^(−) − d ^(−) = ab ^(−) . Find the number.

$$\overline {\:\:{abcd}\:\:}{is}\:{a}\:{four}\:{digit}\:{number} \\ $$$${such}\:{that}\:{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +{d}^{\mathrm{2}} =\overline {\:{cd}\:} \\ $$$${and}\:\overline {\:{cd}\:}−\overline {\:{d}\:}=\overline {\:{ab}\:}. \\ $$$$\mathcal{F}{ind}\:{the}\:{number}. \\ $$

Answered by JDamian last updated on 01/Jan/24

cd^(__) − d^(_) = ab^(__) = c0^(__) ⇒ b=0 ∧ a=c a^2 +b^2 +c^2 +d^2 = cd^(__) =10c+d c^2 +0^2 +c^2 +d^2 = 10c+d 2c^2 +d^2 =10c+d d^2 −d = 10c−2c^2 d(d−1) = 2c(5−c) 2c(5−c)≥0 ⇒ c≤5 determinant ((c,(2c(5−c))),(0,0),(1,8),(2,(12)),(3,(12)),(4,8),(5,0)) determinant ((d,(d(d−1))),(1,0),(2,2),(3,6),(4,(12)),(5,(20)),(⋮,⋮)) d=4 ∧ c ∈ {2, 3} cd^(__) ∈ {24, 34} abcd^(____) ∈ {2024, 3034} Happy new year 2024... or 3034 if anybody reads this in 3034!!! lol

$$\overset{\_\_} {{cd}}\:−\:\overset{\_} {{d}}\:\:=\:\:\overset{\_\_} {{ab}}\:\:=\:\overset{\_\_} {{c}\mathrm{0}}\:\:\Rightarrow\:\:{b}=\mathrm{0}\:\:\:\wedge\:\:{a}={c} \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +{d}^{\mathrm{2}} =\:\overset{\_\_} {{cd}}\:=\mathrm{10}{c}+{d} \\ $$$${c}^{\mathrm{2}} +\mathrm{0}^{\mathrm{2}} +{c}^{\mathrm{2}} +{d}^{\mathrm{2}} =\:\mathrm{10}{c}+{d} \\ $$$$\mathrm{2}{c}^{\mathrm{2}} +{d}^{\mathrm{2}} =\mathrm{10}{c}+{d} \\ $$$${d}^{\mathrm{2}} −{d}\:=\:\mathrm{10}{c}−\mathrm{2}{c}^{\mathrm{2}} \\ $$$$\boldsymbol{{d}}\left(\boldsymbol{{d}}−\mathrm{1}\right)\:=\:\mathrm{2}\boldsymbol{{c}}\left(\mathrm{5}−\boldsymbol{{c}}\right) \\ $$$$\mathrm{2}{c}\left(\mathrm{5}−{c}\right)\geqslant\mathrm{0}\:\:\Rightarrow\:{c}\leqslant\mathrm{5} \\ $$$$ \\ $$$$\begin{array}{|c|c|c|c|c|c|c|}{{c}}&\hline{\mathrm{2}{c}\left(\mathrm{5}−{c}\right)}\\{\mathrm{0}}&\hline{\mathrm{0}}\\{\mathrm{1}}&\hline{\mathrm{8}}\\{\mathrm{2}}&\hline{\mathrm{12}}\\{\mathrm{3}}&\hline{\mathrm{12}}\\{\mathrm{4}}&\hline{\mathrm{8}}\\{\mathrm{5}}&\hline{\mathrm{0}}\\\hline\end{array}\:\:\:\:\begin{array}{|c|c|c|c|c|c|c|}{{d}}&\hline{{d}\left({d}−\mathrm{1}\right)}\\{\mathrm{1}}&\hline{\mathrm{0}}\\{\mathrm{2}}&\hline{\mathrm{2}}\\{\mathrm{3}}&\hline{\mathrm{6}}\\{\mathrm{4}}&\hline{\mathrm{12}}\\{\mathrm{5}}&\hline{\mathrm{20}}\\{\vdots}&\hline{\vdots}\\\hline\end{array} \\ $$$$ \\ $$$${d}=\mathrm{4}\:\:\wedge\:\:{c}\:\in\:\left\{\mathrm{2},\:\mathrm{3}\right\} \\ $$$$ \\ $$$$\overset{\_\_} {{cd}}\:\in\:\left\{\mathrm{24},\:\mathrm{34}\right\} \\ $$$$ \\ $$$$\overset{\_\_\_\_} {{abcd}}\:\in\:\left\{\mathrm{2024},\:\mathrm{3034}\right\} \\ $$$$ \\ $$$$\boldsymbol{{Happy}}\:\boldsymbol{{new}}\:\boldsymbol{{year}}\:\mathrm{2024}...\:{or}\:\mathrm{3034}\:{if} \\ $$$${anybody}\:{reads}\:{this}\:{in}\:\mathrm{3034}!!!\:\:{lol} \\ $$

Commented by Rasheed.Sindhi last updated on 01/Jan/24

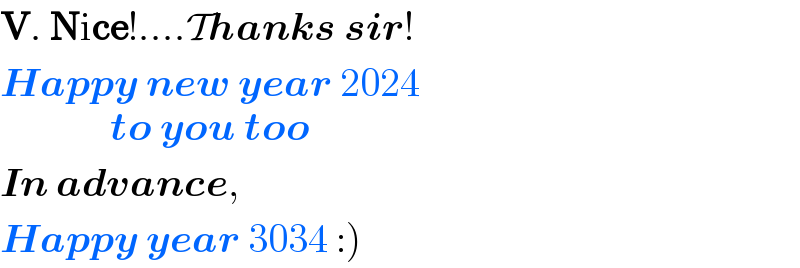
V. Nice!....Thanks sir! Happy new year 2024_(to you too) In advance, Happy year 3034 :)

$$\boldsymbol{\mathrm{V}}.\:\boldsymbol{\mathrm{N}}\mathrm{i}\boldsymbol{\mathrm{ce}}!....\mathcal{T}\boldsymbol{{hanks}}\:\boldsymbol{{sir}}! \\ $$$$\underset{\boldsymbol{{to}}\:\boldsymbol{{you}}\:\boldsymbol{{too}}} {\boldsymbol{{Happy}}\:\boldsymbol{{new}}\:\boldsymbol{{year}}\:\mathrm{2024}}\: \\ $$$$\boldsymbol{{In}}\:\boldsymbol{{advance}},\: \\ $$$$\left.\boldsymbol{{Happy}}\:\boldsymbol{{year}}\:\mathrm{3034}\::\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com