
Question Number 159966 by malwaan last updated on 23/Nov/21
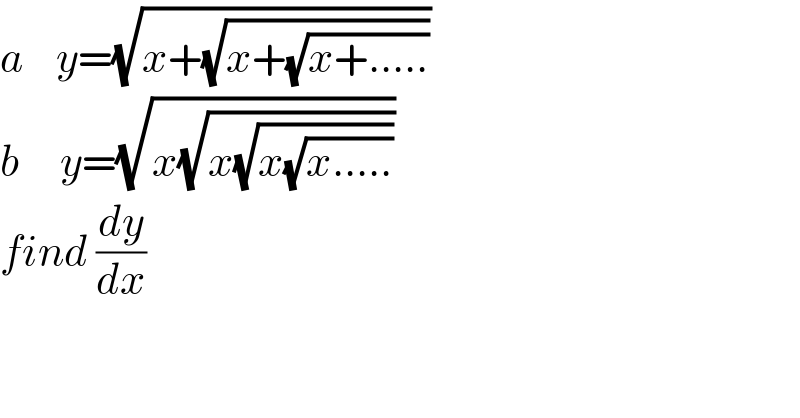
$${a}\:\:\:\:{y}=\sqrt{{x}+\sqrt{{x}+\sqrt{{x}+.....}}} \\ $$$${b}\:\:\:\:\:{y}=\sqrt{{x}\sqrt{{x}\sqrt{{x}\sqrt{{x}.....}}}} \\ $$$${find}\:\frac{{dy}}{{dx}} \\ $$
Commented by tounghoungko last updated on 23/Nov/21
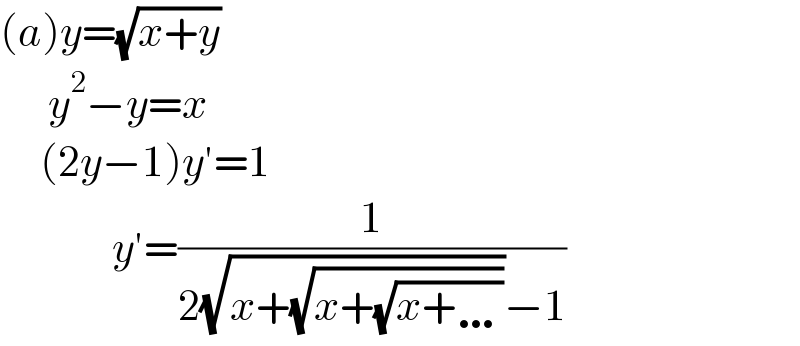
$$\left({a}\right){y}=\sqrt{{x}+{y}} \\ $$$$\:\:\:\:\:\:{y}^{\mathrm{2}} −{y}={x} \\ $$$$\:\:\:\:\:\left(\mathrm{2}{y}−\mathrm{1}\right){y}'=\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:{y}'=\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}+\sqrt{{x}+\sqrt{{x}+\ldots}}}−\mathrm{1}} \\ $$
Commented by mr W last updated on 23/Nov/21
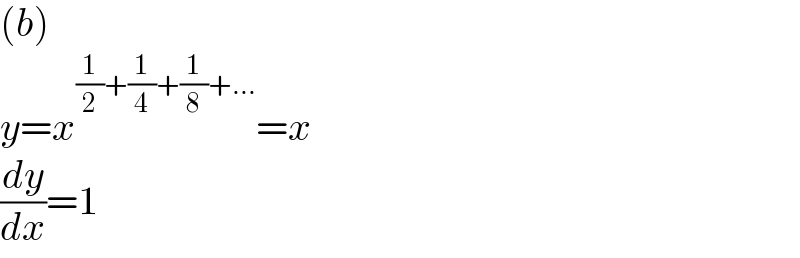
$$\left({b}\right) \\ $$$${y}={x}^{\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{8}}+...} ={x} \\ $$$$\frac{{dy}}{{dx}}=\mathrm{1} \\ $$
