
Question Number 217211 by Ghisom last updated on 06/Mar/25
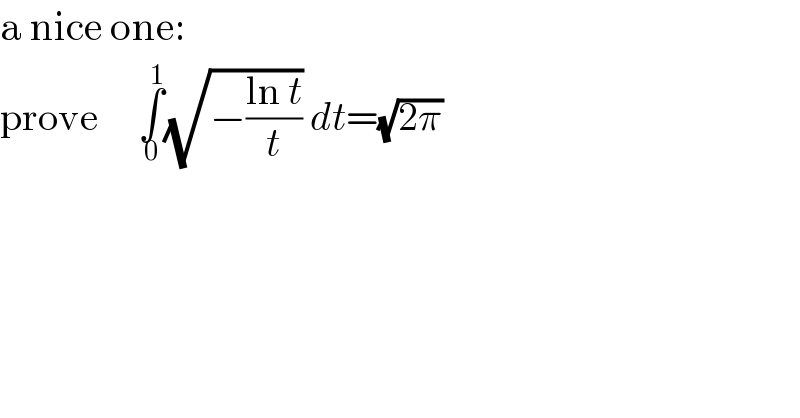
$$\mathrm{a}\:\mathrm{nice}\:\mathrm{one}: \\ $$$$\mathrm{prove}\:\:\:\:\:\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\sqrt{−\frac{\mathrm{ln}\:{t}}{{t}}}\:{dt}=\sqrt{\mathrm{2}\pi} \\ $$
Answered by MrGaster last updated on 06/Mar/25
![(1):∫_0 ^1 (√(−((ln t)/t)))dt=∫_0 ^1 t^(−(1/2)) (−ln t)^(1/2) dt =∫_0 ^∞ e^(−u) u^(−(1/2)) ((u/2))^(1/2) (du/u) (let t=e^(−u) ) =(1/( (√2)))∫_0 ^∞ e^(−u) u^((1/2)−1) du =(1/( (√2)))Γ((1/2)) =(1/( (√2)))(√π) =(√(π/2)) (√(π/2))=((√π)/( (√2))) =(√(2π)) (2)Let u=(√(−ln t))⇒t=e^(−u^2 ) ⇒dt=−2ue^(−u^2 ) du ∫_0 ^1 (√(−((ln t)/t)))dt=∫_0 ^∞ (√u^2 )∙(−2ue^(−u^2 ) )du=2∫_0 ^∞ u^2 e^(−u^2 ) du ∫_0 ^∞ e^(−u^2 ) du=((√π)/2) ∫_0 ^∞ u^2 e^(−u^2 ) du=(1/2)∫_0 ^∞ u∙(2ue^(−u^2 ) )du=(1/2)[−e^(−u^2 ) ]_0 ^∞ =(1/2) ⇒2∫_0 ^∞ u^2 e^(−u^2 ) du2∙(1/2)=1 ∴∫_0 ^1 (√(−((ln t)/t)))dt=(√(2π))](Q217213.png)
$$\left(\mathrm{1}\right):\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{−\frac{\mathrm{ln}\:{t}}{{t}}}{dt}=\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{−\frac{\mathrm{1}}{\mathrm{2}}} \left(−\mathrm{ln}\:{t}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} {dt} \\ $$$$=\int_{\mathrm{0}} ^{\infty} {e}^{−{u}} {u}^{−\frac{\mathrm{1}}{\mathrm{2}}} \left(\frac{{u}}{\mathrm{2}}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \frac{{du}}{{u}}\:\left(\mathrm{let}\:{t}={e}^{−{u}} \right) \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\int_{\mathrm{0}} ^{\infty} {e}^{−{u}} {u}^{\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}} {du} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\sqrt{\pi} \\ $$$$=\sqrt{\frac{\pi}{\mathrm{2}}} \\ $$$$\sqrt{\frac{\pi}{\mathrm{2}}}=\frac{\sqrt{\pi}}{\:\sqrt{\mathrm{2}}} =\sqrt{\mathrm{2}\pi} \\ $$$$\left(\mathrm{2}\right)\mathrm{Let}\:{u}=\sqrt{−\mathrm{ln}\:{t}}\Rightarrow{t}={e}^{−{u}^{\mathrm{2}} } \Rightarrow{dt}=−\mathrm{2}{ue}^{−{u}^{\mathrm{2}} } {du} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{−\frac{\mathrm{ln}\:{t}}{{t}}}{dt}=\int_{\mathrm{0}} ^{\infty} \sqrt{{u}^{\mathrm{2}} }\centerdot\left(−\mathrm{2}{ue}^{−{u}^{\mathrm{2}} } \right){du}=\mathrm{2}\int_{\mathrm{0}} ^{\infty} {u}^{\mathrm{2}} {e}^{−{u}^{\mathrm{2}} } {du} \\ $$$$\int_{\mathrm{0}} ^{\infty} {e}^{−{u}^{\mathrm{2}} } {du}=\frac{\sqrt{\pi}}{\mathrm{2}} \\ $$$$\int_{\mathrm{0}} ^{\infty} {u}^{\mathrm{2}} {e}^{−{u}^{\mathrm{2}} } {du}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} {u}\centerdot\left(\mathrm{2}{ue}^{−{u}^{\mathrm{2}} } \right){du}=\frac{\mathrm{1}}{\mathrm{2}}\left[−{e}^{−{u}^{\mathrm{2}} } \right]_{\mathrm{0}} ^{\infty} =\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{2}\int_{\mathrm{0}} ^{\infty} {u}^{\mathrm{2}} {e}^{−{u}^{\mathrm{2}} } {du}\mathrm{2}\centerdot\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{1} \\ $$$$\therefore\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{−\frac{\mathrm{ln}\:{t}}{{t}}}{dt}=\sqrt{\mathrm{2}\pi} \\ $$
Commented by Ghisom last updated on 06/Mar/25
��
