
Question Number 214216 by MathematicalUser2357 last updated on 01/Dec/24
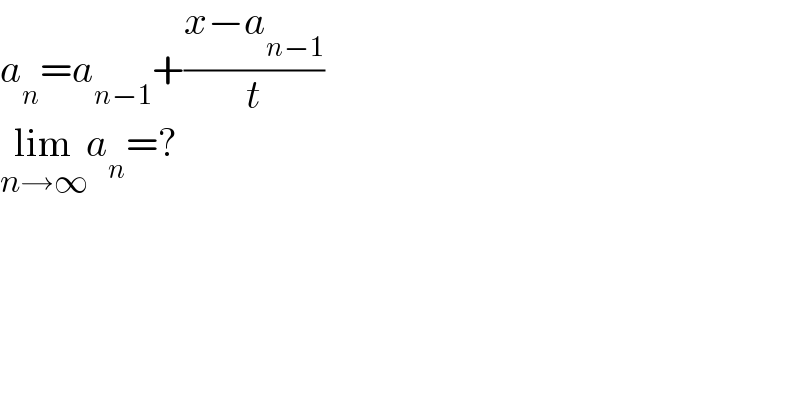
$${a}_{{n}} ={a}_{{n}−\mathrm{1}} +\frac{{x}−{a}_{{n}−\mathrm{1}} }{{t}} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}{a}_{{n}} =? \\ $$
Answered by mr W last updated on 01/Dec/24
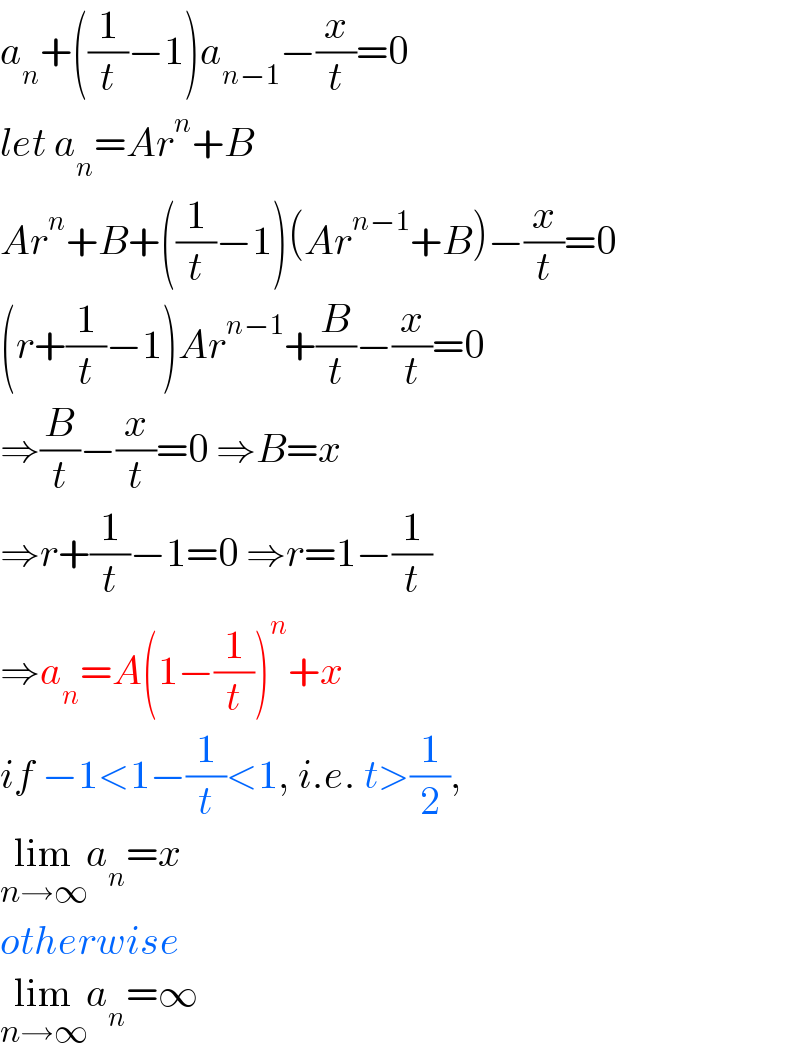
$${a}_{{n}} +\left(\frac{\mathrm{1}}{{t}}−\mathrm{1}\right){a}_{{n}−\mathrm{1}} −\frac{{x}}{{t}}=\mathrm{0} \\ $$$${let}\:{a}_{{n}} ={Ar}^{{n}} +{B} \\ $$$${Ar}^{{n}} +{B}+\left(\frac{\mathrm{1}}{{t}}−\mathrm{1}\right)\left({Ar}^{{n}−\mathrm{1}} +{B}\right)−\frac{{x}}{{t}}=\mathrm{0} \\ $$$$\left({r}+\frac{\mathrm{1}}{{t}}−\mathrm{1}\right){Ar}^{{n}−\mathrm{1}} +\frac{{B}}{{t}}−\frac{{x}}{{t}}=\mathrm{0} \\ $$$$\Rightarrow\frac{{B}}{{t}}−\frac{{x}}{{t}}=\mathrm{0}\:\Rightarrow{B}={x} \\ $$$$\Rightarrow{r}+\frac{\mathrm{1}}{{t}}−\mathrm{1}=\mathrm{0}\:\Rightarrow{r}=\mathrm{1}−\frac{\mathrm{1}}{{t}} \\ $$$$\Rightarrow{a}_{{n}} ={A}\left(\mathrm{1}−\frac{\mathrm{1}}{{t}}\right)^{{n}} +{x} \\ $$$${if}\:−\mathrm{1}<\mathrm{1}−\frac{\mathrm{1}}{{t}}<\mathrm{1},\:{i}.{e}.\:{t}>\frac{\mathrm{1}}{\mathrm{2}},\: \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}{a}_{{n}} ={x} \\ $$$${otherwise} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}{a}_{{n}} =\infty \\ $$
Commented by mr W last updated on 01/Dec/24
이것이 당신이 기대했던 것입니까?
Commented by issac last updated on 03/Dec/24
한국인임?
Commented by mr W last updated on 03/Dec/24

$${maybe} \\ $$
