
Question Number 4589 by FilupSmith last updated on 09/Feb/16
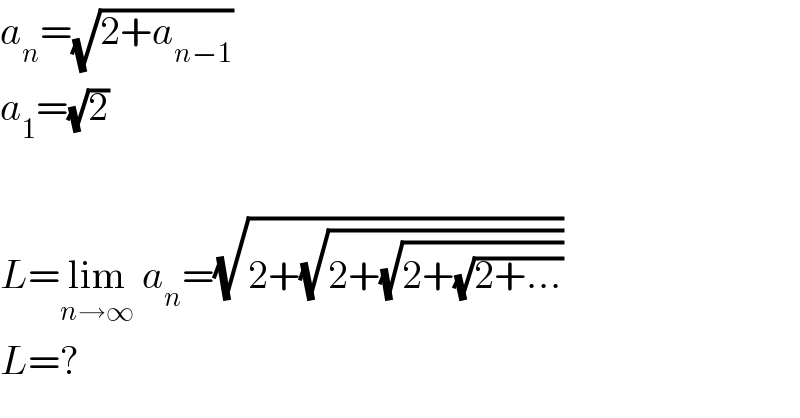
$${a}_{{n}} =\sqrt{\mathrm{2}+{a}_{{n}−\mathrm{1}} } \\ $$$${a}_{\mathrm{1}} =\sqrt{\mathrm{2}} \\ $$$$ \\ $$$${L}=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:{a}_{{n}} =\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+...}}}} \\ $$$${L}=? \\ $$
Answered by Rasheed Soomro last updated on 09/Feb/16

$${a}_{{n}} =\sqrt{\mathrm{2}+{a}_{{n}−\mathrm{1}} } \\ $$$${a}_{\mathrm{1}} =\mathrm{2} \\ $$$${a}_{\mathrm{2}} =\sqrt{\mathrm{2}+{a}_{\mathrm{1}} }=\sqrt{\mathrm{2}+\mathrm{2}}=\mathrm{2} \\ $$$${a}_{\mathrm{3}} =\sqrt{\mathrm{2}+{a}_{\mathrm{2}} }=\sqrt{\mathrm{2}+\mathrm{2}}=\mathrm{2} \\ $$$${This}\:{suggests}\:{that} \\ $$$${a}_{{n}} =\mathrm{2} \\ $$$${How}\:{a}_{{n}} =\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+...}}}}\:\:\:? \\ $$$$.................................................... \\ $$$${Answer}\:{for}\:{corrected}\:{question} \\ $$$${a}_{{n}} =\sqrt{\mathrm{2}+{a}_{{n}−\mathrm{1}} } \\ $$$${a}_{\mathrm{1}} =\sqrt{\mathrm{2}} \\ $$$${L}=\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+...}}}}\: \\ $$$${L}^{\mathrm{2}} =\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+...}}}}\: \\ $$$${L}^{\mathrm{2}} =\mathrm{2}+{L} \\ $$$${L}^{\mathrm{2}} −{L}−\mathrm{2}=\mathrm{0} \\ $$$$\left({L}−\mathrm{2}\right)\left({L}+\mathrm{1}\right)=\mathrm{0} \\ $$$${L}=\mathrm{2}\:\:\mid\:\:{L}=−\mathrm{1} \\ $$$$\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+...}}}}\:\:\:{may}\:{not}\:{be}\:{negative} \\ $$$${and}\:\:{there}\:{is}\:{also}\:{chance}\:{of}\:{extraneous} \\ $$$${roots},\:{so}\:{I}\:{think}\:−\mathrm{1}\:{is}\:{extraneous}\:{root}. \\ $$$${So}\:{L}=\mathrm{2} \\ $$
Commented by FilupSmith last updated on 09/Feb/16

$${sorry}\:{i}\:{meant} \\ $$$${a}_{\mathrm{1}} =\sqrt{\mathrm{2}} \\ $$
