Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 94382 by frc2crc last updated on 18/May/20

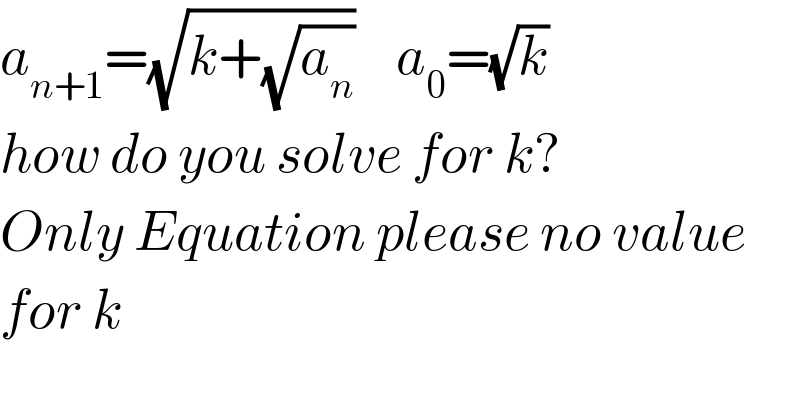
a_(n+1) =(√(k+(√a_n ))) a_0 =(√k) how do you solve for k? Only Equation please no value for k

$${a}_{{n}+\mathrm{1}} =\sqrt{{k}+\sqrt{{a}_{{n}} }}\:\:\:\:{a}_{\mathrm{0}} =\sqrt{{k}} \\ $$$${how}\:{do}\:{you}\:{solve}\:{for}\:{k}? \\ $$$${Only}\:{Equation}\:{please}\:{no}\:{value} \\ $$$${for}\:{k} \\ $$

Commented by prakash jain last updated on 18/May/20

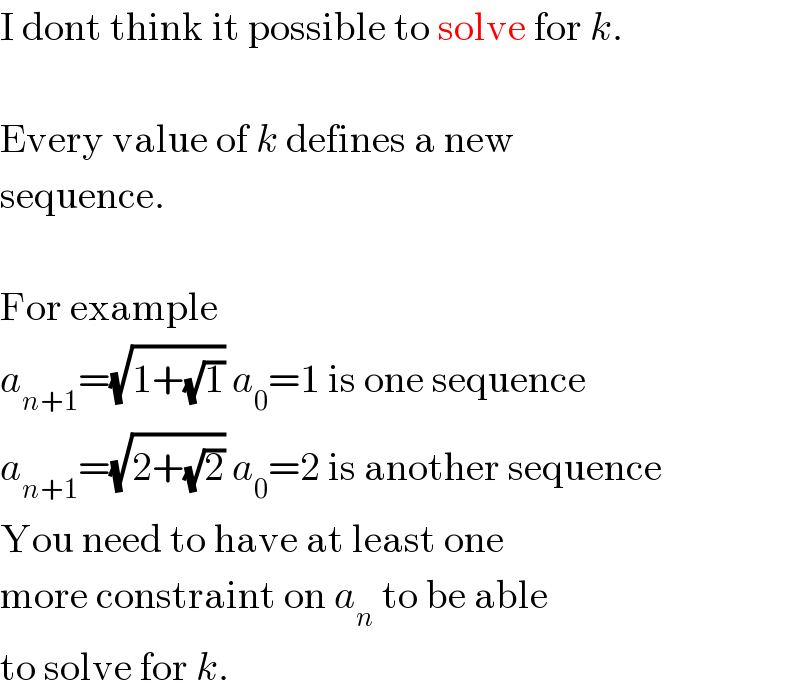
I dont think it possible to solve for k. Every value of k defines a new sequence. For example a_(n+1) =(√(1+(√1))) a_0 =1 is one sequence a_(n+1) =(√(2+(√2))) a_0 =2 is another sequence You need to have at least one more constraint on a_n to be able to solve for k.

$$\mathrm{I}\:\mathrm{dont}\:\mathrm{think}\:\mathrm{it}\:\mathrm{possible}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{for}\:{k}. \\ $$$$ \\ $$$$\mathrm{Every}\:\mathrm{value}\:\mathrm{of}\:{k}\:\mathrm{defines}\:\mathrm{a}\:\mathrm{new} \\ $$$$\mathrm{sequence}. \\ $$$$ \\ $$$$\mathrm{For}\:\mathrm{example} \\ $$$${a}_{{n}+\mathrm{1}} =\sqrt{\mathrm{1}+\sqrt{\mathrm{1}}}\:{a}_{\mathrm{0}} =\mathrm{1}\:\mathrm{is}\:\mathrm{one}\:\mathrm{sequence} \\ $$$${a}_{{n}+\mathrm{1}} =\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}\:{a}_{\mathrm{0}} =\mathrm{2}\:\mathrm{is}\:\mathrm{another}\:\mathrm{sequence} \\ $$$$\mathrm{You}\:\mathrm{need}\:\mathrm{to}\:\mathrm{have}\:\mathrm{at}\:\mathrm{least}\:\mathrm{one} \\ $$$$\mathrm{more}\:\mathrm{constraint}\:\mathrm{on}\:{a}_{{n}} \:\mathrm{to}\:\mathrm{be}\:\mathrm{able} \\ $$$$\mathrm{to}\:\mathrm{solve}\:\mathrm{for}\:{k}. \\ $$

Commented by mr W last updated on 18/May/20

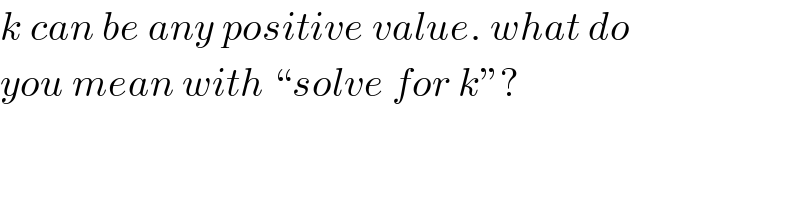
k can be any positive value. what do you mean with “solve for k”?

$${k}\:{can}\:{be}\:{any}\:{positive}\:{value}.\:{what}\:{do} \\ $$$${you}\:{mean}\:{with}\:``{solve}\:{for}\:{k}''? \\ $$

Answered by mathmax by abdo last updated on 20/May/20

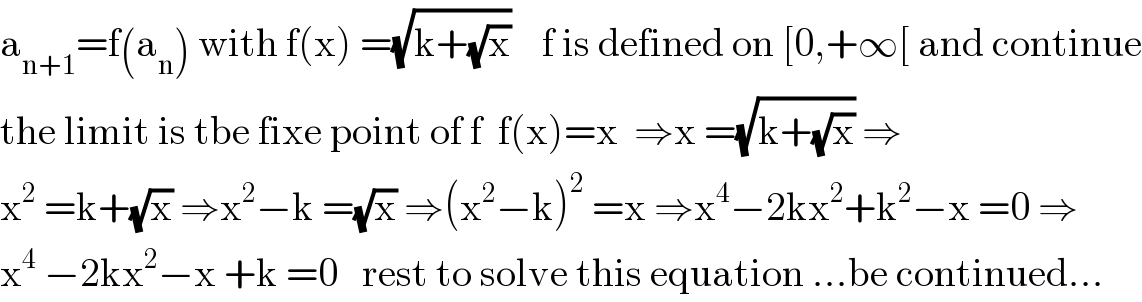
a_(n+1) =f(a_n ) with f(x) =(√(k+(√x))) f is defined on [0,+∞[ and continue the limit is tbe fixe point of f f(x)=x ⇒x =(√(k+(√x))) ⇒ x^2 =k+(√x) ⇒x^2 −k =(√x) ⇒(x^2 −k)^2 =x ⇒x^4 −2kx^2 +k^2 −x =0 ⇒ x^4 −2kx^2 −x +k =0 rest to solve this equation ...be continued...

$$\mathrm{a}_{\mathrm{n}+\mathrm{1}} =\mathrm{f}\left(\mathrm{a}_{\mathrm{n}} \right)\:\mathrm{with}\:\mathrm{f}\left(\mathrm{x}\right)\:=\sqrt{\mathrm{k}+\sqrt{\mathrm{x}}}\:\:\:\:\mathrm{f}\:\mathrm{is}\:\mathrm{defined}\:\mathrm{on}\:\left[\mathrm{0},+\infty\left[\:\mathrm{and}\:\mathrm{continue}\right.\right. \\ $$$$\mathrm{the}\:\mathrm{limit}\:\mathrm{is}\:\mathrm{tbe}\:\mathrm{fixe}\:\mathrm{point}\:\mathrm{of}\:\mathrm{f}\:\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{x}\:\:\Rightarrow\mathrm{x}\:=\sqrt{\mathrm{k}+\sqrt{\mathrm{x}}}\:\Rightarrow \\ $$$$\mathrm{x}^{\mathrm{2}} \:=\mathrm{k}+\sqrt{\mathrm{x}}\:\Rightarrow\mathrm{x}^{\mathrm{2}} −\mathrm{k}\:=\sqrt{\mathrm{x}}\:\Rightarrow\left(\mathrm{x}^{\mathrm{2}} −\mathrm{k}\right)^{\mathrm{2}} \:=\mathrm{x}\:\Rightarrow\mathrm{x}^{\mathrm{4}} −\mathrm{2kx}^{\mathrm{2}} +\mathrm{k}^{\mathrm{2}} −\mathrm{x}\:=\mathrm{0}\:\Rightarrow \\ $$$$\mathrm{x}^{\mathrm{4}} \:−\mathrm{2kx}^{\mathrm{2}} −\mathrm{x}\:+\mathrm{k}\:=\mathrm{0}\:\:\:\mathrm{rest}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{this}\:\mathrm{equation}\:...\mathrm{be}\:\mathrm{continued}... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com