
Question Number 123548 by bramlexs22 last updated on 26/Nov/20

$${a}\:{man}\:\mathrm{6}\:{ft}\:{tall}\:{walks}\:{at}\:{a}\:{rate} \\ $$$${of}\:\mathrm{7}\:{ft}/{sec}\:{away}\:{from}\:{a}\:{lamppost} \\ $$$${that}\:{is}\:\mathrm{14}\:{ft}\:{hight}. \\ $$$${at}\:{what}\:{rate}\:{is}\:{the}\:{lenght}\:{of}\:{his} \\ $$$${shadow}\:{charging}\:{when}\:{he}\:{is}\:\mathrm{30}\:{ft}\: \\ $$$${away}\:{from}\:{the}\:{lamppost} \\ $$
Commented by bramlexs22 last updated on 26/Nov/20
$${any}\:{one}\:{help}\:{me} \\ $$
Answered by mr W last updated on 26/Nov/20
Commented by mr W last updated on 26/Nov/20
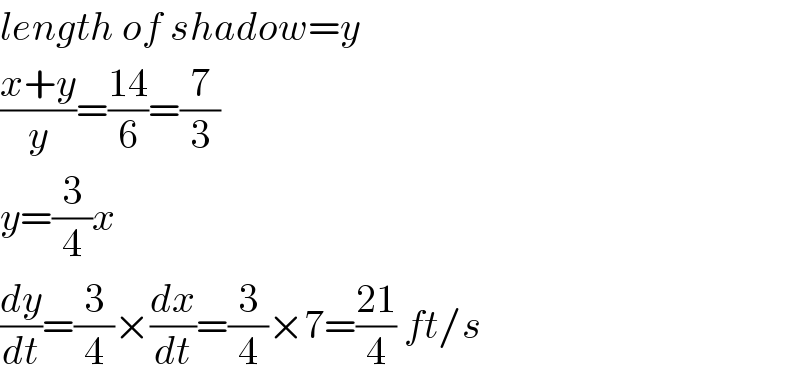
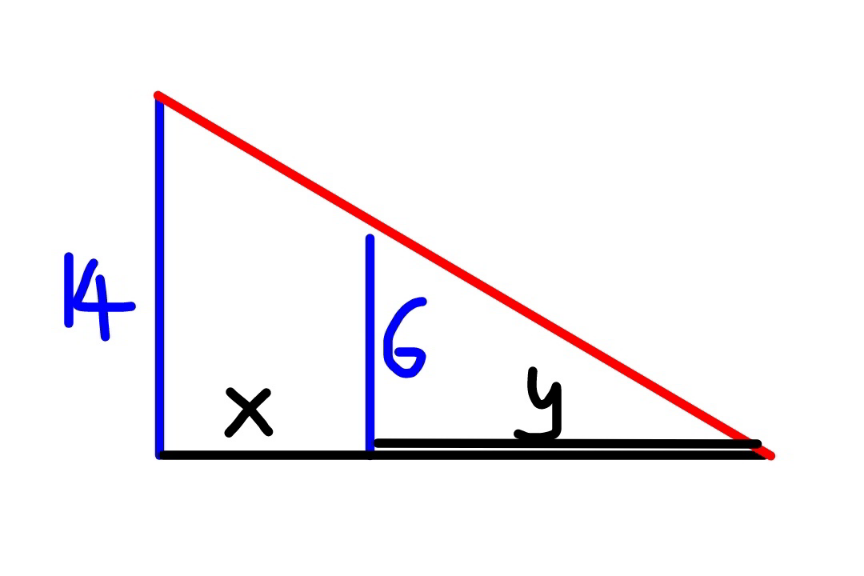
$${length}\:{of}\:{shadow}={y} \\ $$$$\frac{{x}+{y}}{{y}}=\frac{\mathrm{14}}{\mathrm{6}}=\frac{\mathrm{7}}{\mathrm{3}} \\ $$$${y}=\frac{\mathrm{3}}{\mathrm{4}}{x} \\ $$$$\frac{{dy}}{{dt}}=\frac{\mathrm{3}}{\mathrm{4}}×\frac{{dx}}{{dt}}=\frac{\mathrm{3}}{\mathrm{4}}×\mathrm{7}=\frac{\mathrm{21}}{\mathrm{4}}\:{ft}/{s} \\ $$
Commented by bramlexs22 last updated on 26/Nov/20

$${thank}\:{you}\:{sir} \\ $$
Commented by bramlexs22 last updated on 26/Nov/20
Why is the 30 ft / sec information not being used sir?
Commented by mr W last updated on 26/Nov/20

$${the}\:{rate}\:{of}\:{changing}\:{is}\:{constant}, \\ $$$${no}\:{matter}\:{where}\:{the}\:{man}\:{is}. \\ $$
