
Question Number 196399 by tri26112004 last updated on 24/Aug/23
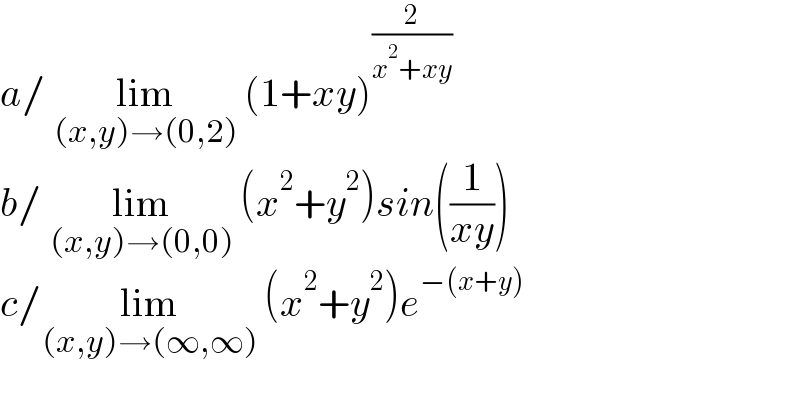
$${a}/\:\underset{\left({x},{y}\right)\rightarrow\left(\mathrm{0},\mathrm{2}\right)} {\mathrm{lim}}\:\left(\mathrm{1}+{xy}\right)^{\frac{\mathrm{2}}{{x}^{\mathrm{2}} +{xy}}} \\ $$$${b}/\:\underset{\left({x},{y}\right)\rightarrow\left(\mathrm{0},\mathrm{0}\right)} {\mathrm{lim}}\:\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right){sin}\left(\frac{\mathrm{1}}{{xy}}\right) \\ $$$${c}/\underset{\left({x},{y}\right)\rightarrow\left(\infty,\infty\right)} {\mathrm{lim}}\:\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right){e}^{−\left({x}+{y}\right)} \\ $$
Answered by MM42 last updated on 24/Aug/23
![a)lim_((x,y)→(0,2)) [(1+xy)^(1/(xy)) ]^( ((2xy)/(x^2 +xy))) lim_((x,y)→(0,2)) [(1+xy)^(1/(xy)) ]^( ((2y)/(x+y))) =e^2 b) −(x^2 +y^2 )≤sin((1/(xy)))≤(x^2 +y^2 ) ⇒ lim_((x,y)→(0,0)) −(x^2 +y^2 )≤lim_((x,u)→(0,0)) sin((1/(xy)))≤lim_((x,y)→(0,0)) (x^2 +y^2 ) ⇒Ans=0 c)if x=y>0 ⇒ lim_(x→+∞) ((2x^2 )/e^(2x) ) =0 if x=y<0 ⇒ lim_(x→+∞) 2x^2 e^(2x) =∞](Q196433.png)
$$\left.{a}\right){lim}_{\left({x},{y}\right)\rightarrow\left(\mathrm{0},\mathrm{2}\right)} \left[\left(\mathrm{1}+{xy}\right)^{\frac{\mathrm{1}}{{xy}}} \:\:\right]^{\:\frac{\mathrm{2}{xy}}{{x}^{\mathrm{2}} +{xy}}} \: \\ $$$${lim}_{\left({x},{y}\right)\rightarrow\left(\mathrm{0},\mathrm{2}\right)} \left[\left(\mathrm{1}+{xy}\right)^{\frac{\mathrm{1}}{{xy}}} \:\:\right]^{\:\frac{\mathrm{2}{y}}{{x}+{y}}} \:={e}^{\mathrm{2}} \\ $$$$ \\ $$$$\left.{b}\right)\:\:\:−\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)\leqslant{sin}\left(\frac{\mathrm{1}}{{xy}}\right)\leqslant\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right) \\ $$$$\Rightarrow\:\:{lim}_{\left({x},{y}\right)\rightarrow\left(\mathrm{0},\mathrm{0}\right)} \:−\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)\leqslant{lim}_{\left({x},{u}\right)\rightarrow\left(\mathrm{0},\mathrm{0}\right)} \:{sin}\left(\frac{\mathrm{1}}{{xy}}\right)\leqslant{lim}_{\left({x},{y}\right)\rightarrow\left(\mathrm{0},\mathrm{0}\right)} \:\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right) \\ $$$$\Rightarrow{Ans}=\mathrm{0} \\ $$$$\left.{c}\right){if}\:\:{x}={y}>\mathrm{0}\:\Rightarrow\:{lim}_{{x}\rightarrow+\infty} \:\frac{\mathrm{2}{x}^{\mathrm{2}} }{{e}^{\mathrm{2}{x}} }\:=\mathrm{0} \\ $$$${if}\:\:{x}={y}<\mathrm{0}\:\Rightarrow\:{lim}_{{x}\rightarrow+\infty} \:\mathrm{2}{x}^{\mathrm{2}} \:{e}^{\mathrm{2}{x}} =\infty \\ $$$$ \\ $$$$ \\ $$
