
Question Number 212992 by CrispyXYZ last updated on 28/Oct/24
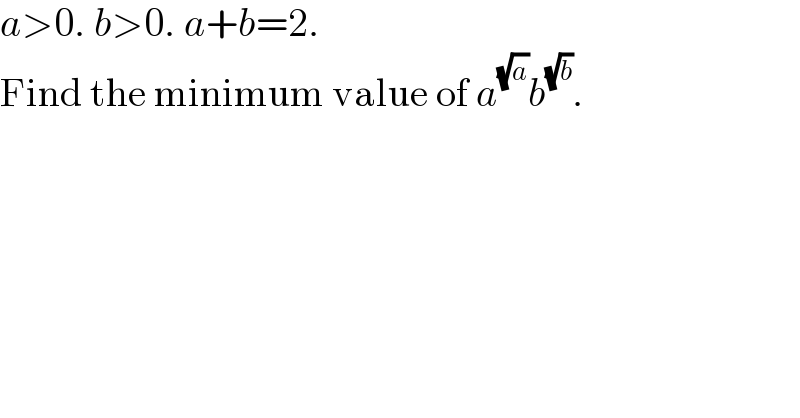
$${a}>\mathrm{0}.\:{b}>\mathrm{0}.\:{a}+{b}=\mathrm{2}. \\ $$$$\mathrm{Find}\:\mathrm{the}\:\mathrm{minimum}\:\mathrm{value}\:\mathrm{of}\:{a}^{\sqrt{{a}}} {b}^{\sqrt{{b}}} . \\ $$
Answered by Ghisom last updated on 28/Oct/24
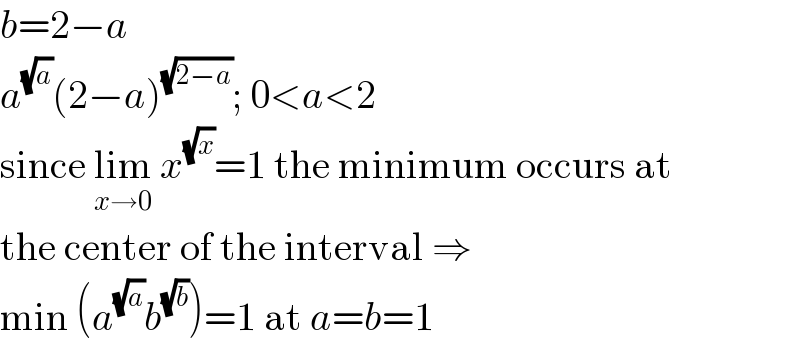
$${b}=\mathrm{2}−{a} \\ $$$${a}^{\sqrt{{a}}} \left(\mathrm{2}−{a}\right)^{\sqrt{\mathrm{2}−{a}}} ;\:\mathrm{0}<{a}<\mathrm{2} \\ $$$$\mathrm{since}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:{x}^{\sqrt{{x}}} =\mathrm{1}\:\mathrm{the}\:\mathrm{minimum}\:\mathrm{occurs}\:\mathrm{at} \\ $$$$\mathrm{the}\:\mathrm{center}\:\mathrm{of}\:\mathrm{the}\:\mathrm{interval}\:\Rightarrow \\ $$$$\mathrm{min}\:\left({a}^{\sqrt{{a}}} {b}^{\sqrt{{b}}} \right)=\mathrm{1}\:\mathrm{at}\:{a}={b}=\mathrm{1} \\ $$
