Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 188284 by Humble last updated on 27/Feb/23

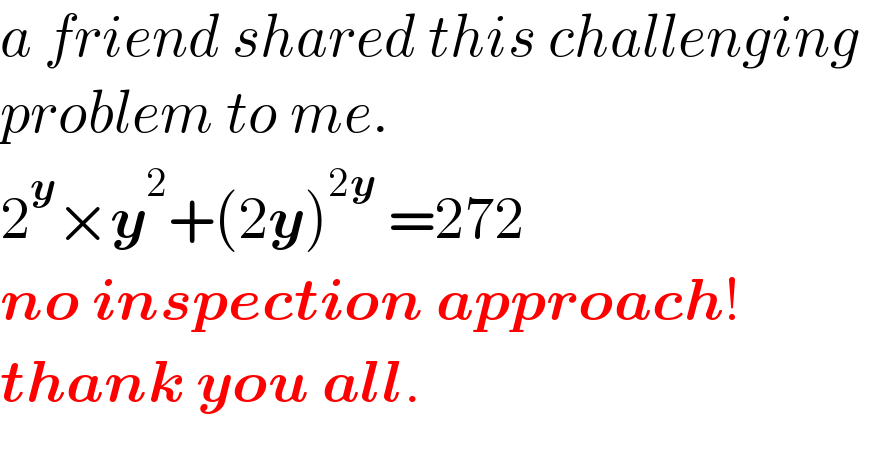
a friend shared this challenging problem to me. 2^y ×y^2 +(2y)^(2y) =272 no inspection approach! thank you all.

$${a}\:{friend}\:{shared}\:{this}\:{challenging}\: \\ $$$${problem}\:{to}\:{me}. \\ $$$$\mathrm{2}^{\boldsymbol{{y}}} ×\boldsymbol{{y}}^{\mathrm{2}} +\left(\mathrm{2}\boldsymbol{{y}}\right)^{\mathrm{2}\boldsymbol{{y}}} \:=\mathrm{272} \\ $$$$\boldsymbol{{no}}\:\boldsymbol{{inspection}}\:\boldsymbol{{approach}}! \\ $$$$\boldsymbol{{thank}}\:\boldsymbol{{you}}\:\boldsymbol{{all}}. \\ $$

Commented by Frix last updated on 27/Feb/23

I don′t think there′s a method for an exact solution. You can approximate or use your brains. I showed that 2^y ×y^2 +(2y)^(2y) =16+256 ⇒ y=2 If you don′t like this approach, find another one!

$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{think}\:\mathrm{there}'\mathrm{s}\:\mathrm{a}\:\mathrm{method}\:\mathrm{for}\:\mathrm{an}\:\mathrm{exact} \\ $$$$\mathrm{solution}.\:\mathrm{You}\:\mathrm{can}\:\mathrm{approximate}\:\mathrm{or}\:\mathrm{use} \\ $$$$\mathrm{your}\:\mathrm{brains}.\:\mathrm{I}\:\mathrm{showed}\:\mathrm{that} \\ $$$$\mathrm{2}^{{y}} ×{y}^{\mathrm{2}} +\left(\mathrm{2}{y}\right)^{\mathrm{2}{y}} =\mathrm{16}+\mathrm{256} \\ $$$$\Rightarrow\:{y}=\mathrm{2} \\ $$$$\mathrm{If}\:\mathrm{you}\:\mathrm{don}'\mathrm{t}\:\mathrm{like}\:\mathrm{this}\:\mathrm{approach},\:\mathrm{find}\:\mathrm{another} \\ $$$$\mathrm{one}! \\ $$

Answered by a.lgnaoui last updated on 28/Feb/23

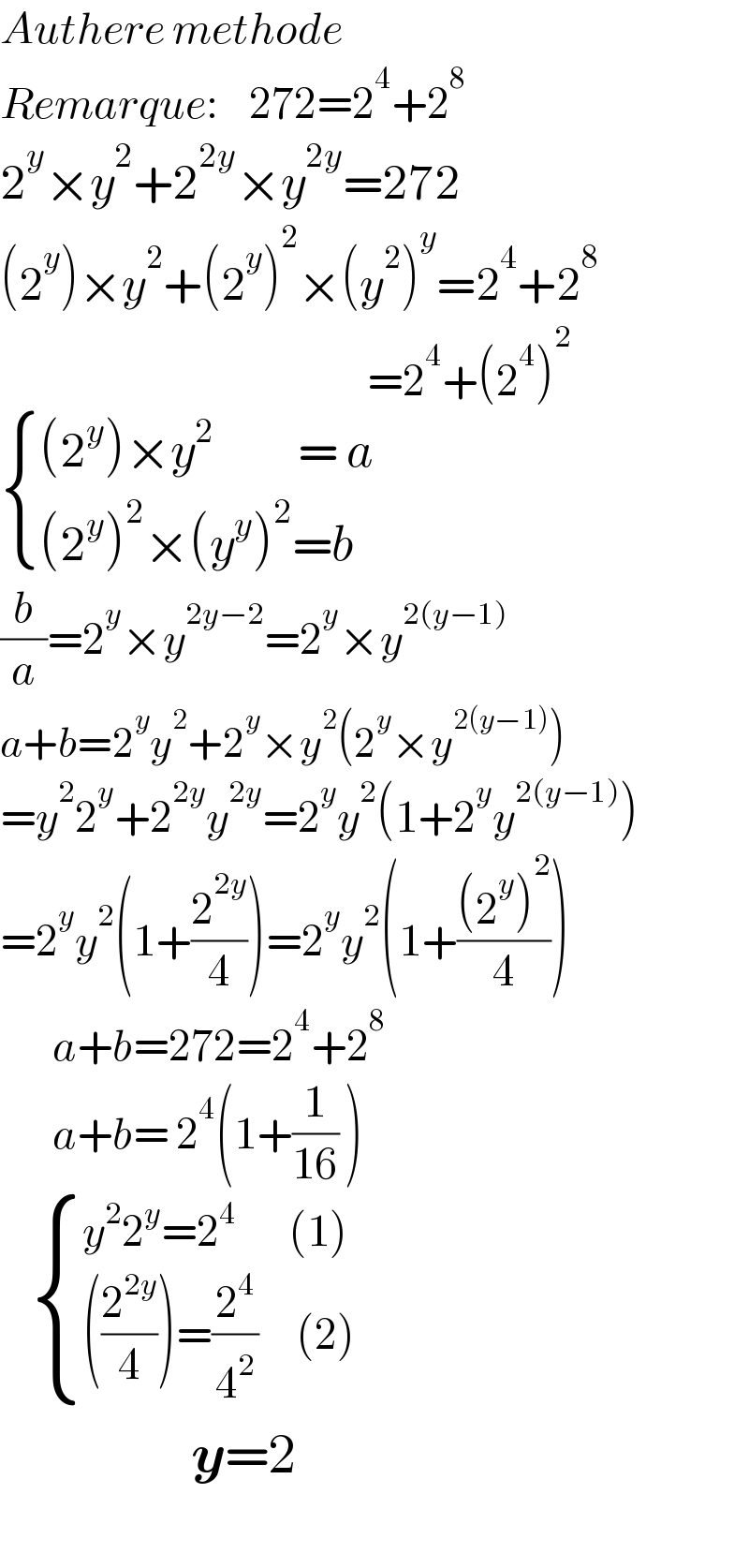
Authere methode Remarque: 272=2^4 +2^8 2^y ×y^2 +2^(2y) ×y^(2y) =272 (2^y )×y^2 +(2^y )^2 ×(y^2 )^y =2^4 +2^8 =2^4 +(2^4 )^2 { (((2^y )×y^2 = a)),(((2^y )^2 ×(y^y )^2 =b)) :} (b/a)=2^y ×y^(2y−2) =2^y ×y^(2(y−1)) a+b=2^y y^2 +2^y ×y^2 (2^y ×y^(2(y−1)) ) =y^2 2^y +2^(2y) y^(2y) =2^y y^2 (1+2^y y^(2(y−1)) ) =2^y y^2 (1+(2^(2y) /4))=2^y y^2 (1+(((2^y )^2 )/4)) a+b=272=2^4 +2^8 a+b= 2^4 (1+(1/(16)) ) { ((y^2 2^y =2^4 (1))),((((2^(2y) /4))=(2^4 /4^2 ) (2))) :} y=2

$${Authere}\:{methode} \\ $$$${Remarque}:\:\:\:\:\mathrm{272}=\mathrm{2}^{\mathrm{4}} +\mathrm{2}^{\mathrm{8}} \\ $$$$\mathrm{2}^{{y}} ×{y}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}{y}} ×{y}^{\mathrm{2}{y}} =\mathrm{272} \\ $$$$\left(\mathrm{2}^{{y}} \right)×{y}^{\mathrm{2}} +\left(\mathrm{2}^{{y}} \right)^{\mathrm{2}} ×\left({y}^{\mathrm{2}} \right)^{{y}} =\mathrm{2}^{\mathrm{4}} +\mathrm{2}^{\mathrm{8}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}^{\mathrm{4}} +\left(\mathrm{2}^{\mathrm{4}} \right)^{\mathrm{2}} \\ $$$$\begin{cases}{\left(\mathrm{2}^{{y}} \right)×{y}^{\mathrm{2}} \:\:\:\:\:\:\:\:\:=\:{a}}\\{\left(\mathrm{2}^{{y}} \right)^{\mathrm{2}} ×\left({y}^{{y}} \right)^{\mathrm{2}} ={b}}\end{cases} \\ $$$$\frac{{b}}{{a}}=\mathrm{2}^{{y}} ×{y}^{\mathrm{2}{y}−\mathrm{2}} =\mathrm{2}^{{y}} ×{y}^{\mathrm{2}\left({y}−\mathrm{1}\right)} \\ $$$${a}+{b}=\mathrm{2}^{{y}} {y}^{\mathrm{2}} +\mathrm{2}^{{y}} ×{y}^{\mathrm{2}} \left(\mathrm{2}^{{y}} ×{y}^{\mathrm{2}\left({y}−\mathrm{1}\right)} \right) \\ $$$$={y}^{\mathrm{2}} \mathrm{2}^{{y}} +\mathrm{2}^{\mathrm{2}{y}} {y}^{\mathrm{2}{y}} =\mathrm{2}^{{y}} {y}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{2}^{{y}} {y}^{\mathrm{2}\left({y}−\mathrm{1}\right)} \right) \\ $$$$=\mathrm{2}^{{y}} {y}^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{2}^{\mathrm{2}{y}} }{\mathrm{4}}\right)=\mathrm{2}^{{y}} {y}^{\mathrm{2}} \left(\mathrm{1}+\frac{\left(\mathrm{2}^{{y}} \right)^{\mathrm{2}} }{\mathrm{4}}\right) \\ $$$$\:\:\:\:\:\:\:{a}+{b}=\mathrm{272}=\mathrm{2}^{\mathrm{4}} +\mathrm{2}^{\mathrm{8}} \\ $$$$\:\:\:\:\:\:\:{a}+{b}=\:\mathrm{2}^{\mathrm{4}} \left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{16}}\:\right) \\ $$$$\:\:\:\:\begin{cases}{{y}^{\mathrm{2}} \mathrm{2}^{{y}} =\mathrm{2}^{\mathrm{4}} \:\:\:\:\:\:\:\left(\mathrm{1}\right)}\\{\left(\frac{\mathrm{2}^{\mathrm{2}{y}} }{\mathrm{4}}\right)=\frac{\mathrm{2}^{\mathrm{4}} }{\mathrm{4}^{\mathrm{2}} }\:\:\:\:\:\left(\mathrm{2}\right)}\end{cases} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{{y}}=\mathrm{2} \\ $$$$\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com