Question Number 196049 by CrispyXYZ last updated on 17/Aug/23
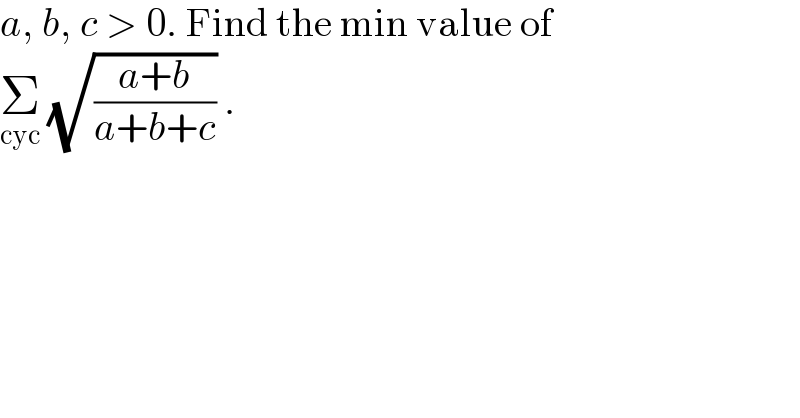
$${a},\:{b},\:{c}\:>\:\mathrm{0}.\:\mathrm{Find}\:\mathrm{the}\:\mathrm{min}\:\mathrm{value}\:\mathrm{of} \\ $$$$\underset{\mathrm{cyc}} {\sum}\:\sqrt{\frac{{a}+{b}}{{a}+{b}+{c}}}\:. \\ $$
Commented by Frix last updated on 17/Aug/23
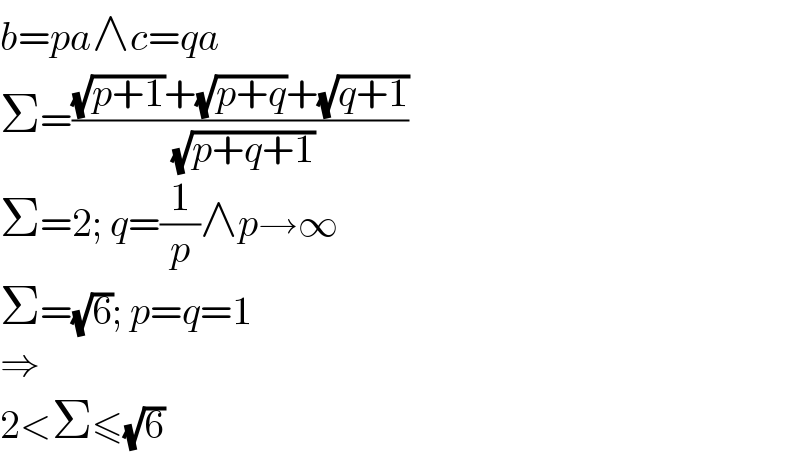
$${b}={pa}\wedge{c}={qa} \\ $$$$\Sigma=\frac{\sqrt{{p}+\mathrm{1}}+\sqrt{{p}+{q}}+\sqrt{{q}+\mathrm{1}}}{\:\sqrt{{p}+{q}+\mathrm{1}}} \\ $$$$\Sigma=\mathrm{2};\:{q}=\frac{\mathrm{1}}{{p}}\wedge{p}\rightarrow\infty \\ $$$$\Sigma=\sqrt{\mathrm{6}};\:{p}={q}=\mathrm{1} \\ $$$$\Rightarrow \\ $$$$\mathrm{2}<\Sigma\leqslant\sqrt{\mathrm{6}} \\ $$
Answered by mr W last updated on 17/Aug/23

$${S}=\frac{\sqrt{{a}+{b}}+\sqrt{{b}+{c}}+\sqrt{{c}+{a}}}{\:\sqrt{{a}+{b}+{c}}} \\ $$$$=\frac{\sqrt{\mathrm{2}}\left(\sqrt{{a}+{b}}+\sqrt{{b}+{c}}+\sqrt{{c}+{a}}\right)}{\:\sqrt{\mathrm{2}\left({a}+{b}+{c}\right)}} \\ $$$$=\frac{\sqrt{\mathrm{2}}\left(\sqrt{{a}+{b}}+\sqrt{{b}+{c}}+\sqrt{{c}+{a}}\right)}{\:\sqrt{\left({a}+{b}\right)+\left({b}+{c}\right)+\left({c}+{a}\right)}} \\ $$$$=\frac{\sqrt{\mathrm{2}}\left({x}+{y}+{z}\right)}{\:\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} }}\:\left({with}\:{x}=\sqrt{{a}+{b}}>\mathrm{0}...\right) \\ $$$$=\frac{\sqrt{\mathrm{6}}\left(\mathrm{1}×{x}+\mathrm{1}×{y}+\mathrm{1}×{z}\right)}{\:\sqrt{\mathrm{3}}×\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} }} \\ $$$$=\sqrt{\mathrm{6}}\:\mathrm{cos}\:\theta \\ $$$$\theta={angle}\:{between}\:{vectors}\:\left(\mathrm{1},\mathrm{1},\mathrm{1}\right)\:{and}\:\left({x},{y},{z}\right) \\ $$$$\mathrm{0}\leqslant\theta<\mathrm{cos}^{−\mathrm{1}} \sqrt{\frac{\mathrm{2}}{\mathrm{3}}} \\ $$$$\Rightarrow\mathrm{2}<{S}\leqslant\sqrt{\mathrm{6}} \\ $$$${mininum}\:{doesn}'{t}\:{exist}. \\ $$
Commented by mr W last updated on 18/Aug/23