Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 193875 by Subhi last updated on 22/Jun/23

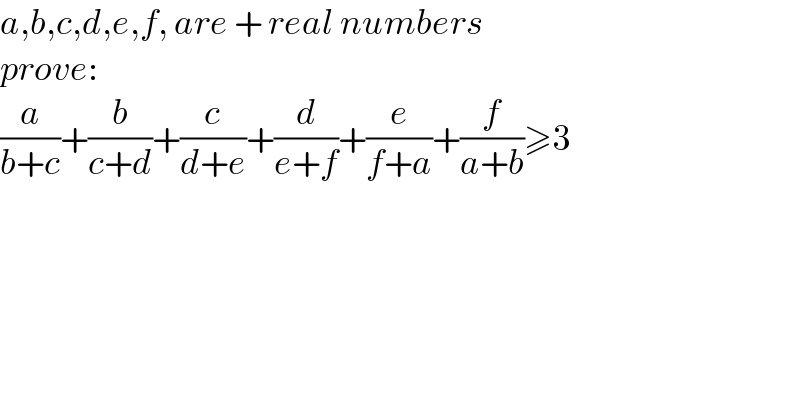
a,b,c,d,e,f, are + real numbers prove: (a/(b+c))+(b/(c+d))+(c/(d+e))+(d/(e+f))+(e/(f+a))+(f/(a+b))≥3

$${a},{b},{c},{d},{e},{f},\:{are}\:+\:{real}\:{numbers} \\ $$$${prove}: \\ $$$$\frac{{a}}{{b}+{c}}+\frac{{b}}{{c}+{d}}+\frac{{c}}{{d}+{e}}+\frac{{d}}{{e}+{f}}+\frac{{e}}{{f}+{a}}+\frac{{f}}{{a}+{b}}\geqslant\mathrm{3} \\ $$

Answered by deleteduser1 last updated on 23/Jun/23

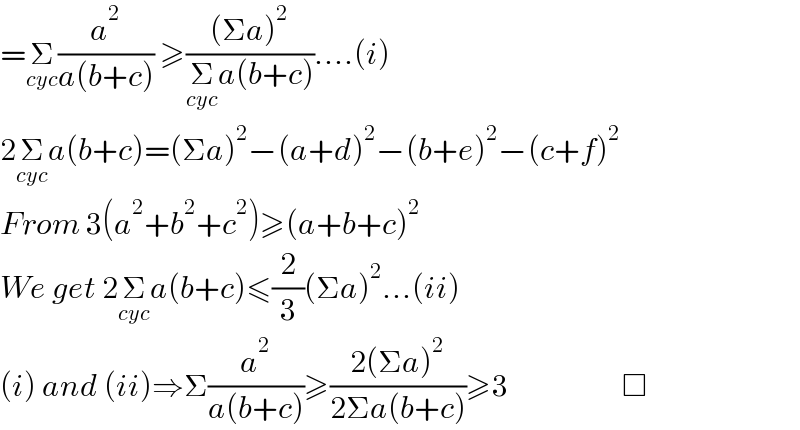
=Σ_(cyc) (a^2 /(a(b+c))) ≥(((Σa)^2 )/(Σ_(cyc) a(b+c)))....(i) 2Σ_(cyc) a(b+c)=(Σa)^2 −(a+d)^2 −(b+e)^2 −(c+f)^2 From 3(a^2 +b^2 +c^2 )≥(a+b+c)^2 We get 2Σ_(cyc) a(b+c)≤(2/3)(Σa)^2 ...(ii) (i) and (ii)⇒Σ(a^2 /(a(b+c)))≥((2(Σa)^2 )/(2Σa(b+c)))≥3 □

$$=\underset{{cyc}} {\sum}\frac{{a}^{\mathrm{2}} }{{a}\left({b}+{c}\right)}\:\geqslant\frac{\left(\Sigma{a}\right)^{\mathrm{2}} }{\underset{{cyc}} {\sum}{a}\left({b}+{c}\right)}....\left({i}\right) \\ $$$$\mathrm{2}\underset{{cyc}} {\sum}{a}\left({b}+{c}\right)=\left(\Sigma{a}\right)^{\mathrm{2}} −\left({a}+{d}\right)^{\mathrm{2}} −\left({b}+{e}\right)^{\mathrm{2}} −\left({c}+{f}\right)^{\mathrm{2}} \\ $$$${From}\:\mathrm{3}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)\geqslant\left({a}+{b}+{c}\right)^{\mathrm{2}} \\ $$$${We}\:{get}\:\mathrm{2}\underset{{cyc}} {\sum}{a}\left({b}+{c}\right)\leqslant\frac{\mathrm{2}}{\mathrm{3}}\left(\Sigma{a}\right)^{\mathrm{2}} ...\left({ii}\right) \\ $$$$\left({i}\right)\:{and}\:\left({ii}\right)\Rightarrow\Sigma\frac{{a}^{\mathrm{2}} }{{a}\left({b}+{c}\right)}\geqslant\frac{\mathrm{2}\left(\Sigma{a}\right)^{\mathrm{2}} }{\mathrm{2}\Sigma{a}\left({b}+{c}\right)}\geqslant\mathrm{3}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Box \\ $$

Commented by Subhi last updated on 23/Jun/23

perfect

$${perfect}\: \\ $$

Answered by Subhi last updated on 23/Jun/23

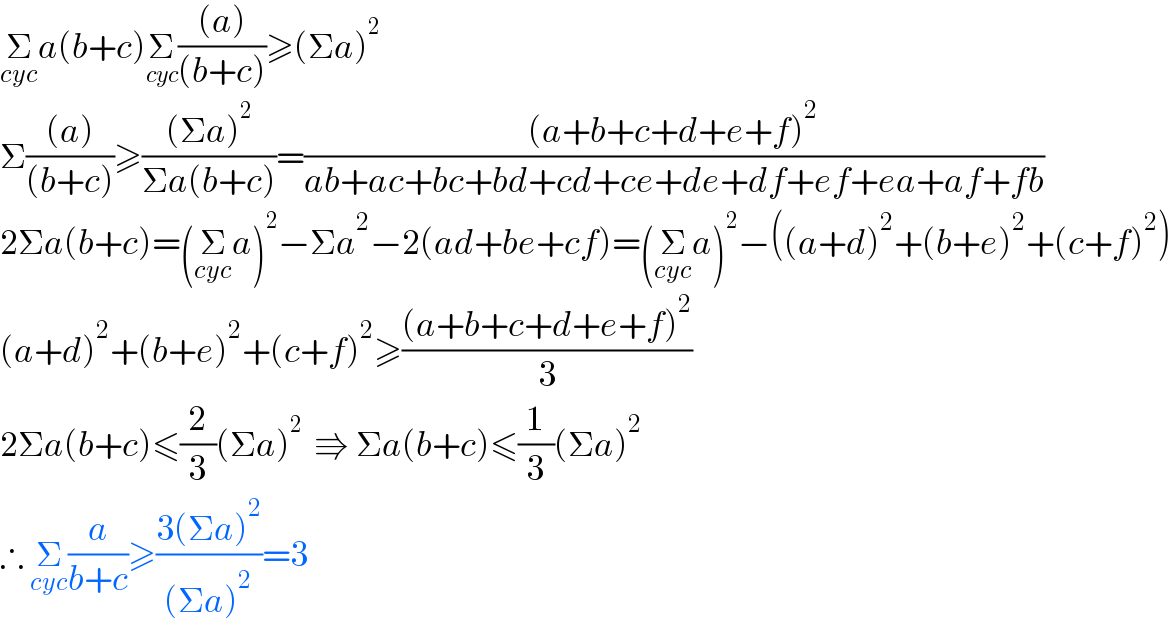
Σ_(cyc) a(b+c)Σ_(cyc) (((a))/((b+c)))≥(Σa)^2 Σ(((a))/((b+c)))≥(((Σa)^2 )/(Σa(b+c)))=(((a+b+c+d+e+f)^2 )/(ab+ac+bc+bd+cd+ce+de+df+ef+ea+af+fb)) 2Σa(b+c)=(Σ_(cyc) a)^2 −Σa^2 −2(ad+be+cf)=(Σ_(cyc) a)^2 −((a+d)^2 +(b+e)^2 +(c+f)^2 ) (a+d)^2 +(b+e)^2 +(c+f)^2 ≥(((a+b+c+d+e+f)^2 )/3) 2Σa(b+c)≤(2/3)(Σa)^2 ⇛ Σa(b+c)≤(1/3)(Σa)^2 ∴ Σ_(cyc) (a/(b+c))≥((3(Σa)^2 )/((Σa)^2 ))=3

$$\underset{{cyc}} {\sum}{a}\left({b}+{c}\right)\underset{{cyc}} {\sum}\frac{\left({a}\right)}{\left({b}+{c}\right)}\geqslant\left(\Sigma{a}\right)^{\mathrm{2}} \\ $$$$\Sigma\frac{\left({a}\right)}{\left({b}+{c}\right)}\geqslant\frac{\left(\Sigma{a}\right)^{\mathrm{2}} }{\Sigma{a}\left({b}+{c}\right)}=\frac{\left({a}+{b}+{c}+{d}+{e}+{f}\right)^{\mathrm{2}} }{{ab}+{ac}+{bc}+{bd}+{cd}+{ce}+{de}+{df}+{ef}+{ea}+{af}+{fb}} \\ $$$$\mathrm{2}\Sigma{a}\left({b}+{c}\right)=\left(\underset{{cyc}} {\sum}{a}\right)^{\mathrm{2}} −\Sigma{a}^{\mathrm{2}} −\mathrm{2}\left({ad}+{be}+{cf}\right)=\left(\underset{{cyc}} {\sum}{a}\right)^{\mathrm{2}} −\left(\left({a}+{d}\right)^{\mathrm{2}} +\left({b}+{e}\right)^{\mathrm{2}} +\left({c}+{f}\right)^{\mathrm{2}} \right) \\ $$$$\left({a}+{d}\right)^{\mathrm{2}} +\left({b}+{e}\right)^{\mathrm{2}} +\left({c}+{f}\right)^{\mathrm{2}} \geqslant\frac{\left({a}+{b}+{c}+{d}+{e}+{f}\right)^{\mathrm{2}} }{\mathrm{3}} \\ $$$$\mathrm{2}\Sigma{a}\left({b}+{c}\right)\leqslant\frac{\mathrm{2}}{\mathrm{3}}\left(\Sigma{a}\right)^{\mathrm{2}} \:\:\Rrightarrow\:\Sigma{a}\left({b}+{c}\right)\leqslant\frac{\mathrm{1}}{\mathrm{3}}\left(\Sigma{a}\right)^{\mathrm{2}} \: \\ $$$$\therefore\:\underset{{cyc}} {\sum}\frac{{a}}{{b}+{c}}\geqslant\frac{\mathrm{3}\left(\Sigma{a}\right)^{\mathrm{2}} }{\left(\Sigma{a}\right)^{\mathrm{2}} }=\mathrm{3} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com