Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 214443 by hardmath last updated on 08/Dec/24

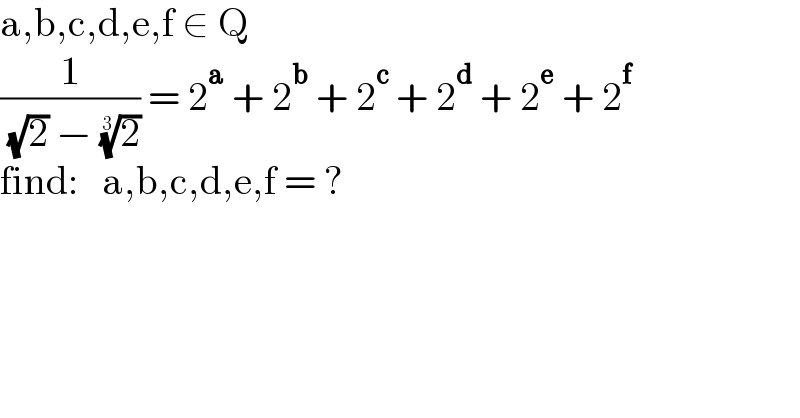
a,b,c,d,e,f ∈ Q (1/( (√2) − (2)^(1/3) )) = 2^a + 2^b + 2^c + 2^d + 2^e + 2^f find: a,b,c,d,e,f = ?

$$\mathrm{a},\mathrm{b},\mathrm{c},\mathrm{d},\mathrm{e},\mathrm{f}\:\in\:\mathrm{Q} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}\:−\:\sqrt[{\mathrm{3}}]{\mathrm{2}}}\:=\:\mathrm{2}^{\boldsymbol{\mathrm{a}}} \:+\:\mathrm{2}^{\boldsymbol{\mathrm{b}}} \:+\:\mathrm{2}^{\boldsymbol{\mathrm{c}}} \:+\:\mathrm{2}^{\boldsymbol{\mathrm{d}}} \:+\:\mathrm{2}^{\boldsymbol{\mathrm{e}}} \:+\:\mathrm{2}^{\boldsymbol{\mathrm{f}}} \\ $$$$\mathrm{find}:\:\:\:\mathrm{a},\mathrm{b},\mathrm{c},\mathrm{d},\mathrm{e},\mathrm{f}\:=\:? \\ $$

Answered by ajfour last updated on 08/Dec/24

(1/(a^3 −a^2 ))=((a^6 +a^4 +a^5 )/(a^9 −a^6 ))=((2+2^(2/3) +2^(5/6) )/(2(√2)−2)) =(((2+2^(2/3) +2^(5/6) )(2(√2)+2))/4) =(1+(1/2^(1/3) )+(1/2^(1/6) ))(2^(1/2) +1) =1+(1/2^(1/3) )+(1/2^(1/6) )+2^(1/2) +2^(1/6) +2^(1/3) will this do?

$$\frac{\mathrm{1}}{{a}^{\mathrm{3}} −{a}^{\mathrm{2}} }=\frac{{a}^{\mathrm{6}} +{a}^{\mathrm{4}} +{a}^{\mathrm{5}} }{{a}^{\mathrm{9}} −{a}^{\mathrm{6}} }=\frac{\mathrm{2}+\mathrm{2}^{\mathrm{2}/\mathrm{3}} +\mathrm{2}^{\mathrm{5}/\mathrm{6}} }{\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{2}} \\ $$$$=\frac{\left(\mathrm{2}+\mathrm{2}^{\mathrm{2}/\mathrm{3}} +\mathrm{2}^{\mathrm{5}/\mathrm{6}} \right)\left(\mathrm{2}\sqrt{\mathrm{2}}+\mathrm{2}\right)}{\mathrm{4}} \\ $$$$=\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{1}/\mathrm{3}} }+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{1}/\mathrm{6}} }\right)\left(\mathrm{2}^{\mathrm{1}/\mathrm{2}} +\mathrm{1}\right) \\ $$$$=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{1}/\mathrm{3}} }+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{1}/\mathrm{6}} }+\mathrm{2}^{\mathrm{1}/\mathrm{2}} +\mathrm{2}^{\mathrm{1}/\mathrm{6}} +\mathrm{2}^{\mathrm{1}/\mathrm{3}} \\ $$$${will}\:{this}\:{do}? \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com