
Question Number 213417 by hardmath last updated on 04/Nov/24
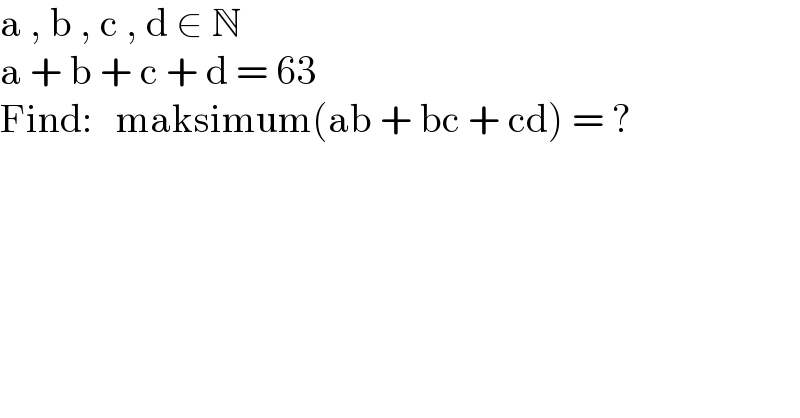
$$\mathrm{a}\:,\:\mathrm{b}\:,\:\mathrm{c}\:,\:\mathrm{d}\:\in\:\mathbb{N} \\ $$$$\mathrm{a}\:+\:\mathrm{b}\:+\:\mathrm{c}\:+\:\mathrm{d}\:=\:\mathrm{63} \\ $$$$\mathrm{Find}:\:\:\:\mathrm{maksimum}\left(\mathrm{ab}\:+\:\mathrm{bc}\:+\:\mathrm{cd}\right)\:=\:? \\ $$
Answered by Frix last updated on 05/Nov/24
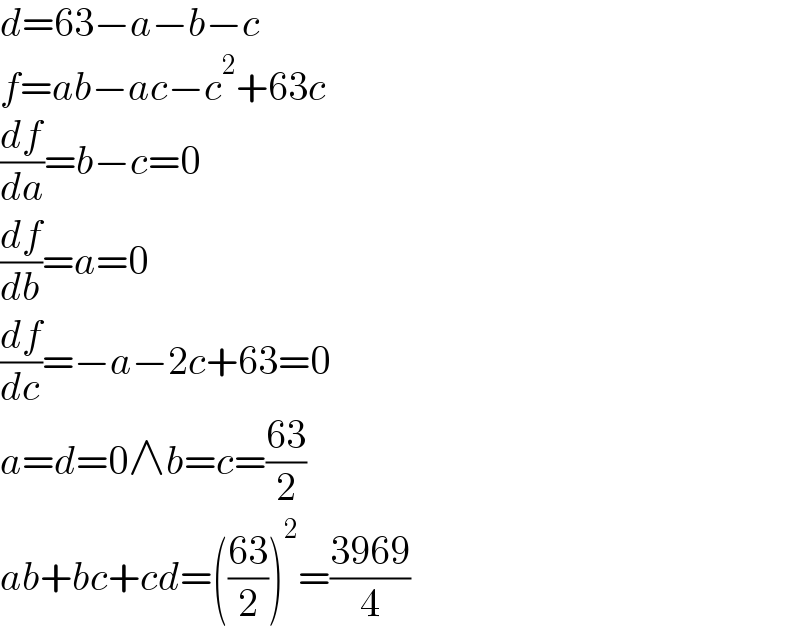
$${d}=\mathrm{63}−{a}−{b}−{c} \\ $$$${f}={ab}−{ac}−{c}^{\mathrm{2}} +\mathrm{63}{c} \\ $$$$\frac{{df}}{{da}}={b}−{c}=\mathrm{0} \\ $$$$\frac{{df}}{{db}}={a}=\mathrm{0} \\ $$$$\frac{{df}}{{dc}}=−{a}−\mathrm{2}{c}+\mathrm{63}=\mathrm{0} \\ $$$${a}={d}=\mathrm{0}\wedge{b}={c}=\frac{\mathrm{63}}{\mathrm{2}} \\ $$$${ab}+{bc}+{cd}=\left(\frac{\mathrm{63}}{\mathrm{2}}\right)^{\mathrm{2}} =\frac{\mathrm{3969}}{\mathrm{4}} \\ $$
Commented by A5T last updated on 05/Nov/24

$${a},{b},{c},{d}\in\mathbb{N}\Rightarrow{ab}+{bc}+{cd}\in\mathbb{N} \\ $$
Commented by Frix last updated on 05/Nov/24

$$\mathrm{Sorry} \\ $$
Commented by Tinku Tara last updated on 05/Nov/24
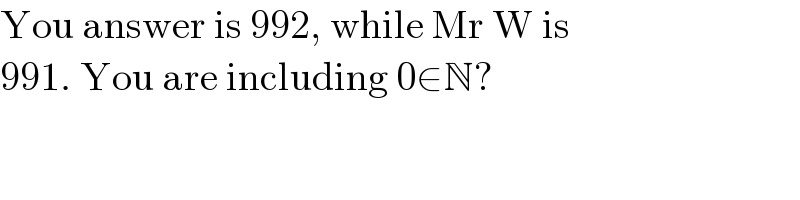
$$\mathrm{You}\:\mathrm{answer}\:\mathrm{is}\:\mathrm{992},\:\mathrm{while}\:\mathrm{Mr}\:\mathrm{W}\:\mathrm{is} \\ $$$$\mathrm{991}.\:\mathrm{You}\:\mathrm{are}\:\mathrm{including}\:\mathrm{0}\in\mathbb{N}? \\ $$
Answered by mr W last updated on 05/Nov/24
![ab+bc+cd=(a+c)(b+d)−ad (ad)_(min) =1×1=1 say (a+c)(b+d)=pq, with p+q=63 [(a+c)(b+d)]_(max) =(pq)_(max) =31×32 ⇒(ab+bc+cd)_(max) =31×32−1=991](Q213424.png)
$${ab}+{bc}+{cd}=\left({a}+{c}\right)\left({b}+{d}\right)−{ad} \\ $$$$\left({ad}\right)_{{min}} =\mathrm{1}×\mathrm{1}=\mathrm{1} \\ $$$${say}\:\left({a}+{c}\right)\left({b}+{d}\right)={pq},\:{with}\:{p}+{q}=\mathrm{63} \\ $$$$\left[\left({a}+{c}\right)\left({b}+{d}\right)\right]_{{max}} =\left({pq}\right)_{{max}} =\mathrm{31}×\mathrm{32} \\ $$$$\Rightarrow\left({ab}+{bc}+{cd}\right)_{{max}} =\mathrm{31}×\mathrm{32}−\mathrm{1}=\mathrm{991} \\ $$
Commented by hardmath last updated on 05/Nov/24
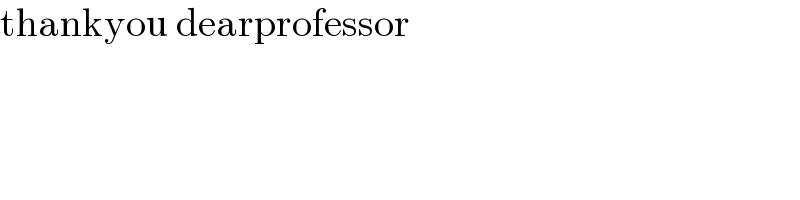
$$\mathrm{thankyou}\:\mathrm{dearprofessor} \\ $$
