Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 215973 by MATHEMATICSAM last updated on 23/Jan/25

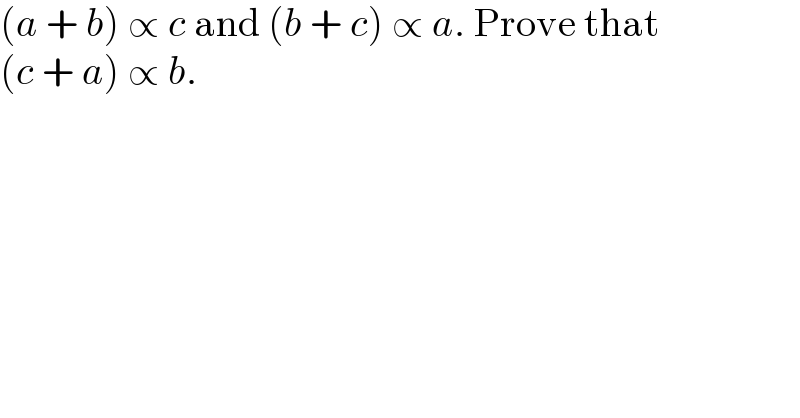
(a + b) ∝ c and (b + c) ∝ a. Prove that (c + a) ∝ b.

$$\left({a}\:+\:{b}\right)\:\propto\:{c}\:\mathrm{and}\:\left({b}\:+\:{c}\right)\:\propto\:{a}.\:\mathrm{Prove}\:\mathrm{that} \\ $$$$\left({c}\:+\:{a}\right)\:\propto\:{b}. \\ $$

Answered by Rasheed.Sindhi last updated on 24/Jan/25

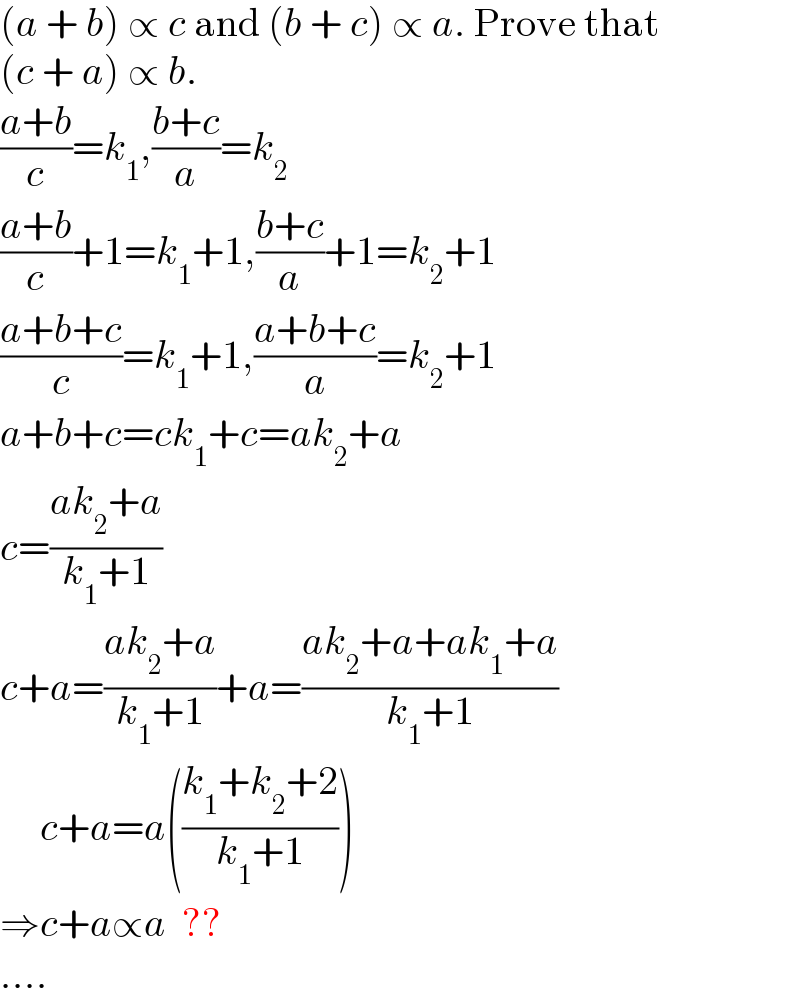
(a + b) ∝ c and (b + c) ∝ a. Prove that (c + a) ∝ b. ((a+b)/c)=k_1 ,((b+c)/a)=k_2 ((a+b)/c)+1=k_1 +1,((b+c)/a)+1=k_2 +1 ((a+b+c)/c)=k_1 +1,((a+b+c)/a)=k_2 +1 a+b+c=ck_1 +c=ak_2 +a c=((ak_2 +a)/(k_1 +1)) c+a=((ak_2 +a)/(k_1 +1))+a=((ak_2 +a+ak_1 +a)/(k_1 +1)) c+a=a(((k_1 +k_2 +2)/(k_1 +1))) ⇒c+a∝a ?? ....

$$\left({a}\:+\:{b}\right)\:\propto\:{c}\:\mathrm{and}\:\left({b}\:+\:{c}\right)\:\propto\:{a}.\:\mathrm{Prove}\:\mathrm{that} \\ $$$$\left({c}\:+\:{a}\right)\:\propto\:{b}. \\ $$$$\frac{{a}+{b}}{{c}}={k}_{\mathrm{1}} ,\frac{{b}+{c}}{{a}}={k}_{\mathrm{2}} \\ $$$$\frac{{a}+{b}}{{c}}+\mathrm{1}={k}_{\mathrm{1}} +\mathrm{1},\frac{{b}+{c}}{{a}}+\mathrm{1}={k}_{\mathrm{2}} +\mathrm{1} \\ $$$$\frac{{a}+{b}+{c}}{{c}}={k}_{\mathrm{1}} +\mathrm{1},\frac{{a}+{b}+{c}}{{a}}={k}_{\mathrm{2}} +\mathrm{1} \\ $$$${a}+{b}+{c}={ck}_{\mathrm{1}} +{c}={ak}_{\mathrm{2}} +{a} \\ $$$${c}=\frac{{ak}_{\mathrm{2}} +{a}}{{k}_{\mathrm{1}} +\mathrm{1}} \\ $$$${c}+{a}=\frac{{ak}_{\mathrm{2}} +{a}}{{k}_{\mathrm{1}} +\mathrm{1}}+{a}=\frac{{ak}_{\mathrm{2}} +{a}+{ak}_{\mathrm{1}} +{a}}{{k}_{\mathrm{1}} +\mathrm{1}} \\ $$$$\:\:\:\:\:{c}+{a}={a}\left(\frac{{k}_{\mathrm{1}} +{k}_{\mathrm{2}} +\mathrm{2}}{{k}_{\mathrm{1}} +\mathrm{1}}\right) \\ $$$$\Rightarrow{c}+{a}\propto{a}\:\:?? \\ $$$$.... \\ $$

Commented by MATHEMATICSAM last updated on 24/Jan/25

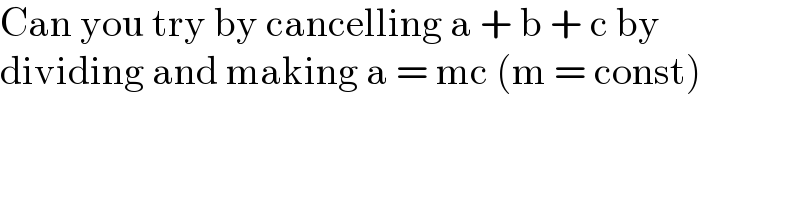
Can you try by cancelling a + b + c by dividing and making a = mc (m = const)

$$\mathrm{Can}\:\mathrm{you}\:\mathrm{try}\:\mathrm{by}\:\mathrm{cancelling}\:\mathrm{a}\:+\:\mathrm{b}\:+\:\mathrm{c}\:\mathrm{by} \\ $$$$\mathrm{dividing}\:\mathrm{and}\:\mathrm{making}\:\mathrm{a}\:=\:\mathrm{mc}\:\left(\mathrm{m}\:=\:\mathrm{const}\right) \\ $$

Commented by Rasheed.Sindhi last updated on 24/Jan/25

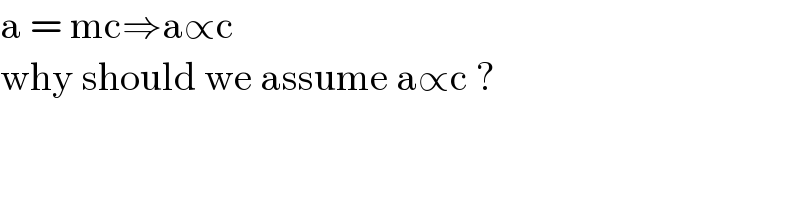
a = mc⇒a∝c why should we assume a∝c ?

$$\mathrm{a}\:=\:\mathrm{mc}\Rightarrow\mathrm{a}\propto\mathrm{c} \\ $$$$\mathrm{why}\:\mathrm{should}\:\mathrm{we}\:\mathrm{assume}\:\mathrm{a}\propto\mathrm{c}\:? \\ $$

Answered by Rasheed.Sindhi last updated on 24/Jan/25

a+b=pc.....(i) b+c=qa....(ii) let c+a=rb ; r is constant.....(iii) (ii)−(i): c−a=qa−pc....(iv) (iii)+(iv) : 2c=rb+qa−pc...(v) (iii)−(iv): 2a=rb−qa+pc....(vi) (v)+(vi): 2c+2a=2rb⇒c+a=rb⇒c+a∝b

$$\: \\ $$$${a}+{b}={pc}.....\left({i}\right) \\ $$$${b}+{c}={qa}....\left({ii}\right) \\ $$$${let}\:{c}+{a}={rb}\:;\:{r}\:{is}\:{constant}.....\left({iii}\right) \\ $$$$\left({ii}\right)−\left({i}\right): \\ $$$${c}−{a}={qa}−{pc}....\left({iv}\right) \\ $$$$\left({iii}\right)+\left({iv}\right)\:: \\ $$$$\mathrm{2}{c}={rb}+{qa}−{pc}...\left({v}\right) \\ $$$$\left({iii}\right)−\left({iv}\right): \\ $$$$\mathrm{2}{a}={rb}−{qa}+{pc}....\left({vi}\right) \\ $$$$\left({v}\right)+\left({vi}\right): \\ $$$$\mathrm{2}{c}+\mathrm{2}{a}=\mathrm{2}{rb}\Rightarrow{c}+{a}={rb}\Rightarrow{c}+{a}\propto{b} \\ $$

Commented by Rasheed.Sindhi last updated on 24/Jan/25

Not sure that the answer is correct

$${Not}\:{sure}\:{that}\:{the}\:{answer}\:{is}\:{correct} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com